

ノイズ対策の考え方と進め方を、
ノイズ対策のポイントとして、10 にまとめました。
◆ 信号 △とは、互いに離れた場所で、光、電気などの符号を用いて、情報をやり取りする方法、またはその符号のことを言います。
そして、符号 △とは、言語、文字またはその他の情報を表現するための記号の体系を言います。
この講座では、信号は電気的な信号を意味します。一般に電気的な信号には、電圧△を使用することが多く、電流△も使用されています。
◆ アナログ △信号では、電圧の大きさが信号であり、大きさの情報を表わします。
ディジタル △信号も、アナログ信号である電圧を利用しています。しかし、ディジタル信号は、ある決められた電圧値よりも、大きいか小さいかによって、0 か 1 かの 2 値情報 △を表わします。
[注1]
上記の表わし方が、最も基本的な、信号の表わし方ですが、別な表わし方も各種使われています。
たとえば、周波数変調△では、周波数△が情報を表わします。
[注2]
ディジタル信号は、2 値でなく、3 値以上の、多値を表わすものもあります。しかし、3 値以上は、ほとんど使われておらず、もっぱら、2 値が使われています。2 値情報は、3 値以上の情報に比べて、その取り扱いが、はるかに、簡単だからです。
◆ 信号はまた、必要な情報を乗せた、(欲しい)信号 と、この(欲しい)信号を妨害するノイズ とに、分けられます(図.1)。
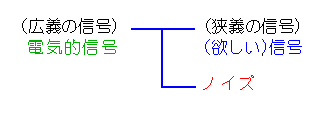
◆ 広義には、信号は、(欲しい)信号とノイズとを合わせたものです。
しかし一般には、狭い意味で使用します。狭義には、(欲しい)信号だけを、信号と呼んでいます。
この講座では、原則として信号は、狭義の信号を指します。とくに広義の意味で使用し、かつそれを明示する必要がある場合には、電気的信号 と呼んで、区別することにします。
◆ ノイズは、一般に、外部から侵入してくると、思われています。もちろん外部から侵入してくるノイズも、主要なノイズです。
しかし、それだけではありません。
信号は、それが伝わって行くうちに、信号の経路に存在する要素によって、歪みます(図.2)。
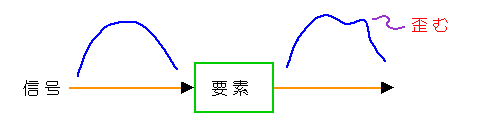
◆ 信号を、意図して歪ませたのであれは、歪んだ結果は、欲しい信号です。意図して信号を歪ませる操作を、信号処理 と呼んでいます。
しかし、意図しない歪みであれば、この信号の歪みは、欲しい信号を妨害するものですから、ノイズの定義に当てはまります。
◆ すなわち、信号が自分自身で歪むことによっても、ノイズが発生します。
しかも、この信号を歪ませる要素は、次の 1.(2-A) に示すように、回路図△には書かれていないことが多いのです。
[注] 信号処理の言葉は、通常は、アナログの信号を、ディジタル信号で表現し、ディジタル技術で処理するという意味で、使っています。ここでは、通常よりも広い意味で、すなわちアナログ信号のままで、処理することを含んで、信号処理の言葉を、使用しています。
◆ 信号やノイズの大きさは、通常パワー(電力)で、表わします。パワー (電力 )(W、ワット)は、単位時間当りのエネルギー量 △(J、ジュール)です。
電力(W) = エネルギー量(J)/時間(s)
しかし、ノイズは、より一般的には、絶対値よりも、信号との比 S/N (信号対ノイズ比)で、表します。

◆ 電力比 は、デシベル (dB )で表わすことができます。
電力比を、対数で表わしたものを、ベル (B) と言います。比ですから、本来、無次元数です。しかし、多く用いられるので、とくに単位名称△を付けて ベルと呼んでいます。
通常は、ベル (B)を 1/10 にした単位、デシベル(dB)が使用されています(単位が 1/10 ですから、数値は 10 倍になります)。
◆ デシベルは、電圧比 にも使用されます。ただし、電圧比の場合には、
ベル = 20デシベル
です。
これは、電力を P、電圧を V、抵抗 R としたとき、抵抗 R で消費する電力と抵抗に掛かる電圧との関係が、
P = V2/ R
の関係にあるからです。ベルの定義は、電力比ですから、電圧比を、ベルで表すときは、電力比に換算しているのです。2 乗は対数では 2 倍になります。
◆ このように、ベルは、電力のときと電圧のときとで、違いがあることに注意してください。電流比も、電圧比と同様に、
ベル = 20デシベル
です。
◆ 以上のように、S/N は、電力比で定義されます。しかし、信号は、電圧を利用して、その大きさを表わしたり、伝えることが多いので、信号やノイズを、電圧や電圧比で評価した方が適切なことも、多いのです。
◆ 信号を歪ませる要素は、何らかの回路素子 です。意図した、信号処理を行なうためには、それに適合した、回路素子(たとえば、抵抗△やコンデンサ△)を使用します。
この回路素子は、ちゃんと回路図 △に載っています。
ところが、ノイズを発生させる回路素子は、通常は、回路図のどこを探しても載っていないことが多いのです。
◆ しかし、回路図に載っていないだけであって、波形を歪ませる要因は、厳として存在します。
回路図に記載されている回路素子は、理想的に動作するものとして、表わされています。
回路図では、抵抗は、理想的(純粋)な抵抗であり、コンデンサは、理想的(純粋)なコンデンサです。
しかし現実に使用されている素子は、理想から外れた特性、すなわち、現実特性 を持っています。
◆ 図.3は、素子の理想特性 と現実特性とを、回路図の形と、周波数特性 △の形で示したものです。
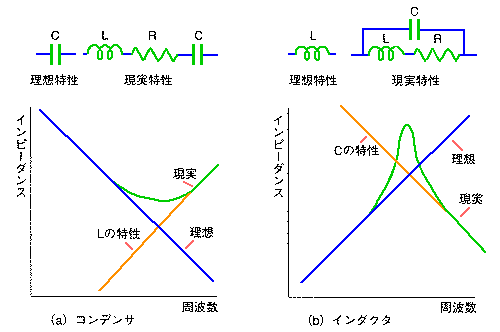
◆ 図から分かるように、周波数が低い範囲では、素子は、ほぼ理想どおりに動作しますが、周波数が高くなると、その現実特性は、理想特性から、大きく隔たってしまいます。
素子を選定するときは、その素子が使用する、信号の周波数帯域で、ほぼ理想的に働くように、素子を、選定します。したがって、その素子を、その使用目的に使用する、周波数の範囲では、ほぼ、理想どおりに動作します。
◆ しかし一般に、ノイズは、信号よりも高周波です。素子が、信号の周波数帯域では、ほぼ理想どおりに動作しても、ノイズの周波数に対しては、理想特性から大きく隔たってしまう可能性があります。
図に示すように、周波数が高いところでは、コンデンサはインダクタ △に、化けてしまいます。ノイズをフィルタ △で取り除こうとしたのに、この現実特性のために、フィルタできないかも知れません。
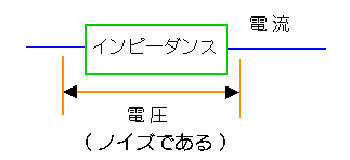
◆ 信号線 は、回路図の上では、インピーダンスゼロの理想特性を持っています。
しかし現実の信号線は、必ずインピーダンス△を持っています(図.4)。
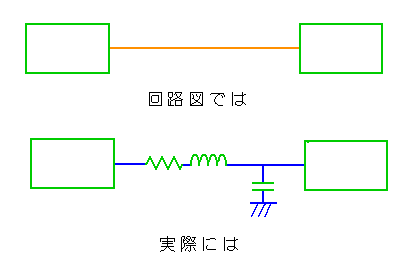
◆ インピーダンスに電流が流れれば、電圧が発生します(図.5)。この電圧はノイズです。
◆ このインピーダンスがインダクタンスのときは、インピーダンスの値は、jωL です。電流の周波数(ω)が高いと、インピーダンスは大きな値となり、大きな電圧、すなわち大きなノイズが発生します。
一般に信号線の抵抗は十分に低いですから、抵抗による電圧は無視できます。
しかし、高周波のノイズ電流に対しては、インダクタンスにより発生する電圧を無視することは、できません。
[注]
真直ぐな普通の信号線も、インダクタンスを持っています。線を環状に巻くと、大きなインダクタンスを持ちます。とくにインダクタンスが大きくなるように作ったものがコイル △です。
同様に、普通の信号線は、キャパシタンスを持っています。コンデンサは、とくにキャパシタンスが大きくなるように作ったものです。
◆ このように、回路図には書いてなくても、現実には存在する回路のことを、回路図に無い回路 と呼んでいます。
ノイズ対策では、この回路図に無い回路を考えることが必要であり、重要なのです。
★ 信号には、いろいろあります。モールス符号も、信号の一種です。見てきれいな信号は、信号旗です(下図左)。旗を使った信号には、手旗信号もあります(下図右)。


★ さて、電気的信号には、直流と交流とがあります。直流 △は、(それを考えている期間)一定な信号です。これに対して交流 △は、電流の流れの方向が変化する信号です。
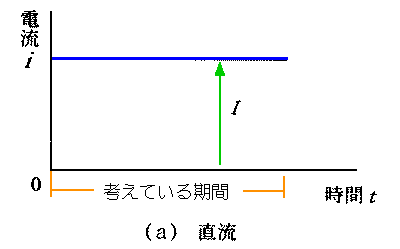
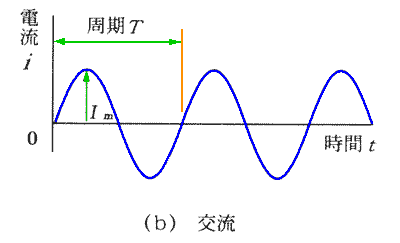
図は、電流の波形ですが、電圧の波形も同様です。
★ 交流とは、平均値がゼロで、プラス側とマイナス側が対称な波形のことをいいます。図は、交流の代表である正弦波形です。正弦波形 は、式では、
i = sin (ωt)
で表わされます。
ω を角速度 といい、周期 T に対して、
ω = 2π / T
の関係があります。また、周波数 f は、
f = 1 / T
であり、その単位は Hz (ヘルツ )です。
★ 正弦波形の交流、正弦波交流 は、最も代表的な交流で、単に交流という場合、通常は正弦波交流を指します。
しかし、交流は正弦波交流には限定されず、上記の定義に従うものは、全て交流です。下図は、交流のいろいろです。
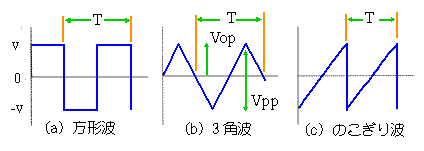
[注] 正弦波形は、上に示したような性質だけでなく、位相 △を考える必要があります。
★ さらに一般的な信号は、単なる交流ではなく、複雑に変化する任意波形の信号です。
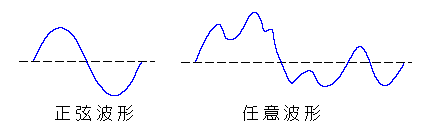
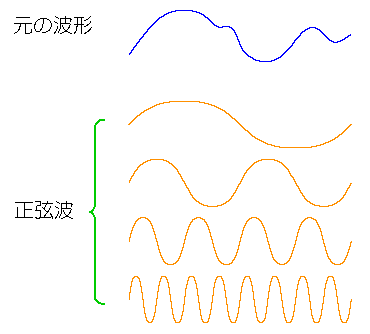
★ 任意波形の信号は、直流成分と、多数の(互いに周波数が異なる)正弦波形の集まり(加算)で、表わすことができます。
★ ある信号に、どの周波数の成分が、どのような割合で含まれているかを示したものを、その信号の周波数特性 といいます。
ある信号に含まれている周波数(f)には、上限と下限があります。その信号に含まれている周波数の範囲を、その信号の周波数帯域 (帯域幅 、帯域)といいます。周波数帯域は、絶対値(Δf)で表すこともありますが、多くは、信号の周波数に対する割合(Δf/f)で表します。
★ また、素子や、素子の集まりである回路は、その入力と出力との間で、どの周波数の成分をどのように変化させるかの特性が決まっています。
これを、その素子や回路の周波数特性 と呼んでいます。
周波数特性は、このように、2 つの意味を持っています。
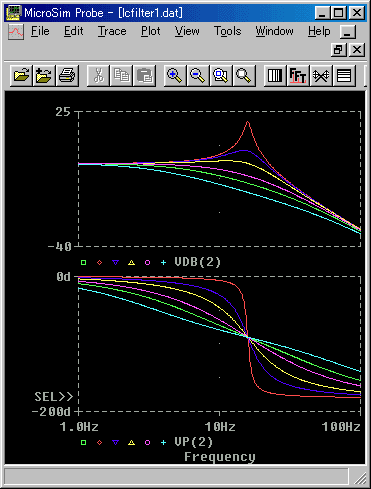
★ 周波数特性は、通常、横軸を周波数の対数にとり、縦軸(振幅 )は dB で目盛ります。周波数特性の 1 例を示します。図は、LC フィルタと呼ばれるフィルタ△の周波数特性です。LC フィルタは、Q △と呼ばれる定数の値によって、その特性が変化しますから、いろいろな特性のものを、示してあります。
★ 抵抗 (記号 R)は、電気の流れを制限する素子です。ただし、厳密には、抵抗ではなく、電気抵抗です。単に抵抗というと、電気抵抗以外にも、いろいろあります。政治の流れに掉さすのは、抵抗勢力です。
★ 水などの流体にも抵抗があります。流体の抵抗は、電気抵抗よりも複雑です。流速によって、抵抗値が、変化するからです。管路中の流体抵抗は、流速が低いときは、流速に比例しますが、流速が速くなると、流速の 2 乗に比例します。
★ 3 次元の空間では、さらに複雑です。抵抗は、物体の形状に依存します。空気中では、いわゆる「流線形」が、優れています(下図上)。しかし低速の水中では、先端が丸く後尾が先細りの形状の抵抗が低くなります(下図左下)。高速では、先端が尖り、後部は流線形ものが優れています(下図右下)。



★ さて、抵抗を R、抵抗の両端に掛かる電圧を V、抵抗を流れる電流を I とすれば、次のオームの法則 が成立します。
★ オームの法則は、直流、交流の両方で成立します。ただし、交流の場合は、実効値を使用します。実効値 とは、電力が直流と等価となる値のことです。
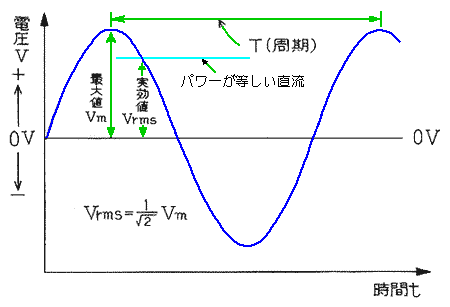
★ 正弦波形では、実効値 Vrms は、振幅(最大値)を Vm として、
Vrms = Vm / √2
です。
★ コンデンサ は、電荷を蓄える能力を持った素子です。電荷の量(電気量)を Q、コンデンサのキャパシタンス (静電容量 )をCとすれば、
C = Q / V
です。電流は、単位時間当りの電荷の移動量ですから、C V = Q を時間で微分して、
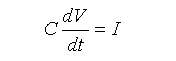
となります(理想特性)。微分方程式になっています。これを解くと、
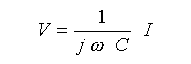
となります。ここで、j は虚数 (-1 の平方根)△です。数学では、虚数を i で表わしましが、電気では電流の i とまぎれるので j を使用しています。ω は信号の角速度です。
★ 角速度 ω は、信号の周波数を f とすれば ω=2πf (πは円周率)であり、角速度は周波数に比例します。
角速度は、周波数ではありませんが、周波数と比例関係であるため、周波数と同じ意味に用いられています。こにため、周波数を、角速度を単位として表わす場合があり、これを角周波数 と呼びます。
★ (1/jωC)=Z と置けば、
となり、オームの法則と同様な関係が成立します。Z は抵抗 R に相当する定数です。ただし、上の式から分かるように、交流の周波数によって値が変化します。すなわち、周波数特性があります(コンデンサの周波数特性は△)。
★ この定数 Z を、コンデンサのインピーダンスと言います。
すなわち、インピーダンス △は、直流の抵抗を交流に拡張した概念です。
★ 抵抗の測定において、測定の対象が電解質を含むときは、直流で測定すると、電池作用のために、大きな誤差を生じます。これを防ぐために、交流を使用して、そのインピーダンスを計ります。たとえば、ラットの発情期の判定に使用するラット用膣インピーダンスチェカは、実質的には抵抗を測りたいのですが、交流でインピーダンスを計っています。

★ なお、抵抗は、交流に対しても周波数特性はフラットであり、インピーダンスは、周波数によって変化しません。
★ インダクタ(コイル、記号 L)△(理想特性)は、直流抵抗はゼロですが、交流に対しては電気の流れを制限します。インダクタのインダクタンスを L とすれば、
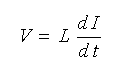
であり、これを解くと、
V = j ω L I
となり、(jωL) が、インダクタのインピーダンスです。その周波数特性は、コンデンサとは逆になります(インダクタの周波数特性は△)。
★ 抵抗、コンデンサ、インダクタが複合した回路(たとえばフィルタ)も、インピーダンスを持ちます。その周波数特性は、複雑です。
コンデンサは電界、インダクタは磁界の作用を利用した素子です。コンデンサは、電界の形で、エネルギーを蓄えます。これに対して、インダクタは、磁界の形でエネルギーを蓄えます。コンデンサやインダクタは、エネルギー△を蓄える素子です。これに対して、抵抗は、エネルギーを消費する素子です。
★ トランスは、2つのインダクタが、磁界によって互いに結合したもので、一方から他方に電圧を伝えます。この相互の結合は、インダクタンスで表わされ、相互インダクタンス といいます。
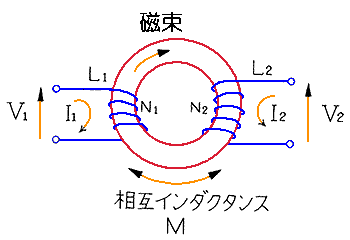
★ 負荷抵抗を接続した状態では、
V1 = jω L1 I1 + jω M I2
V2 = jω L2 I2 + jω M I1
が成立します。また、
V1 / V2 = N1 / N2
I1 / I2 = N2 / N1
となります。
★ なお、微分方程式をインピーダンスの形に変換する過程、インピーダンスの表現方法、周波数特性などに関しての詳細は、
自動制御WEB講座「3.1.1.(4)、3.1.1.(5)、3.1.2.(2)、3.1.2.(3)」を参照してください。
なお、周波数特性のことを、自動制御では周波数応答と呼んでいます。同じものです。
◆ 外来ノイズは、必ず伝わってくる経路が存在します。
この経路が、回路図に無い回路になっていることが多いのです。
2本の信号線が、平行している場合を考えます(図.6)。
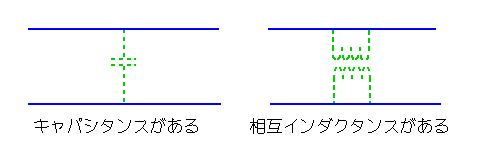
◆ 2本の線が互いに独立であれば、電気的信号、したがって、ノイズは伝わってこないはずです。
しかし、2本の線が平行して走っていれば、その間には、ストレキャパシタンス(浮遊容量)が存在します。このストレキャパシタンスを介して、ノイズが伝わります。回路図に無い回路としてのキャパシタンスは、随所に存在します。これをストレキャパシタンス △と呼んでいます。
◆ また、平行して走る、2 本の線の間には、相互インダクタンスがあり、相互インダクタンスによっても、ノイズが伝わります。
[注] 互いに直交する信号線の、キャパシタンスや相互インダクタンスは、平行する線に比べれば、無視することができます。
◆ さらに、信号は、空中を電波(電磁波)の形で伝わります。電波は、電界と磁界とが総合されたものです。
アンテナは、空中に電波を発射します。これを放射といいます。アンテナはまた、空中の電波を取り込みます。
電気の導体は、アンテナ作用を持っています。
距離が離れているときでも、相互にアンテナになることによって、放射を介して、ノイズが伝わります。
◆ これらは、何れも回路図には書いてありません。すなわち、ノイズは、回路図に無い回路を通って伝わります。
もちろん、信号と共に、信号線を伝わるノイズもあります。