

◆ コイル L とコンデンサ C とを組み合わせた、LC フィルタ があります(図 3.2-16)。LC フィルタは、リアクタンスが 2 つですから、2 次フィルタですが、RC 2 段の段重ねの 2 次フィルタよりも、優れた特性を持たせることができます。
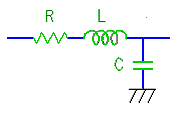
◆ LC フィルタは、名前の上からは、L と C ですが、実用上は、さらに、抵抗 R を加えて考える必要があります。コイル L は、現実特性として、抵抗 R の成分を持っています。この現実特性としての抵抗 R の成分は、無視することができません。また、LC フィルタに欲する周波数特性を持たせるためには、故意に抵抗 R を付加することが必要です。このどちらかの理由から、LC フィルタは、図のモデルを、使用することにします。
LC フィルタの周波数特性を、図 3.2-17 に示します。比較のために、RC 2 段重ねフィルタの特性も入れてあります(緑)。
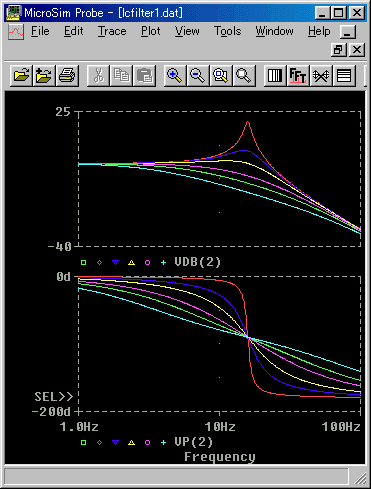
◆ LC フィルタは、2 次フィルタですから、阻止域の、減衰は-40dB/dec、位相差は-180°です。周波数特性は、フィルタの直列抵抗 R の大きさによって、大きく変化します。抵抗 R が大きいときは、振幅比、位相差ともに変化は緩やかで、RC 2 段重ね(図の緑)よりも、緩くなる条件も、あります(図の水)。抵抗 R が小さくなると、シャープな変化が生じます。図で、R = 0.1、0.5 のときには、ピークができます。このように、周波数特性の振幅比に、ピークができる現象を、共振 といいます。
◆ 共振が起こる原因を調べてみましょう。インダクタンス L、キャパシタンス C の直列インピーダンスは、
![]()
です。したがって、ω2 L C = 1 のとき、すなわち、
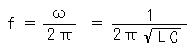
のとき、L と C との直列インピーダンスがゼロになり、ピークを作ります。ただし、f は、周波数です。
これが、共振の条件です。すなわち、共振周波数 は、上記の値であり、そのときのインピーダンスは R です。
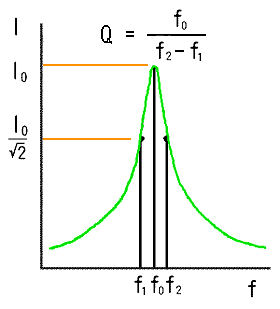
◆ 共振の鋭さは、Q (クオリティファクター )と呼ばれる値で、示されます(図 3.2-18)。Q は、ピークの高さの 1/√2 のところの幅 (f2 - f1) で、ピークの周波数 f0 を割ったものです。
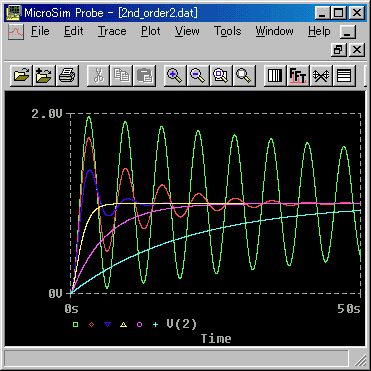
◆ LC フィルタの、過渡特性を図 3.2-19 に、さらにこの過渡特性の、立ち上がり部分の拡大を、図 3.2-20 示します
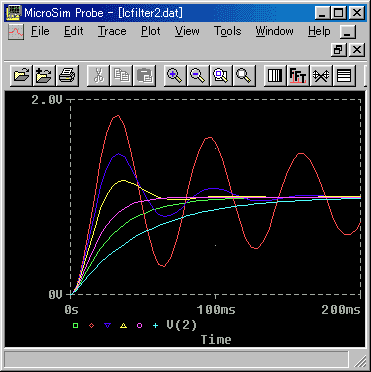
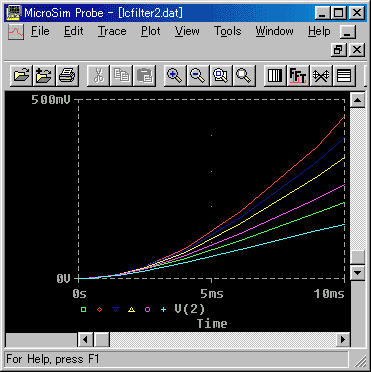
◆ 2 次フィルタですから、立ち上がりの最初の部分は、
水平です。
抵抗 R が小さくて、周波数特性がピークを作っている条件では、過渡特性の波形が、振動的になっています。抵抗 R が大きくなると、波形は、非振動的になります。共振とは、過渡特性において、波形が振動することです。その条件が、周波数特性では、振幅にピークを作ることであった訳です。
図には示してありませんが、そしてパッシブフィルタでは、現実には起こりませんが、抵抗 R がゼロになると、振動は、減衰しないで振動し続けます。このときは、周波数特性の共振のピークは、無限大になります。
この抵抗 R がゼロになるという条件は、アクティブフィルタのときには、実現することができます。
◆ 図で、R = 1のときは、落ち着く値を一旦上回ってから落ち着いています。このような波形を行き過ぎ といいます。
フィルタの過渡特性の波形においては、行き過ぎを許容するときと、許容しない場合とがあります。行き過ぎを許容するときは、R = 0.5 程度の波形が、早く立ち上がる、という意味で、適切と考えられます。行き過ぎを許容できないときは、R = 2 の波形が良いでしょう。
◆ LC フィルタも、段重ねにしてみましょう(図 3.2-21)。図の特性は、R = 0.1 で、共振がある条件です。
[図 3.2-21] LC フィルタの段重ねの周波数特性(R = 0.1)
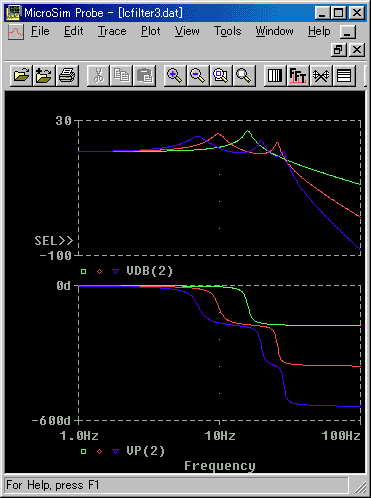
◆
RC フィルタは、1 次フィルタですから、それを n 段重ねると、n 次フィルタになりました。LC フィルタは、2 次フィルタですから、その n 段重ねは、2n 次フィルタになります。したががって、阻止域の減衰は、180 × n °/ dec です。RC フィルタと比べて、特性が、大幅に改善されています。
振幅比は、1 段のときには、1 つの共振周波数であったのが、2 段重ねでは、2 つ、3 段重ねでは 3 つに、ピークが増えています。これは、段重ねしたことによって、後段が、前段に影響しているからです。後段が前段に影響するという点では、RC フィルタの段重ねと同様ですが、LC フィルタの方が、波形が複雑になっています。
ローパスフィルタとして使用するときは、ピークが無い方が好ましい訳ですから、ピークが発生しない条件を、調べてみましょう。図 3.2-22 は、LC 1段のときに適切だった条件(R = 1)での特性です。
[図 3.2-22] LC フィルタの段重ねの周波数特性(R = 1)
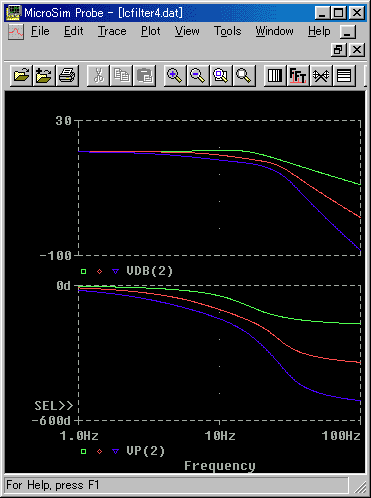
◆ 段重ねによって、通過域が、だれてしまいました。そこで、図 3.2-21 との中間(R = 0.4)を取ってみたのが、図 3.2-23 です。
[図 3.2-23] LC フィルタの段重ねの周波数特性(R = 0.4)
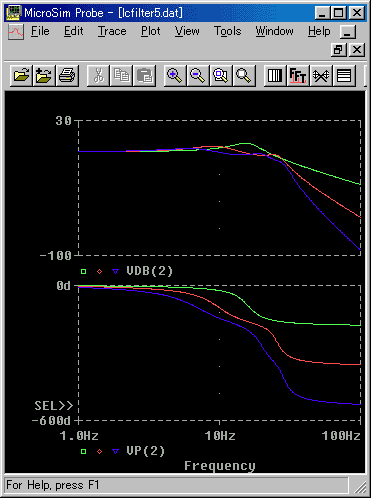
◆ ほぼ適切と思われるフィルタ特性が、得られています。
★ RC フィルタや、LC フィルタなど、各種のフィルタについて説明してきました。説明したのは、フィルタ単体の特性です。
パッシブフィルタを考えるときには、フィルタの信号源と負荷について考える必要があります。
★ 負荷は、「ふか」ですが、「おいに」とも読み、背負った荷物のことです。

★ フィルタは、最初に定義したように、「ある回路を通過させることによって、その入力と出力との周波数特性を変化させる回路」です。
したがって、フィルタは、フィルタの入力である、信号源 と、フィルタの出力である、負荷 とに挟まれた位置にあります。フィルタの入力である、信号源は、さらに、電圧源 Vs と信号源インピーダンス Zs とに分けられます。
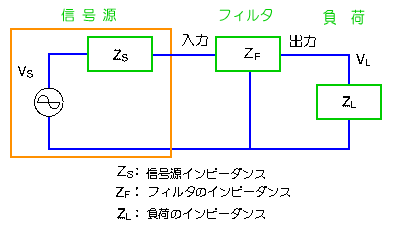
★ 本文で、これまで調べてきた、フィルタの特性は、電圧源 Vs が定電圧源、信号源インピーダンス Zs がゼロ、負荷インピーダンス ZLが無限大という、理想特性です。しかし、現実には、電圧源 Vs が定電圧源であるとは限りません。定電圧源であったとしても、信号源インピーダンスは、無視できない場合があります。負荷も無限大とは、みなせないことがあります。このような、条件のときを、調べて見ましょう。
★ 信号源インピーダンスや負荷インピーダンスは、インピーダンスと称していますが、実際には、抵抗の場合がほとんどです。したがって、信号源抵抗 、負荷抵抗 の言葉も用いられています。以下は、インピーダンスを抵抗に限定して、説明します。
フィルタは、理想的な LC フィルタ(図 3.2-16 において、R = 0)を考えます。
★ (1) 負荷インピーダンス ZL = ∞ で、信号源インピーダンスが、抵抗 R のときは、図 3.2-17 と同じです。図 3.2-16 の R を、信号源インピーダンスと読み替えれば良いわけです。両方を共に考える必要があるときは、両者を加算した値で読み替えます。
実際には、信号源インピーダンスは、低い場合が多いでしょう。したがって、フィルタ単体の特性と、あまり変わりません。しかし、ときには、信号源インピーダンスが高いときもあります。このようなときには、フィルタの特性は、ゆるくなります。
★ (2) 負荷インピーダンスの影響を、見てみます(下図)。負荷が小さくなれば、特性は緩やかになります。その傾向は、信号源インピーダンスのとき(図 3.2-17)と、ちょうど逆になります。なお、図で、ZL = 1MEG は、実用上、負荷無限大を意味します。
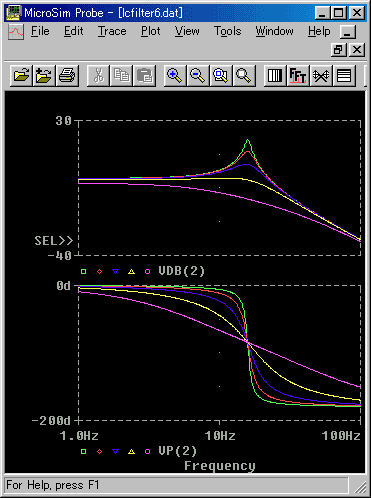
★ 以上、フィルタが、信号源と負荷とに挟まれているケースについて考えてきましたが、さらに一般化すると、フィルタは、フィルタの入力 と出力 とに挟まれています。
★ フィルタを入力側から見たインピーダンスを、入力インピーダンス 、フィルタを出力側から見たインピーダンスを、出力インピーダンス といいます。
これらの、インピーダンスは、抵抗であることが多く、抵抗のときは、入力抵抗 、出力抵抗 と、呼んでいます。
★ なお、この入力インピーダンス、出力インピーダンス、信号源、負荷などの言葉は、フィルタに限らず、広く一般に、使われている用語です。

★ さて、フィルタの入力インピーダンスが、大きいということは、フィルタの入力側に接続されている回路が、フィルタを接続したことによって受ける、影響が小さい、ということです。フィルタの出力インピーダンスが、小さいということは、フィルタの出力側に接続されている回路によって、フィルタが影響を受けることが少ないことを、意味します。
★ すなわち、入力インピーダンスは大きいことが良く、出力インピーダンスは小さいことが望ましいわけです。しかし、パッシブフィルタは、この条件を満足しません。この条件を満たすのが、アクティブフィルタです。
◆ LC フィルタも、伝達関数で表すことができます。しかし、ここでは、LC フィルタを含み、2 次フィルタを一般化した、下記の形の伝達関数を調べてみましょう。その周波数特性は、図 3.2-24です。
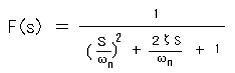
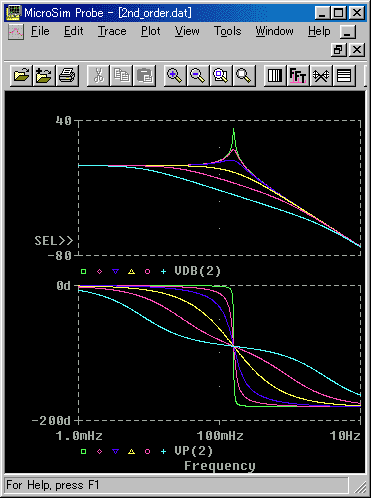
◆ ここで ζ は、2ζ= 1/Q の関係があります。この ζ のことを、減衰定数 といい、ζ = 1 が、系が振動するかどうかの境界です(図 3.2-25)。すなわち、ζ > 1 のとき非振動的、ζ < 1 のとき振動的になります。図には示してありませんが、ζ = 0 のときは、非減衰の持続振動 になります。振動しても振幅が減衰するときは、減衰振動 です。
◆ 伝達関数の分母をゼロと置いた方程式のことを、特性方程式といいます。2 次フィルタの特性方程式は、2 次方程式です。
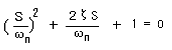
ζ > 1 のときは、因数分解することができます。この場合には、2 つの 1 次フィルタの合成になります(図 3.2-26)。ζ = 1 のときは、等根です。
[図 3.2-26] 2 次フィルタ( ζ ≧ 1 のとき)
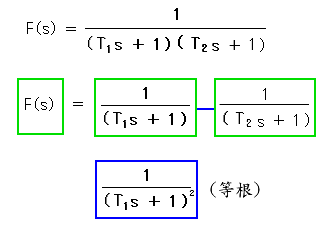
◆ ζ ≫ 1 のときは、2 つの 1 次フィルタの時定数の差が大きいので、周波数特性の上でも、2 つの 1 次フィルタが合成されていることが、読み取れます(図で ζ = 10 のとき)。
◆ ハイパスフィルタ は、要するに、ローパスフィルタの逆です。簡単に紹介します。最も簡単には、抵抗 R と、キャパシタンス C との組み合わせで作ります(図 3.2-27)。これは、1 次フィルタで、CR フィルタ と呼ばれています。この例のように、2 素子で作るフィルタは、入力側の素子を先に書くことによって、フィルタの構成を明示することができます。
◆ 周波数特性を、図 3.2-28 に示します。図には、比較のために、ローパスフィルタの特性を入れてあります。
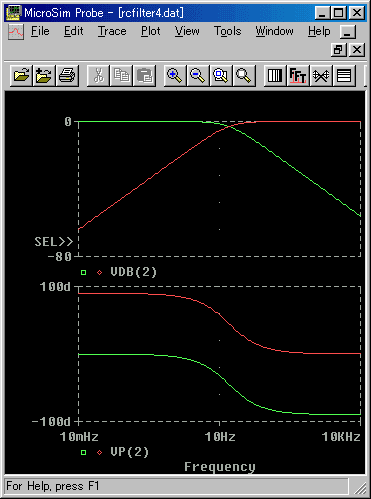
◆ ハイパスフィルタは、ローパスフィルタに対して、振幅比は、横軸(周波数)方向に、鏡面対称になっています。位相差は、ローパスフィルタが、低周波で 0°高周波で -90°であるのに対して、ハイパスフィルタは、高周波で 0°低周波で+90°になっています。
位相が 90°進んでいるということは、微分を意味します。逆に、位相が 90°遅れているということは、積分を意味します。
◆ すなわち、ハイパスフィルタは、低周波領域では、微分特性を持っています。このように、部分的に微分の特性を持っていることから、1 次ハイパスフィルタのことを、不完全微分 ともいいます。ローパスフィルタは、高周波領域で、積分特性を有します。したがって、1 次ローパスフィルタの別名は、不完全積分 です。
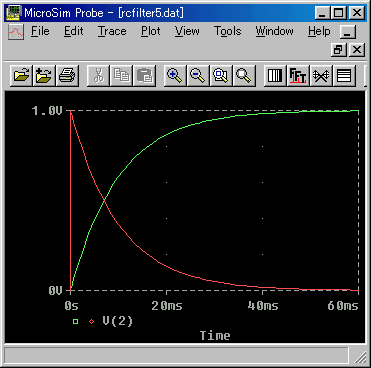
◆ ハイパスフィルタの過渡特性を、図 3.2-29 に示します。これも、比較のために、ローパスフィルタを入れてあります。ハイパスフィルタでは、図のように、最初に立ち上がりのピークがあります。
★ ローパスについては、コラム 3.2-7で紹介しました。ここでは、先ず、ハイパスについてです。ハイパスには、峠などの「切通しの道」の意味があるようです。これは、鎌倉の極楽寺坂切通しです。

★ オーディオでは、音質が重要です。オーディオの周波数特性は、基本的には、低音から高音まで、広い周波数帯域にまたがって、フラットな特性であることが、要求されます。アンプの周波数特性は、比較的容易に所定の特性のものが作れます。スピーカの周波数特性が、重要です。
★ 高性能のオーディオでは、低音から高音までを、1 つのスピーカで賄うことは、できません。低音用スピーカのウーファと高音用スピーカのトウイ-タとを併用します。このとき、オーディオ信号を、低音と高音とに分割して、スピーカに供給する必要があります。これを、実現するのが、クロスオーバーネットワークです。
★ クロスオーバーネットワークは、ローパスフィルタとハイパスフィルタとの組み合わせです。

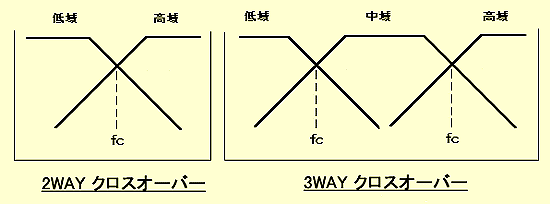
★ 上図で、3WAY クロスオーバーというのは、ウーファに加えて、さらに低音用に、サブウーファのスピーカを使用した、3 つのスピーカを使う方式です。図から分かるように、低域用がローパスフィルタ、高域用がハイパスフィルタです。3WAY クロスオーバーの、中域用は、バンドパスフィルタです。
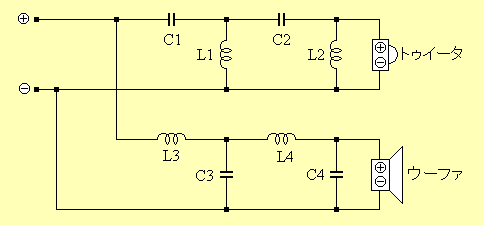
★ フィルタには、いろいろなものが使用されますが、2WAY クロスオーバー用の、シャープな特性を持ったものの 1 例を示します。ローパスフィルタは、LC フィルタの 2 段重ねです。ハイパスフィルタは、キャパシタンス C とインダクタンス L の順序が逆ですから、CL フィルタです(3.2.(2-D))。その CL フィルタ の、2 段重ねになっています。
★ ハイパスフィルタとローパスフィルタは、観測データの処理にも利用されています。地震計の記録解析に利用した例を示します。
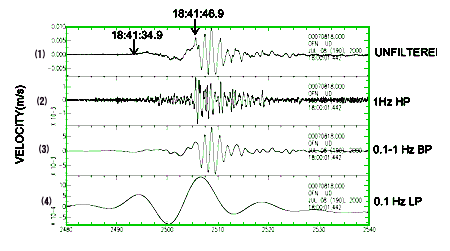
★ 図で、(1)は元の観測データ、(2)はハイパスフィルタで 1 Hz 以上の振動を抽出した波形、(3)はバンドパスフィルタで 0.1 〜 1 Hz を、(4)はローパスフィルタで 0.1 Hz 以下を分離した波形です。フィルタを掛けた波形を見ることによって、単に元波形を眺めるよりも、多くの情報が得られます。
★ 観測波形などの、波形の周波数特性を求める測定機に、スペクトラムアナライザ があります。波形の詳細な周波数特性を求めるときは、スペクトラムアナライザを使用します。しかし、このような、荒分けの方が、分かりやすい情報を提供してくれる場合があります。