

◆ この、お話では、インピーダンスよりも、広い概念である、伝達関数を導きました。伝達関数を使えば、一般波形を取り扱うことができます。しかし、電気では、交流を取り扱うことが、圧倒的に多いのです。取り扱うのは、正弦波形とは限りません。しかし、正弦波形で無くても、多くは、正弦波形の集まりです。したがって、周波数特性を利用することができます。任意関数を取り扱うことができる、伝達関数を使用しなくても、伝達関数よりも、狭い概念である、インピーダンスで、用が足りることが、多いのです。
以降、インピーダンスと、その関連の技術について、解説します。
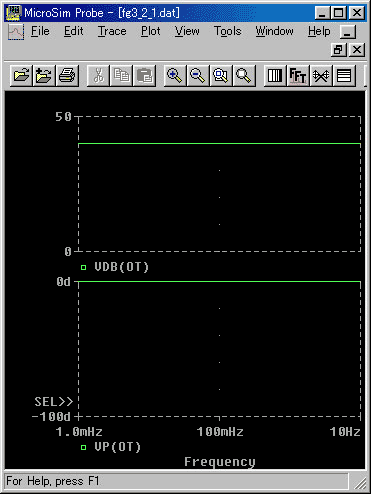
◆ 抵抗 R のインピーダンスは、R そのものです。周波数特性は、フラットです(図 3.2-1)。図は、回路シミュレーションによる波形です(回路シミュレーションは、コラム 3.2-1参照)。回路シミュレーションによって作った波形は、オッシロスコープ(コラム 3.2-2 参照)の観測波形と、ほぼ同様に見ることができます。ただし、この図は、周波数特性の図ですから、通常のオッシロスコープの波形ではなく、ボード線図の形で示されています。横軸は周波数(対数)、縦軸は、上が振幅比で[ dB]、下が位相差で[ °] です。
◆ 入力を電流、出力を電圧とする、コンデンサ C の周波数特性を、図 3.1-2 に示します。コンデンサ C の伝達関数 FC(s) は、FC(s) = 1 / C s です(3.1.(2-B-b))。したがって、コンデンサのインピーダンスは、1 / jωC となります。
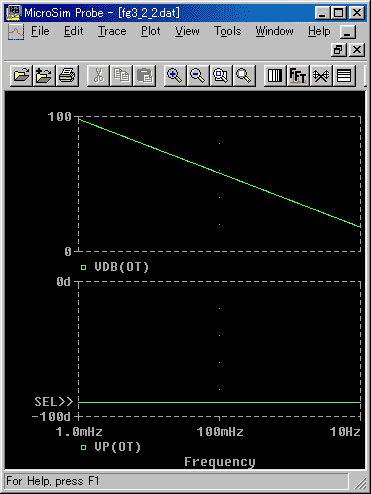
◆ 振幅比は、直線になっています。振幅比の大きさは、周波数に反比例しています。横軸の周波数と、縦軸の振幅比が、ともに、対数なので、直線になったのです。このボード線図は、縦軸と横軸のスケールが等しくありませんが、スケールが等しければ、傾斜が 45°の直線になります。
位相は、-90°で一定です。
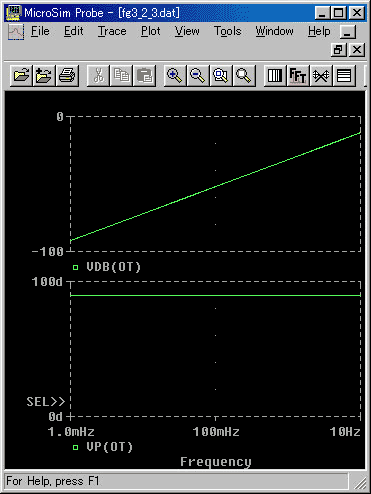
◆ 入力を電流、出力を電圧とする、インダクタ L の伝達関数は、インダクタンスの定義から、 FL(s) は、FL(s) = L s です。したがって、インピーダンスは、jωL で、周波数特性は、図 3.2-3 です。コンデンサとは、ちょうど逆の特性に、なっていることが、分かります。
★ 回路の特性は、回路図や、インピーダンス、さらには伝達関数によって、知ることができます。しかし、式の形では、直感性がありません。直接波形の形で見るのが、最も直感的です。代表的な、応答波形は、過渡特性と、周波数特性です。すでに述べたように、一長一短がありますから、目的と用途によって、使い分けます。
★ これらの波形は、実際に回路を組んで、動かしてみれば、得られます。しかし、実際に回路を組んで動かすのには、手間も、費用も掛かります。
実際に回路を組んで動かす代わりに、パソコン上の、シミュレーション (模擬実験)によって、波形を見ることができます。これを、回路シミュレーション と呼び、そのプログラムを、回路シミュレータ といいます。
★ この講座で使用している回路シミュレータを簡単に紹介します。
回路を記述したプログラムを回路ファイルといい、回路ファイルを作成して、回路シミュレータで実行します。
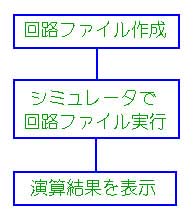
★ このシミュレータでは、回路ファイルを、回路図の形でなく、伝達関数の形で記述することができます。そして、この伝達関数の形で記述された回路ファイルから、過渡特性、周波数特性の、どちらも求めることができます。
すなわち、回路シミュレーションを利用すれば、回路は、全て伝達関数の形で記述しておけば良いわけです。ただし、伝達関数の形で表すことができない回路もあります。
★ 伝達関数の形で記述した回路ファイルの例を示します。この回路ファイルは、図 3.2-1 のものです。
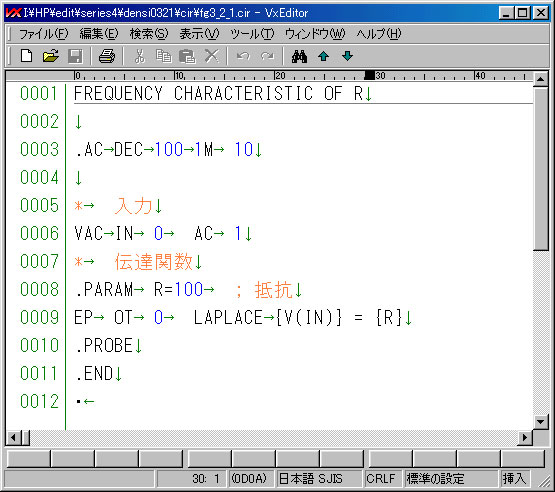
★ 説明はしませんから、こんなものだということで、眺めてください。
なお、回路シミュレータについての詳細は、別の講座「自動制御の基礎と実際」にあります。回路シミュレータ自体について、詳細を知りたい人は、そちらを参照して下さい(自動制御の基礎と実際「まえがき 6」、「2.1 シミュレータの使い方」)。
★ オッシロスコープ は、電気的な現象を、波形として観測する、計測器で、最もポピュラーな計測器の 1 つです。以前は、シンクロスコープ と呼ばれていたこともありますが、同じものです。

★ オッシロスコープは、波形観測が目的ですから、元々は、アナログ計測器です。しかし、最近は、ディジタル化した、ディジタルオッシロスコープ (ディジタルオッシロ )が多くなっています。
先ず、本来のアナログオッシロスコープについて、説明します。オッシロスコープの表示部は、テレビでも使っている、CRT ディスプレイ (ブラウン管 )です。オッシロスコープの構成を示します。
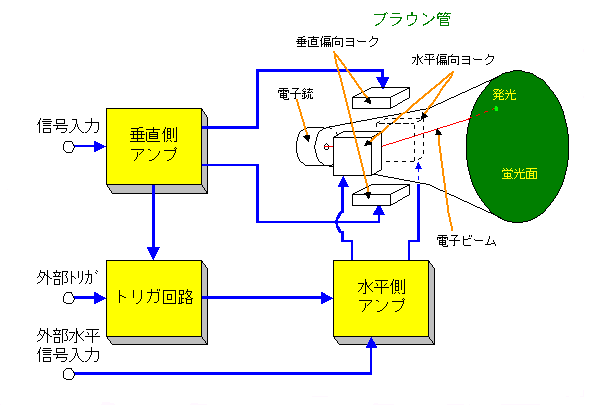
★ ブラウン管の電子銃から、放射された電子ビームは、垂直偏向ヨークと、水平偏向ヨークとによって、所定の方向に曲げられ、蛍光面の所定位置に到着し、そこを光らせます。このビームで、蛍光面に、2 次元の画像を描きます。このため、スキャン (スキャニング )と呼ばれる操作を行います。

★ スキャンは、図に示したように、(a)の2 次元の情報、(1)→(1)→(2)→(2)→(3) ・ ・ 、すなわち、(b) のような、1 次元情報によって描かせることです。
ブラウン管では、同時には、1 点しか表示しませんが、高速で、繰り返しスキャンを行うことによって、画像を表示し続けます。したがって、繰り返し信号の表示に適しています。単発の現象を表示するのには、向きません。
★
オッシロスコープは、アナログの波形を見ることが、目的です。ディジタルオッシロスコープも結局は、ブラウン管上に、アナログの波形を表示させます。
しかし、ディジタルオッシロスコープでは、入力のアナログ信号をA/D 変換器によってディジタル化して、そのディジタル信号を利用します。ブラウン管に表示するためには、ディジタル信号を、D/A 変換器によって、再びアナログ信号に戻します。
したがって、単に入力した波形を、ブラウン管に表示するだけであれば、ディジタルオシロスコープは、何の役にも立ちません。
★ ディジタルオッシロスコープの特徴は、そのディジタル化したデータを、メモリ(記憶装置)に記憶したり、演算処理を行ったりして、その記憶したデータや、演算結果の波形を表示することが、できることにあります。また、パソコンに、測定データを取り込んで、パソコンで、さらに高度なデータ処理を行ったり、することもできます。
ディジタルオッシロスコープでは、単発の現象を、メモリーに記憶させることによって、繰り返し表示させることができます。すなわち、単発の現象の表示が可能です。
★ ディジタルオッシロスコープを、さらに発展させたものが、ロジックアナライザー (ロジアナ )です。
最近は、電子回路の構成要素として、マイクロコンピュータ(マイコン)を使用することが多くなっています。マイクロコンピュータは、バス構成になっており、多数の信号線が並列に走っています。
★ これらの信号は、ほとんどがディジタル信号です。ディジタル信号は、電圧がハイであるかローであるかを識別できれば良く、詳細な電圧値を必要としません。バスなどの、多数のディジタル信号のハイ/ローを、表示できるようにして、マイクロコンピュータなどの信号解析を行うことに特化した、ディジタルオッシロスコープが、ロジックアナライザです。