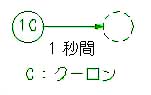
◆ 電流 は、電子の流れです。電流は、単位時間当たりに移動する電荷の量で定義されます(図 2.1-1)。電流の単位は、[A アンペア ]です。
◆ 水を流すのに、水圧 (水の圧力 )が必要であるのと、同様に、電流を流すためには、電圧が必要です(図 2.1-2、図 2.1-3)。ここでも電気を、水に例えています。

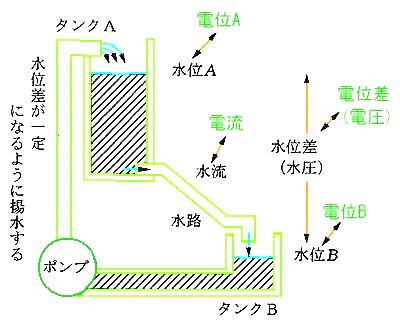
◆ 図 2.1-3 の水圧/水流系に対応する、電気系の具体例が、図 2.1-4 です。この例では、図 2.1-3 の、タンク A 、ポンプ、タンク B の 3 つを合わせたのが、図 2.1-4 の、電池に対応します。
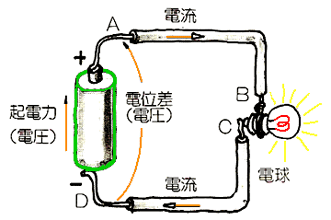
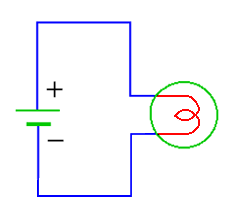
◆ 右側の図は、回路図です。回路図 は、電気の回路を、記号を使って、分かりやすい図にまとめたものです。回路図では、各種の素子を、記号で表しますが、この回路図で使用する記号を、回路図記号 といいます。左側の実態図と対応させれば、この回路図記号の意味は、説明しなくても分かると思います。なお、電池の回路図記号は、細くて長い方がプラス、太くて短い方がマイナスです。
◆
なお、回路図記号は、ここではカラフルに示してありますが、通常はモノクロです。
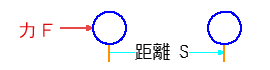
◆ 水位/水流系では、位置のエネルギーを、考えることができます。位置のエネルギーを理解するには、まず、仕事を理解することが必要です。ここで仕事とは、技術用語としての仕事です(図 2.1-5)。仕事 とは、物体に一定の力 F を加えて、力の向きに距離 s だけ動かしたとき、その積 F s のことです(コラム 2.1-1)。仕事の単位は、[J ジュール ] です。
◆
仕事という言葉は、このような技術用語と、一般的な言葉と、2 つの意味を持っています。多くは、文脈から、どちらであるか、分かると思います。とくに、問題になる場合は、断ります。
◆ 質量 m [kg] の物体を、高さ h [m] まで持ち上げたとき、これに要する仕事量 は、mgh です(図 2.1-6)。ただし、ここで g は重力加速度 です。私たち、地上にあるものは、すべて、地球の引力を受けています。もの(この場合は水)を持ち上げるためには、仕事が必要です。
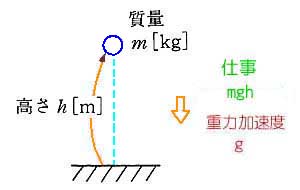
◆ 逆に、持ち上げられた物体は、mgh の仕事をする能力を持つことになります。仕事をする能力のことを、エネルギー と言います。エネルギーには、幾つかの種類があります。ここのエネルギーは、位置(高さ)についてのエネルギーなので、位置のエネルギー と呼んでいます。エネルギーには、位置のエネルギーの他に、運動のエネルギーなどがあります。
★ 仕事という言葉から連想されるものは、何でしょうか。人によって違うと思いますが、「村の鍛冶屋」の唱歌から、鍛冶屋を思い浮かべる人もいると思います。下は、北斎の画く、鍛冶屋です。もっとも、最近では、仕事から、オフィスを連想する人も、多いでしょう。

★ 用語としての仕事や、エネルギーについては、本文では、電圧の定義をするための、最低限の説明しか行っていません。ここでは、もう少し詳しく眺めてみましょう。
仕事 W とは、力 F を加えたときに発生する効果と考えると、分かりやすいと思います。力を加えたときに発生する効果とは、具体的には、動いた、と言うことです。
★ 本文にも示したとおり、力と運動の方向が同じときは、仕事 W は、力 F と移動距離 s との積に等しく、W = F s で、力の単位は、[N、ニュートン] です。
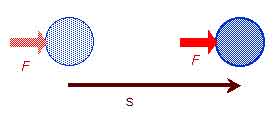
★ しかし、加える力 F の方向と、運動の方向とが異なるときは、力と運動の方向との間の角度を θ とすれば、W = F s cos(θ) となります。
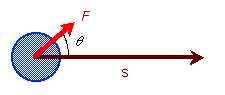
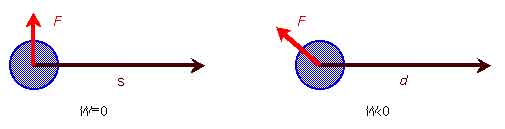
★ いま、θ = 90°とすれば、cos(90°) = 0 ですから、仕事はゼロです(下図左)。すなわち、荷物を押して移動しているとき、横から押しても、何の助けにもならないことを表しています。 また、θ > 90°のときは、cos(θ) < 0 ですから、仕事はマイナスです(下図右)。 これは、荷物を押して移動しているとき、逆から押したら、かえって、邪魔になるということです。
★ また、力に関しては、ニュートンの 3 法則 があります。
★ 第 1 法則(慣性の法則) 力が加わらなければ、運動する物体は、その運動方向に同じ速さで動き続けようとします。これを、慣性 といいます。
★ 第 2 法則(運動方程式) 力 F は質量 m に、加速度 α を掛けたものです。すなわち、F = m α です。
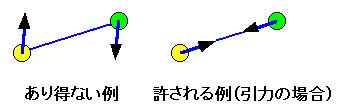
★ 第 3 法則(作用・反作用の法則) 2 つの物体の間に働く力には、一方の物体に作用する力だけでなく、他方への反作用の力があります。作用と反作用の力は、大きさが等しく、方向が逆です。
★ エネルギーは、本文にも示したように、仕事をする能力です。エネルギーには、位置のエネルギー、運動のエネルギー、熱のエネルギー、そして電気のエネルギーなど、いろいろな形のエネルギーがあります。しかし、エネルギーは、形をかえても、その総量は、変化しません。
★ これが、エネルギー保存の法則 です。エネルギー保存の法則が、確立される以前には、多くの永久機関 の発明が試みられました。当然、それらは、成功しませんでした。
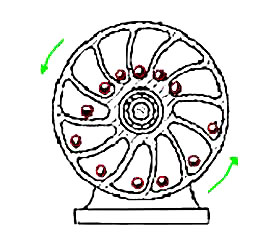
★ 上記も、永久機関の 1 つです。車輪の中に入っている錘の重力で、車輪を回し続けようと言うものです。
★ また、原子核の崩壊のとき、見かけ上は、エネルギーが保存されません。このため、原子核内では、エネルギーは保存されないとする理論も、一時ありました。しかし、当時未知だった、ニュートリノが放出されるのであって、エネルギーは保存されることが分かりました。ニュートリノとは、物質を素通りする粒子で、質量がほとんどゼロの粒子です。
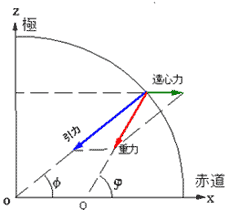
★ 重力という言葉もあります。重力 は、地球が自転していることによって、引き起こされる遠心力と、地球の引力とが合成されたものです。
◆ 電気の場合も水と同様です。ただし、位置(高さ)は、目に見えますし、力は手で感じることができますから、直感性があります。しかし、電気は、目で見ることも、手で感じることもできません。電灯の光は目に見えますが、それは、電気がやった仕事の結果であって、電気そのものではありません。だから、水流に、たとえることが、有効なのです。
◆
さて、話を戻して、電位の高いところに、電荷を移動するには、仕事をしなければなりません。高いところに、水を持ち上げるのと同様です。電位差 (電圧 ) V (ボルト ) は、1 [C、クーロン] の電荷を移動させるのに、1 [ジュール] の仕事を必要とするもの、と定義されます(図 2.1-7)。
◆ 電位 とは、ある電位の基準になるところから測った電圧のことです。したがって、絶対値です。ただし、どこを基準にするかは、必ずしも一定しません。その場所で、基準と考えらるところを、使用します。大地の電位を基準にすることが多く、この場合は、電位の基準となるところを、アース 、グラウンド 、などと呼んでいます(図 2.1-8)。
◆
このお話では、「グラウンド」の言葉を使用します。なお、アース、グラウンドの言葉は、アースする、グラウンドするのように、動詞としても使用します。
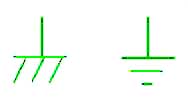
◆
これに対して、電圧は、2 点間の電位の差であり、相対的な値です。
しかし、電位と、電圧の言葉は、しばしば、混同して、使用されています。
◆ グラウンドは、電位の基準となるところですが、その場所は、絶対的なものではありません。あるシステムを考えるとき、その考えているシステムにおいて、基準とみなすことができれば、それで十分です(コラム 2.1-2)。
★ グラウンドといえば、まず思い浮かべるのは、競技のグラウンドでしょう。日本語のグラウンドは競技場ですが、元もとのグラウンドは、要するに地面です。電気の用語としてのグラウンドも、大地からきていますが、電位が安定で、回路動作の基準となる場所は、大地でなくても、全て、グラウンドです。

★ 電気の分野で、グラウンドを使用する目的は、大きく2 つに分かれます。1 つは、本文にもあるように、電気回路の、動作の基準になる場所という役割です。もう 1 つは、保安、すなわち感電による危害の防止です。この保安を目的とするグラウンドは、大地に接続されていなければなりません。また、その仕様は、法的に定められています。
★ このように、グラウンドは、異なった目的に、使用されるので、グラウンド、自体も、2 通りあります。1 つは、大地それ自体を、意味します。もう 1 つは、大地に接続されていないグラウンドで、電気回路の動作の基準として使用するグラウンドです。
ここでは、前者の、回路が動作する基準とな電位としての、グラウンドについて、考えてみましょう。電位の基準になるところといっても、絶対的なものではありません。
★ 高さに例えます。海抜は、高さの絶対的な基準です。しかし、建物の高さを考えるとき、通常は、海抜を意識することはありません。その建物が建っているところの地面を基準にします。
★ 建物 (1) の高さは、B を基準として計り、(A - B) です。建物 (2) の高さは、D を基準として計り、その高さは、(C - D) です。しかし、建物 (1) と建物 (2) とを比較するときは、(D - B) で、考えなければなりません。
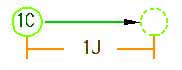
★ 電気の場合も、同様です。機器 (1) と機器 (2) が、各々独立に動作しているなら、そのグラウンドン電位 Vg1 と Vg2 とが異なっていても、問題無く動作します。しかし、機器 (1) と機器 (2) とが、信号線で繋がっていて、信号のやり取りをしているときは、Vg1 と Vg2 とは、電位が、等しくなければなりません。
★ 電気回路の動作の基準となる、グラウンドは、大地に接続されている必要は、ありません。たとえば、航空機に搭載した電気機器は、大地に接続することは、不可能です。また、携帯機器も、大地に接続して使用することは、困難です。しかし、基準となるところの電位が、ふらふらしていたのでは、困ります。

★ したがって、その場所において、最も電位が安定していると、考えれるところを、グラウンドにします。航空機の場合に、最も電位が安定していると、考えられる場所は、機体です。また、機体は、金属でできていますから、機体の電位は、一様です。機体の、どこにグラウンドを取っても、その電位は、等しいと、考えられます。航空機のグラウンドは、機体です。
★ 要するに、その場所で、得られる、最も大ききな、電気の導体が、最も電位が、安定しているわけです。その場で得られる、最も大きな石が、最も安定しているのと、同じことです。大地は、得られる、最大の電気の導体です。
★ グラウンドには、さらに、もう 1 つの役割が、あります。それは、信号の、共通の戻り線 である、と言うことです。
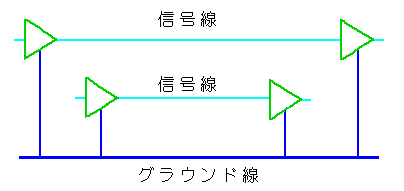
[注] アース、グラウンドという言葉は、いろいろな意味で使われています。これについての詳細は、ノイズ対策講座、第 9 章を参照してください。
★ 単位のお話が、いろいろ出てきました。まず、ちょっと変わった単位を、一つ紹介しましょう。痛みを表す単位、HANAGE です。世界知覚認識学会で、痛みを表す単位として、承認されたものです。
本来、痛みは、個人差が大きく、同じ刺激でも主観によって感じ方が異なります。このため、客観的に数値で表すことは、不可能であると思われていました。
★ しかし、北海道大学医学部の斉藤教授は、「鼻の粘膜は、人体の中で一番個人差が小さい。」ということに注目して、研究を進めた結果、1 cm の鼻毛を、1 N (ニュートン)の力で、引っ張る時に生じる痛みを、1 HANAGE と定義できることを発見しました。
そして、それが、上記学会で、痛みの単位として承認された訳です。なお、下図は、鼻毛カッターです。


★ たとえば、足の小指を、角にぶつけたときの痛みは、2〜3 k HNAGE(キロハナゲ)、お産のときの痛みは、2.5〜3.2 M HANAGE(メガハナゲ)になるのだそうです。
[注] 上記の お話しは フィクションです。
★ さて、ここで、単位 について、解説しておきましょう。
現在私たちが使っている単位系は、国際単位 (SI 単位 )と呼ばれている、国際的に統一された単位系です。この国際単位に基づいて、JIS が決まっています。この「お話」で使っている単位も、JIS に従っています。
★ 昔は、国により、時によって、いろいろな単位が使われていました。日本でも、昔は、尺貫法(長さの単位が尺(約30cm)、目方の単位が貫(3.75kg))が使われていました。現在では、アメリカなど、ごく小数の国を除いて、国際的に統一された単位が使われています。これを SI 単位といいます。
★ アメリカも、既に百年以上前に、SI 単位の元になるメートル条約に調印しています。しかし、国内での準備不足を理由に未だにヤードポンド法を使用しています。
★ SI 単位の構成(したがって JIS 単位でもある)を示します。
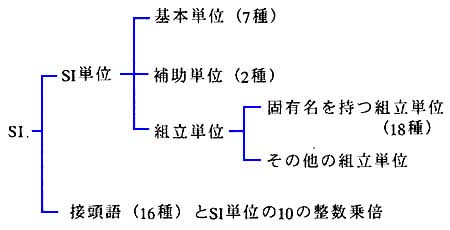
★ 基本単位 と補助単位 は、次の通りです。電気に関しては、「電流」が基本単位になっています。
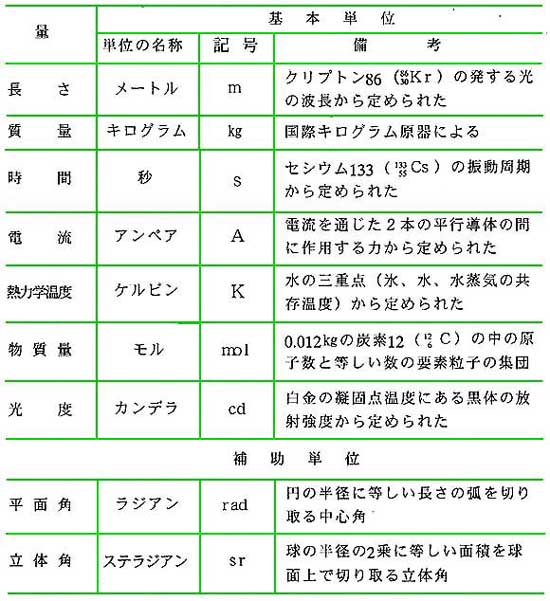
★ 組立単位 は、基本単位と補助単位から誘導される単位です。

★ 接頭語 は、10 の累乗を表します。

★ たとえば、kV : キロボルト 103 V、 mA : ミリアンペア 10-3 A、です。
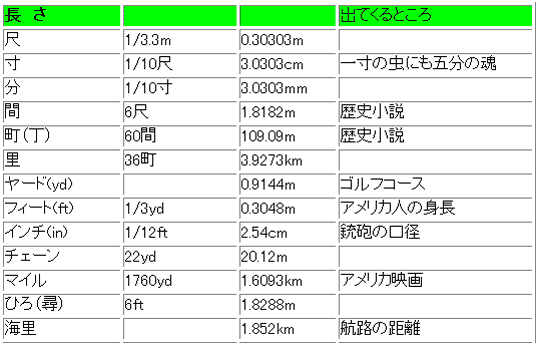
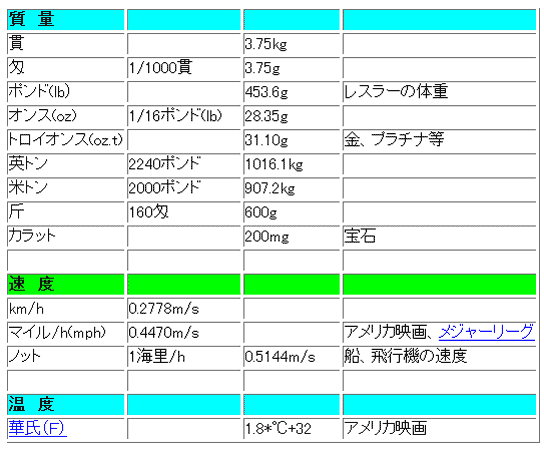
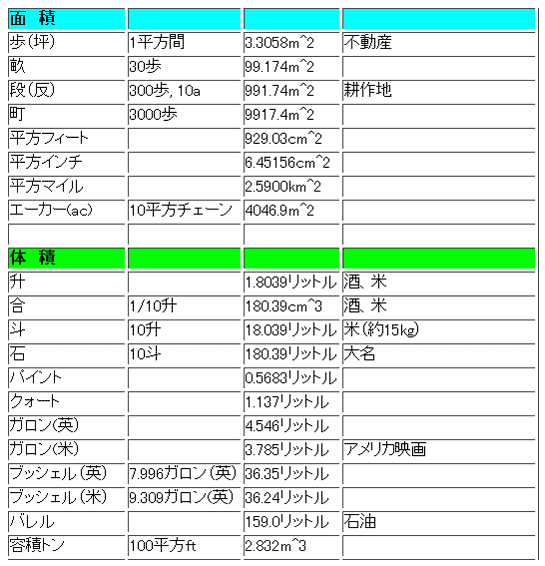
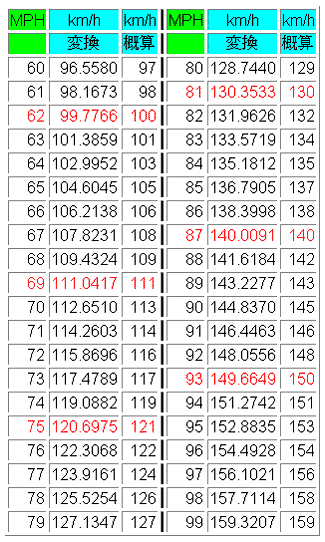
★ 日本では、計量法 によって、SI 単位を使うことが、義務付けられていますが、古い慣用単位も、顔をだすことがあります。また、アメリカが、いまだにヤードポンド法を使っている関係から、ヤードポンド法の単位も多く見受けます。次に、これらの、慣用単位を示します(図中の * は掛け算、^ は累乗です)。