

◆ 直流では、電流と電圧の間には、オームの法則が成立します。実効値を使用すれば、オームの法則は、そのまま、交流にも適用できます。しかし、交流には位相があります。実効値を使用したのでは、位相を考えることができません。位相を考えに入れた、オームの法則の拡張が必要です。
位相を含んで考えるということは、リアクタンスを考え、ベクトルで表す、ということです(図 3.1-1)。図で、C および L に jω が掛かるのは、微分の性質によります(コラム 2.2-5)。
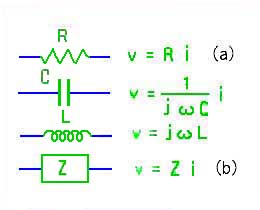
◆ 抵抗 R では、抵抗に掛かる電圧を v、抵抗を流れる電流を i とすれば、オームの法則が成立します(図の(a)式)。リアクタンスを Z とすれば、リアクタンスも、オームの法則と同じ形で表すことができます(図の(b)式)。この形で示した、リアクタンス Z のことを、インピーダンス といいます。インピーダンスは、直流における抵抗の概念を交流に拡張したものです。図に示したような、単体のキャパシタンス C や単体のインダクタンス L だけでなく、抵抗 R をも含めた、複雑な回路も、図の(b)式の Z の形で表すことができるものは、全てインピーダンスです。
インピーダンスは、抵抗の概念の拡張ですから、抵抗単体も、インピーダンスに含まれます。インピーダンスの単位は、抵抗と同じで、[Ω オーム] です。
◆ インピーダンスは、以上のように、ベクトルから定義されますが、別の方法でも、導くことができます。以下、それを示します。
◆ 交流は、ベクトルの形で表すことができます(2.2.(2-B))。ベクトルの形で表すことによって、交流は、分かりやすく表現できます。しかし、ベクトルは、交流だけしか表すことができません。
世の中には、交流以外の波形も沢山あります。たとえば、コンデンサに電池をつないで充電するときの波形は、図 3.1-2 のようになります。
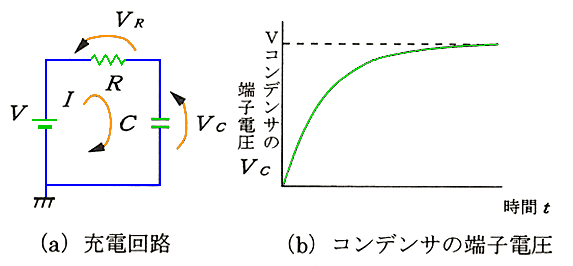
◆ スイッチ SW を閉じた時間が、t = 0 です。充電を開始したときは、コンデンサの端子電圧 vc はゼロであるとします。充電によって、端子電圧 vc が上昇すると、電源電圧との差 vr = v - vc が小さくなりますから、オームの法則によって、充電電流 i が減少します。したがって、端子電圧 vc の上昇速度が鈍ります。端子電圧 vc が電源電圧 v と等しくなれば、充電電流 i はゼロになり、充電は終了します。
このような波形を便利に取り扱う手法に、伝達関数と呼ばれるものがあります。伝達関数のお話から、始めましょう。そしてさらに、伝達関数の基礎になっているのが、ラプラス変換と言うものです。
◆ ここから先、しばらくは、数式の話が出てきます。数式の部分は、いやなら、読み飛ばしても、差し支えありません。ただし、導かれた結果は、利用しましょう。数学屋は、自分で証明できないと、使う気になりません。しかし、技術屋は、証明不可能な法則を利用しています。まして、他の人が証明してくれた事実なら、それを信用して使用することができます。
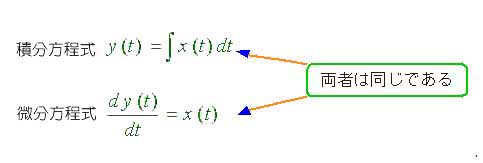
この「お話」では、数式に関しては、必ずしも、厳密な使い方をしていません。たとえば、このお話では、図 3.1-3 が、成り立つものとして、話を進めています。しかし、図の積分方程式と、微分方程式は、数学的には、同じものでは、ありません。
この「お話」では、電気、電子については、できるだけ正確な表現を心掛けています。しかし、背景となる数学については、分かり易さの方を重視して、厳密さは、割愛しています。
◆ さて、ラプラス変換の、お話に入ります。ラプラス変換 は、
_ 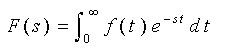
で定義されます。ここで、f(t) は、任意の時間関数です。時間関数 f(t) は、ラプラス変換することによって、s という変数の関数 F(s) に変換されます。この変数 s のことを、ラプラス変換子 といいます。
◆ ラプラス変換することによって、ラプラス変換そのものが、持っている性質から、
微分 d/dt → s
積分 ∫dt → 1/s
と変換されます。そして、ラプラス変換によって変換された変数 s は、四則演算で演算することができます。すなわち、ラプラス変換することによって、微分方程式や、積分方程式は、四則演算に変換されます。
◆ たとえば、
![]()
をラプラス変換すると、
Y = s X + X
です。この式は、四則演算で変形できます。すなわち、
Y = s X + X = (s + 1) X
となります。
◆ 微分方程式や積分方程式を、まともに解かないで、微分記号や積分記号を、単なる変数と同様にみなして、形式的に、四則演算のやり方によって変形すると、結果的に、微分方程式や積分方程式を解くことができるという事実は、始め、経験的に発見され、演算子法 の名で利用されていました。後に、ラプラス変換によって、このことが、数学的に証明されたのです。
ですから、演算子法に立ちかえれば、ラプラス変換を知らないでも、単に「微分記号を s に、積分記号を 1/s に置き換えて、四則演算によって変形することができる」ということだけを、利用すれば良いのです。
◆ ラプラス変換する前の、時間関数 f(t) で表される世界、すなわち、私たちが住んでいる世界を時間領域 、ラプラス変換子 s で表される関数 F(s) で表される世界をラプラス変換領域 と呼びます(図 3.1-4)。
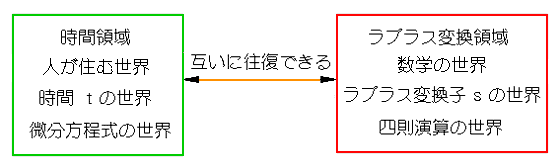
◆ 図 3.1-4 から分かるように、ラプラス変換を利用すれば、微分方程式は、四則演算を使って、簡単に解くことができます。しかし、ラプラス変換の効用は、微分方程式を、簡単解くことが、できるということだけでは、ありません。
もっと簡単で便利な手法を、提供してくれます。すなわち、微分方程式で表される現象を、微分方程式を解くこと無しに、ラプラス変換領域のままで表して、便利に使用することができます。
◆ これが伝達関数 という、手法です(図 3.1-5)。図で、時間関数 x(t)、y(t) のラプラス変換が、それぞれ、X(s) と Y(s) です。伝達関数は、入力に、伝達関数を掛けると、出力になるという便利な性質を持っています。これは、ラプラス変換によって、微分方程式が、四則演算に変換されるからです。時間領域では、入力から、その出力を求めることは、容易ではありません。伝達関数を使用すれば、単に掛け算を行うだけです。
◆ 図にも示されているように、ラプラス変換領域の関数は、X(s) のように大文字を使用し、時間領域の関数は、x(t) のように小文字を使用する習慣があります。このお話でも、この習慣に従うことにします。
これに従うと、X(s) を単に X、x(t) を単に x と、省略して表記することが、できます。ただし、このお話では、はっきり分かるように、X(s)、x(t) のように、省略しないで書きます。
◆ 伝達関数を使用することによって、電気回路の表現や変形が、簡単で、楽になります。
簡単な例として、コンデンサの伝達関数を求めて見ましょう(図 3.1-6)。
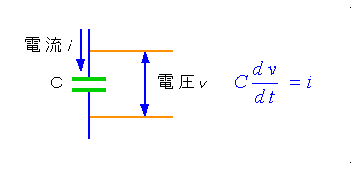
◆ 図の微分微分方程式、すなわち時間領域の式を、ラプラス変換領域で表して見ましょう。d/dt→s と置けば、C s V = I となります。さらに、変形すれば、
_ ![]()
が得られます。この 1/Cs が、コンデンサに流れる電流 I を入力とし、コンデンサの両端に発生する電圧 V を出力とする、伝達関数です。
これを、オームの法則と比べてみましょう。オームの法則は、
v = R i
ですから、抵抗 R と、コンデンサの伝達関数 1/Cs とを置き換えただけです。
[注] オームの法則には、微分/積分を含んでいませんから、ラプラス変換しても、v が V に、i が I になるだけです。
◆ このことは、オームの法則が、抵抗だけでなく、リアクタンス(この例ではキャパシタンス)に拡張して成立することを意味しています。この例は、単純なリアクタンスの例ですが、伝達関数で表現されるものであれば、それが複雑な回路であっても、成立します。回路の伝達関数を F(s) とすれば、
V = F(s) I
となります。
◆ 伝達関数を使用すれば、電圧や電流の波形は、交流に限定されません。たとえば、図 3.1-2 に示したような、任意の関数(波形)であっても、差し支えありません。
というのは、伝達関数の元になっている、ラプラス変換の式における、f(t) が、任意関数だからです。
任意波形で良いのですから、もちろん交流も含みます。波形を交流に限定することによって、後に述べるように、伝達関数から、インピーダンスの概念を導くことができます。逆に言えは、インピーダンスを、さらに、拡張して、一般化したものが、伝達関数です。
◆ 回路を、伝達関数で表現すれば、便利ですが、最終的に欲しいのは回路の波形です。回路の波形を求めるためには、元の時間関数を求める必要があります。これは、ラプラス逆変換 という変換を行うことによって、求めることができます。
しかし、実際には、一々ラプラス逆変換を計算しないで、簡単に回路の波形を知ることができます。というのは、電気回路のほとんどが、定形的なものなので、予め求めてある解を、当てはめれば良いからです。
これも、伝達関数を利用する利点の 1 つです。
◆ 複雑な回路、すなわち、システムは、多数の、簡単な伝達関数の集まりで、表すことができます。このような場合は、システムを図の形で表現すると分かりやすくなります。伝達関数を図の形で表したものを、ブロック図 (ブロックダイヤグラム )といいます。
[注] ブロック図は、図の形式の名称です。ブロック図の形式は、伝達関数以外にも用いられます。
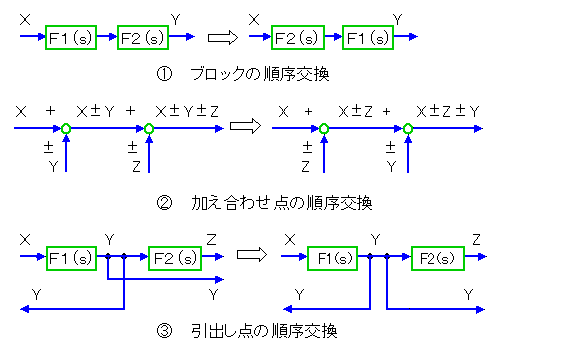
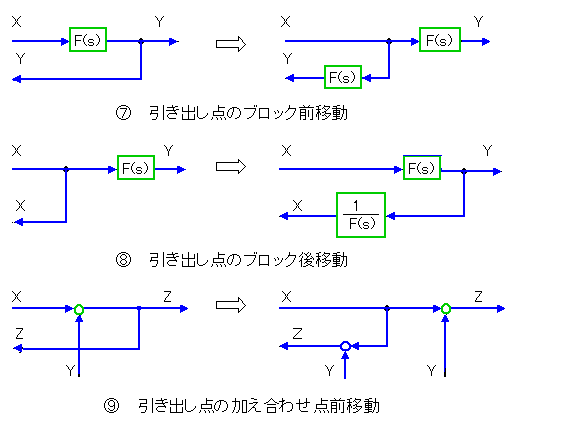
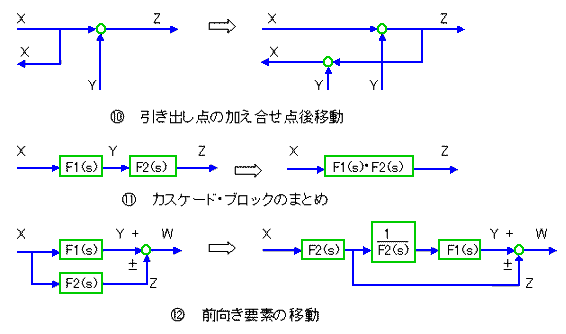
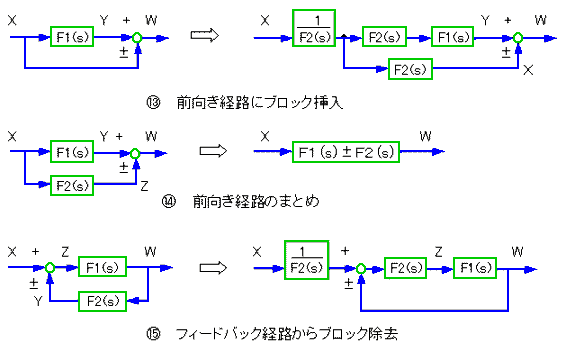
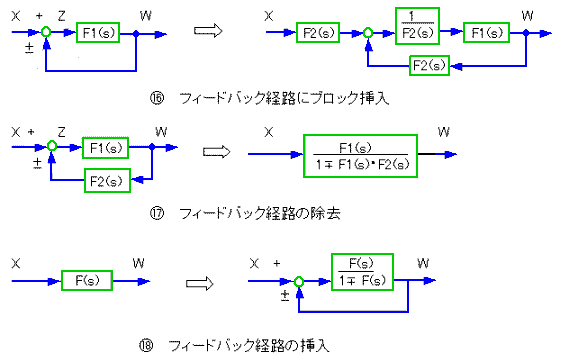
図 3.1-5 は、既に、ブロック図の形で書かれています。図は、1つのブロックですが、複数のブロックを線でつないで、システムを、表します。伝達関数は、四則演算ですから、四則演算の定理にしたがって、変形することができます。この変形法則を、ブロック図の形で表現したものを、ブロック図の変形法則 と呼んでいます。ブロック図の変形法則は、ボリュームがありますから、コラム 3.1-1 に示すます。
★ ブロック図の変形法則を、示します。

★ 伝達とは、伝えることです。伝達関数は、ラプラス変換領域において、入力から、出力に信号を伝えるということです。
単に伝達というと、何でも伝えることになります。したがって、通常は、XX伝達と、伝達の対象を示します。
世間では、何を伝達することに関心が多いかを、インターネットの検索(google 日本語)で、キーワードを「伝達」にして、検索してみました。
上位にあったのは、「免疫シグナル伝達」、「意思伝達」、「触覚伝達」など、人間に関するものが大部分でした。技術的なものでは、「熱伝達」、「動力伝達」、「基板ノイズ高周波伝達」、が、上位に入っています。
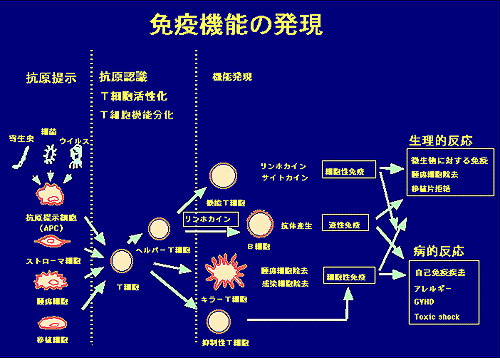
免疫シグナル伝達とは、下記のものです。
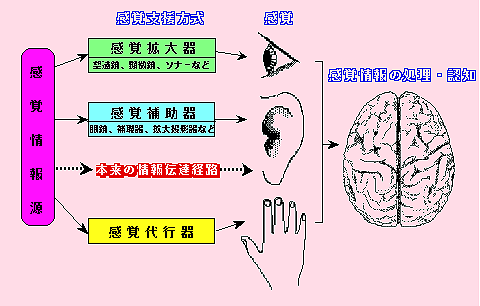
★ 触覚伝達は、人間の感覚伝達において、次のように位置付けられます。
★ 熱伝達は、通常熱伝導 と呼ばれています。ここでは、金属の熱伝導を、考えてみましょう。金属は、電気の導体であると同時に、熱の導体でもあります。
金属の熱伝導を考えるのに先だって、一般の固体を考えます。
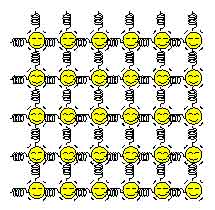
★ 黄色の丸が分子です。分子は、互いにバネで繋がったように、なっています。そして、分子は振動しています。この振動が、熱であり、振動が大きいときが、温度が高いときです。今、この一端を加熱します。暖められたところは、振動が激しくなります。すなわち温度が上がります。この大きくなった振動が、次々と伝わって行くのが、熱伝導です。

★ 気体や液体では、どうでしょうか? 気体の分子は、互いに衝突し合いながら、自由に動き回っています。これを、熱運動 といいます。熱運動は、温度が高くなるほど、激しくなります。この熱運動が、すなわち熱伝導になります。
★ さて、金属ではどうでしょうか? 金属には、自由電子があります。自由電子の運動は、気体中の分子の運動と同様です。自由電子自体の振動が、熱であり、自由電子の移動が熱伝導です。この自由電子が運ぶ熱が、金属中の熱の移動の、ほとんどを占めます。
すなわち、金属は、電気の導体であると同時に、熱の導体でもあります。
★ 電気の伝導に、(電気)抵抗が、あるように、熱の伝導には、熱抵抗 があります。
電流を熱(=電力)に、電圧を温度、抵抗を熱抵抗に、置き換えれば、電気と同様な計算を行うことが、できます。すなわち、
電位差 = 抵抗 × 電流
↓ ↓ ↓
温度差 = 熱抵抗 × 熱(電力)
熱抵抗 = 温度差 / 熱(電力)
となります。
★ このことから、熱抵抗の単位は ℃/W です。