

◆ コンデンサ (キャパシタ )は、リアクタンスの 1 つで、キャパシタンスを利用することを目的に、作られた素子です(図 2.2-22)。
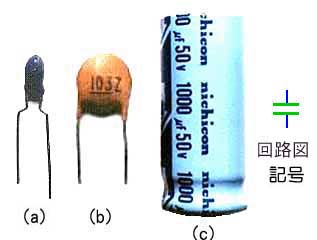
◆ コンデンサの模型的構造は、2 枚の電極 (導体)を、間に絶縁物をはさんで、平行して並べたものです。したがって、その回路図記号も、図 2.2-22 の「記号」に示す形になっています。
コンデンサを、図 2.2-23 のように、つないで、その一方の電極に帯電させると、静電誘導によって、他方の電極にも、これと等しい量の電荷が帯電します。
◆ 電極の電荷を Q [C クーロン]、電極間の電圧を V [V ボルト] とすると、
C = Q / V [F ファラッド ]
の関係があります。この 定数 C のことを、コンデンサのキャパシタンス (静電容量 )といいます。
平行な平板のキャパシタンスは、電極間の距離を d、その面積を S とすれば、
C = ε S / d
・ ・ ・ ・ (2.2-1)
となります。ここで、ε は、電極間の絶縁物の誘電率です。誘電率 は、物質によって決まる定数で、真空(≒空気中)の誘電率 ε は、ε = 1 で、一般には、ε > 1 です。先に示した、クーロンの法則は、真空中のものです。周囲の物質が真空以外のときは、クーロンの法則自体が、式の右辺を周囲物質の誘電率で割った式になります。すなわち、
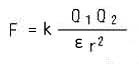
です。なお、ここに示した誘電率は、真空を 1 とした相対値なので、比誘電率 とも呼ばれています。上記の式の定数 k は、真空の誘電率を含んだ値です。
◆ 誘電率の式(2.2-1)から、次のことが分かります。
(a) 面積 S に比例して、キャパシタンスが大きくなります。面積 S を大きくするために、巻き込む構造が、多く使用されています(図 2.1-24)。
[図 2.2-24] コンデンサ構造の一例(フィルムコンデンサ)
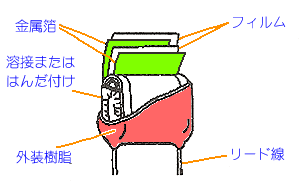
◆ (b) 誘電率 ε が高い物質ほど、同じ面積 S の電極で、大きなキャパシタンス C が得られます。コンデンサの材質は、誘電率が高いものが有利です。コンデンサに使用される、高誘電率材料 を、図 2.2-25 に示します。対照として、誘電率が低い、ポリエチレン なども記載してあります。

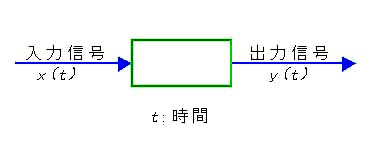
◆ ただし、後に述べるように、キャパシタンスが並列に入っていると、キャパシタンスが大きいほど、遅れが大きくなります(図 2.2-26)。遅れ とは、図に示すように、入力 信号に対して、出力 信号が、時間的に、ずれる現象です。
高速の信号に使用するプリント配線基板は、信号の遅れが小さいことが要求されます。このような場合には、誘電率 ε が低い材質が、望まれます。ケーブル(電線)の絶縁体には、一般に安価なビニールが多く使用されています。しかし、ビニールは誘電率が高く、損失が大きいのです。損失が少ないことが要求されるケーブルでは、絶縁に、低誘電率のポリエチレンが、使用されます。
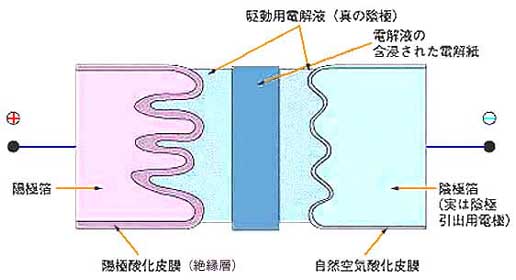
◆ (c) 電極間の距離 d は、短い方が、キャパシタンス C が大きくなります。電極間距離を短くするために、電解質を利用したものが、電解コンデンサ です(図 2.2-27)。電解コンデンサでは、図に示すように、陽極箔と電解液との間に薄い陽極酸化皮膜ができ、この陽極酸化皮膜が、絶縁層になります。この絶縁層は、非常に薄くすることができますから、小さな寸法で、大きなキャパシタンスが得られます。
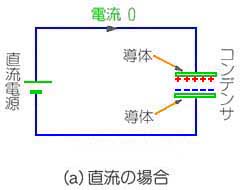
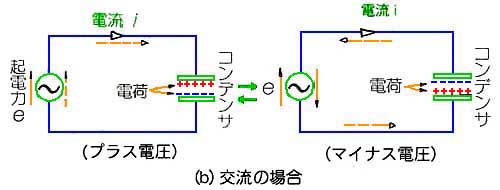
◆ コンデンサに電圧を掛けると、コンデンサを充電 します。直流の場合は、充電すればそれで終わりです。交流のときは、電圧の方向が変わりますから、充放電を繰り返します。すなわち、電流が流れ続けます(図 2.2-28)。
◆ さらに定量的に、調べましょう。コンデンサのキャパシタンス C は、C = Q / V です。電荷 Q を電流に直すと、電流 i は、i = dQ / dt (t : 時間) ですから、
_ 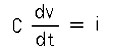
になります。微分は、ベクトルで表すと、位相の 90°の進みです(コラム 2.2-5 参照)。すなわち、コンデンサでは、電流 i は、電圧 v に対して、位相が 90°進んでいます(図 2.2-29)。動画を示します(戻るときは、ブラウザの「戻る」を使用)。
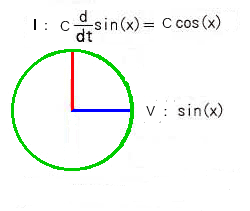
★ コンデンサの名前で呼ばれているものは、電気のコンデンサだけでは、ありません。
まず、プラントなどで用いられるコンデンサ があります。凝縮器 とも呼ばれているものです。コンデンサは、蒸気 を冷やして、液体の水にする装置です。
図は、コンデンサの逆である、蒸発器 と組になっています。蒸発器で発生させた蒸気で、タービンを回します。タービンを回した後の排蒸気を、コンデンサで凝縮 させ、凝縮した水を、蒸発器に落とし、循環させます。

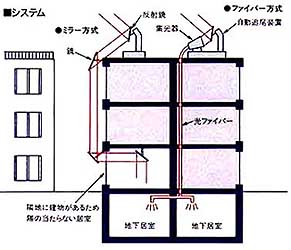
★ また、別のコンデンサもあります。光学における、集光器 です。この例では、屋上の光をコンデンサで集めて、地下の居室の照明に使っています。

★ このように、分野が異なると、同じ言葉が、別のものに使われます。逆に、分野が異なるために、同じものに、別の言葉を使う例もあります。たとえば、電気や機械の分野で、周波数特性と呼んでいるものは、自動制御の分野では、言葉は似ていますが、周波数応答の言葉を使っています。
★ さて、電気のコンデンサに関する話題を1つ紹介します。大容量のコンデンサは、電池の代わりとして使用することができます。電池には、1 次電池と、2 次電池とがあります。1 度しか使えない使い捨ての電池が 1 次電池 で、充電して反復使用できるのが 2 次電池 です。この 2 次電池の代わりに、コンデンサを使おうというものです。
この目的に、使用できるのが、電気 2 重層コンデンサです。
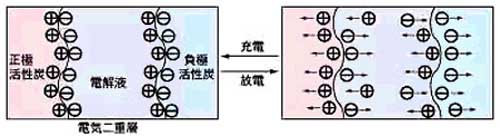
★ 電気 2 重層コンデンサ は、電解コンデンサの一種ですが、普通の電解コンデンサと比べて、エネルギー密度が非常に高いことが特徴です。
エネルギー密度 は、電池性能の指標の1つで、電池の重量または体積当たりに蓄える電気量です。重量当たりのエネルギー密度が高ければ、同じ容量で、軽い電池が作れます。体積当たりのエネルギー密度が高ければ、同じ容量で、小さい電池を作ることができます。
両方ともに優れていれば理想的ですが、実際は、どちらを重視するかで、電池の選択が異なります。
★ 最近、電気 2 重層コンデンサのエネルギー密度が、2 次電池並に高いものが、開発されています。これが実用化すれば、ノートパソコンや携帯電話などの使い勝手が、大幅に向上します。電気自動車への応用も考えられます。
★ 地図には、ラスターデータ とベクトルデータ との、2 つの表現形式があります。ラスターデータというのは、地図を、普通の図面の形で表したものです。すなわち、図形を、2 次元の画素で表現します(図 1、図 3)。これに対して、ベクトルデータは、図形を、多数のベクトルの形で表し、座標でベクトルの位置を示します(図 2、図 4)。
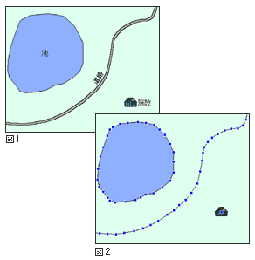
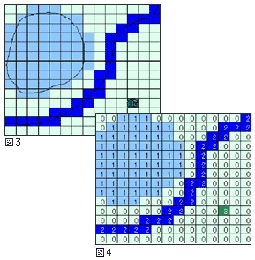
★ 地図情報を、コンピュータに収容し、コンピュータで地図を画かせる場合は、ベクターデータが、優れています。コンピュータのメモリ容量が、大幅に少なくて済み、かつ縮尺を自由に変更できるからです。
★ さて、本題に入り、ベクトルの微分と積分について、示します。
まず。正弦関数については、sin(x) を微分 すると、cos(x) になります。
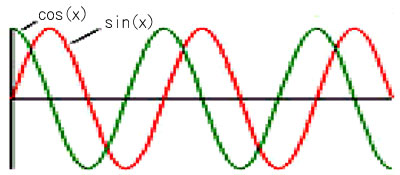
★ 図から、cos(x) は、sin(x) よりも、位相が 90°進んでいることが分かります。sin(x) を積分 すると、-cos(x) ですから、逆に、位相は 90°遅れます。
これをベクトルで表すと、
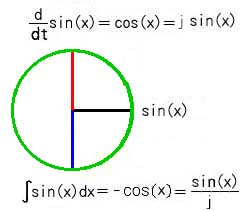
となります。ベクトルに j を掛けることは、90°位相を進ませ、j で割ることは、位相を 90°遅らせることを意味します(コラム 2.2-2複素数の基本性質)。
なお、この図も、位相の関係だけを、示す図です。
★ 次に、大きさを考えてみましょう。
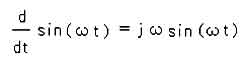
です。微分することは、90°の回転と共に、振幅を ω倍することを意味します。