

◆ インピーダンスは、単体のリアクタンスだけでは、ありません。リアクタンスや抵抗を組み合わせることによって、より複雑な特性のインピーダンスを作ることができます。
ある回路を通過させることによって、その入力と出力との周波数特性を変化させる回路を、フィルタ と呼んでいます。フィルタは、その特性によって、大きく 4 つに分類することができます(図 3.2-4)。

◆ ローパスフィルタは低域通過フィルタ 、ハイパスフィルタ は高域通過フィルタ 、バンドパスフィルタ は帯域通過フィルタ 、バンドエリミネーションフィルタ は帯域阻止フィルタ とも呼ばれています。
フィルタは、抵抗 R とコイル L との組み合わせと、抵抗 R と コンデンサ C との組み合わせの、どちらを使用しても、同じ特性のものを、作ることができます。通常は、コイルよりも、コンデンサを使用する方が、寸法が小さく、価格も安くできるので、コンデンサを使用することが、多いのです。
◆ 以下は、コンデンサと、抵抗を組み合わせたフィルタについて、解説します。なお、フィルタは、ここに述べるフィルの他に、増幅器と組み合わせた、より優れた特性を持つフィルタがあります。増幅器と組み合わせて作ったフィルタを アクティブフィルタ (能動フィルタ )、ここに述べる、抵抗 R とリアクタンスだけで作ったフィルタを、パッシブフィルタ (受動フィルタ )といいます。
★ 増幅は、文字通り幅を増やすことですが、幅に限らず、増やすことは、何でも増幅と呼んでいるようです。資産の増幅は、こんな嬉しいことはありませんが、コンピュータウィルスの増幅は、困ります。
★ 増幅器 (アンプリファイア 、アンプ )は、読んで字のごとく、振幅を増やす回路です。電気以外の増幅器、たとえば、光増幅器なども、ありますが、ここでは、電気の増幅について説明します。
増幅器は、電源などを内蔵した、独立した機器になっているものと、

★ IC の形で供給され、プリント基板に回路を組んで使用するタイプとがあります。この IC を、オペアンプ といいます。

★ 増幅器は、また、何を増幅 するか(振幅を増やすか)で、電圧増幅器 、電流増幅器 、電力増幅器 の、3 つに分けられます。
★ 特殊な場合を除いて、増幅のためには、外部からパワー(電源)を供給する必要があります。
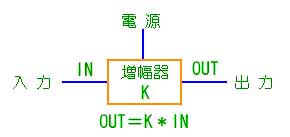
★ 入力 IN と出力 OUT との振幅比を、増幅率 (利得、ゲイン) K といいます。
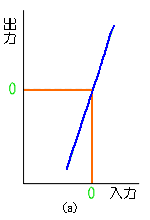
最も普通の増幅器では、プラス/マイナスの電源を供給し、入出力の電圧は、ゼロ(グラウンド)を中心に、プラス/マイナスに振れます(a)。
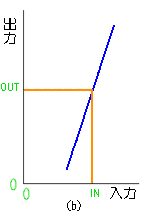
しかし、最近は、プラス単電源で動作する増幅器も多くなっています。この場合には、入出力の電圧は、電源とグラウンドの中点(図の IN、OUT)を基準として動作します(b)。
◆ ローパスフィルタ の基本は、抵抗 R とコンデンサ C とを組み合わせたもので、RC フィルタ と呼ばれています(図 3.2-5)。
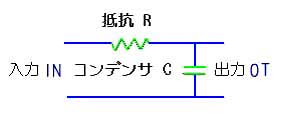
◆ RC フィルタは、図に示されているように、抵抗 R とコンデンサ C との分圧点を取り出したものです。分圧の式(2.1-2)´ は抵抗だけでなく、インピーダンス一般にも成立します。したがって、出力 OT は、入力 IN に対して、
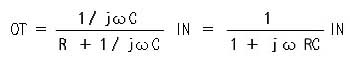
となります。すなわち、RC フィルタのインピーダンスは、1/(1 + jωRC) です。RC フィルタの周波数特性を図 3.2-6 に示します。
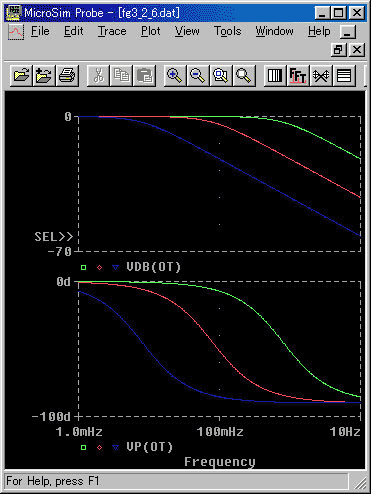
◆ RC フィルタでは、抵抗 R キャパシタンス C との積 RC のことを、時定数 (タイムコンスタント ) T といいます。RC フィルタの周波数特性は、波形に関しては、時定数 T に依存しないで、一定です。しかし、図から分かるように、時定数 T に比例して、周波数方向に、平行移動します。
低い周波数では、振幅比が 0 dB すなわち 1 ですから、減衰無しに、通過します。高い周波数では、減衰があります。低い周波数の信号を、減衰無しに通過させることから、ローパスフィルタの名がつけられたわけです。
★ フィルタとは、ろ過 することです。しかし、何をろ過するかは、様々です。
最初の話題は、光学フィルタ、要するに写真用のカメラに付けるフィルタです。特殊効果を狙ったフィルタもありますが、最も一般的なのは、レンズ保護を兼ねた、UV(紫外線)カット用のフィルタです。

★ 次は、画像のフィルタです。フィルムカメラの写真も、スキャナによって、パソコンに取り込むことができます。しかし、パソコンに取り込むなら、デジカメが便利です。パソコンのソフトウェアで、フィルタ処理(画像処理)を行って、画質を高めたり、各種の効果を出すことができます。
筆者は、ホームページで、この「お話」などのweb 講座の他に、写真集「池畔」を公開しています。この写真は、デジカメで撮ったものです。自動露出で使っています。自動露出だと、被写体によっては、適正な露出が得られません。しかし、露出を気にしないで撮り、露出不足などは、パソコンに取り込んでから、フィルタで救済しています。
★ 次の例は、お遊びです。ブサイクを美人に、美人をブサイクに、フィルタします。画像に、その微分を加えると、はっきりした画像になります。これが美人処理です。逆の処理では、ややボケた画像になります。これがブサイク処理です。

URL(ホームページアドレス) を入れておきます。各自で試みてください。なお、この種の URL の継続性は、保証されません。
★ インターネット関連のフィルタもあります。ウィルス対策ソフトは、コンピュータウィルスに対するフィルタです。迷惑メール(勝手に送っくる迷惑な電子メール)のフィルタもあります。次に示すのは、ホームページ閲覧のフィルタです。このフィルタは、親が、子供が見るページに、フィルタを掛けて、子供に、有害なページを見せないようにします。
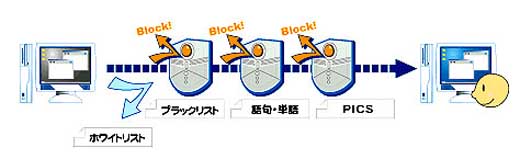
★ これは、まじめな使い方ですが、お遊びもあります。次のフィルタは、ホームページの文章に、フィルタを掛けて、標準語を方言に変えています。
これも、URL を入れておきます。
[コラム 3.2-5] 抵抗 R とキャパシタンス C との積が時間になる
★ 抵抗 R とキャパシタンス C との積を時定数 T といいます。時の文字がつくということは、積 RC が、時間の次元を持っているからです。一見奇妙に思われますが、間違いではありません。
コンデンサは、すでに示したように、充電された電荷を Q、電極間の電圧を V とすれば、C = Q / V です。R は、オームの法則によって、R = V / I ですから、これらを代入すれば、
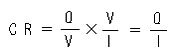
となります。ここで、電流 I は、I = Q / T ですから、
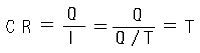
となり、CR = T が成立します。
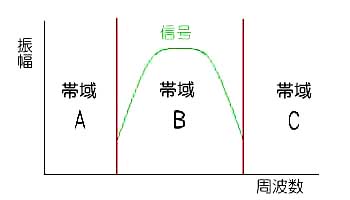
◆ 一般に信号は、ある周波数の範囲に存在します。逆にいうと、実用上信号が存在しない周波数の範囲があります。このような、ある周波数の範囲のことを、周波数帯域 (略して単に帯域 )といいます(図 3.2-7)。図で、A と C は、信号が存在しない周波数帯域、B は、信号が存在する周波数帯域です。
◆ フィルタでは、信号を通過させる周波数帯域を、通過域 、信号を阻止する周波数帯域を、阻止域 といいます(図 3.2-8)。
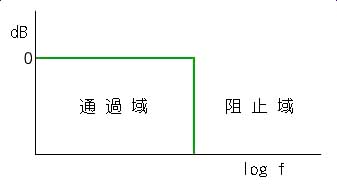
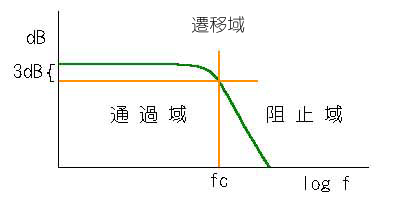
◆ 理想的には、通過域と阻止域とは、図のように完全に分かれて欲しい訳ですが、実際には、図 3.2-6 の RC フィルタの特性からも推定されますが、図 3.2-9 のように、境界が、だれて、しまいます。このようなとき、図に示すように、通過域の、フラットの部分の高さから、-3dB のところの周波数を、通過域と阻止域との境界と定義します。この境界の周波数 fc のことを、カットオフ周波数 (遮断周波数 )といいます。
また、通過域と、阻止域との中間の領域を、遷移域 といいます。
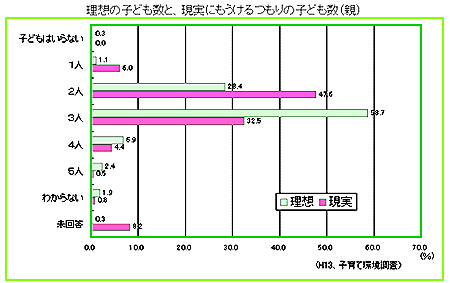
★ 世の中、理想と現実があります。現実が全て理想どおりに行くのが理想ですが、現実には理想どおりには行きません。下図は、産みたい子供の数と、現実に産んだ子供の数を調べたものです。
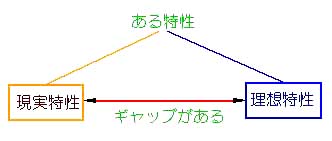
★ 電子の世界においても、各種の特性には、あるべき姿としての理想特性 と、実際には、このようにしかならないという、現実特性 とがあり、その間には、ギャップがあります。
フィルタにおいても、その例外では、ありません。フィルタの通過域と阻止域の境界は、理想的には、図 3.2-8 に示したように、きっぱりと分かれているべきです。しかし、現実には、図 3.2-9 のようにだれてしまいます。
★ また、現実の世界では、必ず誤差 があり、絶対的に正確なものは、数学を除いては存在しません。その誤差に対しては、これだけの大きさの誤差なら許容されるという、許容誤差 が存在します。
★ 誤差が許容誤差の範囲に入っているなら、現実の世界では、正しいと考えて差し支えありません。現実特性が、許容誤差の範囲に入らないときだけ、現実特性と理想特性とを区別して考えます。現実特性が、許容誤差の範囲内に入っているなら、理想特性と現実特性とを区別する必要はありません。
★ 許容誤差の大きさは、時と場合によって異なります。したがって、許容誤差が、厳しいときだけ、理想特性と現実特性とを、区別すれば良いわけです。下図の左側は、現実特性が、許容誤差の範囲内に入っています。現実特性と理想特性とを、区別する必要はありません。
★ 具体例として、コンデンサ C と、コイル L の周波数特性の現実特性を見てみましょう。
★ 図から分かるように、周波数が低い範囲では、誤差はありますが、ほぼ、理想の特性を持っています。しかし、高い周波数では、コンデンサ C はインダクタ L に、インダクタ L はコンデンサ C に化けてしまいます。
★ この、コンデンサがキャパシタンス C であり、コイルがインダクタンス L である、とみなすことができる、周波数帯域が、現実に使用可能な周波数帯域です。この周波数帯域を超えて使用すると、その素子は、役にたちません。
★ この、現実に使用可能な周波数帯域は、コンデンサ C や、インダクタ L の機種によって、大きく異なります。したがって、実際に使用する周波数帯域に合わせて、コンデンサやコイルの機種を、選定する必要があります。コンデンサ C やインダクタ L は、周波数特性だけでなく、いろいろな、特性について、それぞれの機種による特性値の違いがあります。
★ コンデンサやコイルは、目的、用途によって、適切な機種を選定する必要があります。
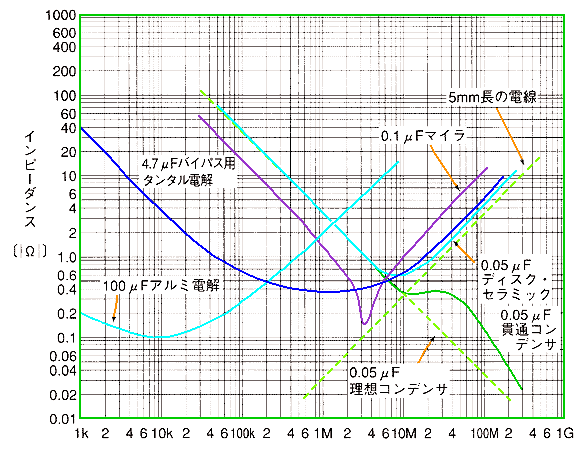
★ この図は、コンデンサの機種による、周波数特性の違いを示したものです。ごく、大雑把に言って、キャパシタンスが大きいものほど、低い周波数でしか使えません。
広い周波数帯域で、使用する必要があるときは、大小 2 つのコンデンサを併用します。
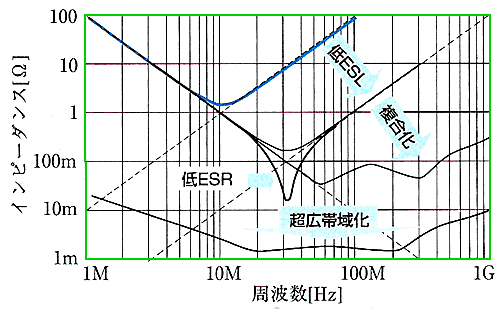
★ 上記は、資料が古いので、最近の製品は、これよりも、周波数特性が改良されています。その傾向を示します。図で、複合化は、大小 2 つのコンデンサを使用したときの特性です。超広帯域化が、最近の製品です。1 個の素子で、従来の素子の複合化よりも、優れた特性を、持っています。
★ なお、回路図上の記号は、各素子は、理想特性を持つものとして、書かれています。コンデンサは、あくまでもコンデンサです。したがって、回路図の上では、現実特性は 、表現されません。このことから、たとえば、コンデンサが有する、現実特性としての、抵抗成分や、インダクタンス分のことを、回路図に無い回路 といいます。