

◆ 回路に、ある波形を入力したときの出力波形のことを、その入力に対する応答 といいます。応答波形を見ることによって、回路の特性(性質)を知ることができます。
この目的に利用する入力波形は、その回路の特性を、できるだけ分かりやすく表すことができる、波形であることが望まれます。この目的に使用する入力波形は、幾つかあります。
その、代表的な、2 種類の応答に、ステップ応答 と、周波数応答 があります。これらの応答によって表現した特性を、それぞれ、過渡特性、周波数特性と呼んでいます(図 3.1-7)。
自動制御の分野では、ステップ応答、周波数応答の言葉が、専ら使われていますが、電気の分野では、過渡特性、周波数特性の方が、多く使用されています。以下、過渡特性、周波数特性の言葉を使用します。
過渡特性は、1 つの波形を示したものですが、周波数特性は、周波数が異なる多数の正弦波形を入力した結果を取りまとめたものです。

◆ 過渡特性 の入力信号波形は、図 2.2-26 に示した入力信号のような、ステップ状の波形です。図 3.1-2 の波形も過渡特性です。過渡特性は、回路の特性が、直感的に、分かりやすく表現されるという、特徴があります。その代わり、大まかなことしか分からないという、欠点があります。
これに対して、周波数特性は、直感性では劣りますが、細かな特性が良く表現できるという、特徴があります。
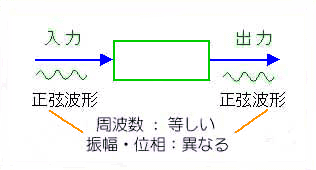
◆ 周波数特性は、回路の入力に正弦波形を加えます。その出力には、はじめ、過渡的な波形が現れますが、やがて定常状態になります。定常状態では、出力波形も正弦波形で、その周波数は入力の周波数と等しくなります(図 3.1-8)。
この正弦波は、入力と出力の周波数は等しいのですが、振幅比と位相差は異なります。そして、入力の周波数を変えると、入力周波数に伴って、その、振幅比と位相差が変化します。
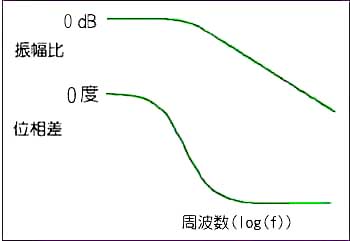
◆ 入力周波数に対する、入出力間の振幅比 (ゲイン 、利得 )と、位相差 (フェイズ )をプロットしたものが、周波数特性 です。図 3.1-2 のコンデンサ充電時の周波数特性は、図 3.1-9 のようになります。
図の横軸は、周波数 f の対数、すなわち、log(f) で、縦軸は、振幅比をdB (デシベル)で、位相差を °(度)で目盛ってあります。この形式の図を、ボード線図 といいます。
周波数特性を、図の形で表現する方法は、他にも幾つかありますが、ボード線図が、最も一般的です。
[図 3.1-9] コンデンサ充電時の周波数特性(ボード線図)
◆ ここで、振幅比のdB (デシベル ) の d は、SI 単位の接頭語の「デシ」で 10-1 を意味します。B は、電力比の対数です。すなわち、2 つの電力を、p1 および p2 とすれば、log(p1 / p2) のことです。比ですから本来無名数のはずですが、電力比は、多く使うので、とくに、B (ベル )という単位名称を付けたものです。
図 3.1-9 は、電力比ではなく、電圧の振幅比です。電力を p、電圧を v、抵抗を R とすれば、
p = v2 / R
の関係があります。電圧比を電力比に換算すると、ベル = 2 × 10デシベル = 20デシベル となります。はじめの 2 は、v2 の 2乗の 2 で、後の 10 は、デシの 10 です。電流比の場合も同様に、ベル = 20デシベル です。
このように、デシベルによる表示は、電圧/電流比のときと、電力比のときとで、異なることに注意してください。
★ 信号といえば、第一に思い浮かべるのは、町角や、鉄道の信号機でしょう。下図左の 2 つは、初期の街頭の信号機です。右は、現在でも使っているらしいですが、旧式の鉄道信号機です。



★ 下図左は、タブレットの受け渡しです。単線区間では、1 つの区間に、1 列車しか入らないように、タブレットを持った列車だけが、その区間の運転を、許可されます。タブレットは、信号機を補助し、安全の向上に役立っています。


★ 最近、信号機のランプは、電球ではなく、LED が多くなっています(上図右)。電球と比べて、省エネ、ランプの長寿命化に役だっていますが、見やすさの点でも、効果があるようです。とくに、直射日光が当っているときに、見やすくなっています。
★ さて、信号は、次のように、定義されます。
(1) 情報を伝達するために記号化、符号化したもの
(2) 情報を送る物、方法、情報を表現したもの
(3) 日常的には、鉄道・道路などに設置され、人や車の通行を規制する信号機の意味でも用いられる
★ 信号の、本来の定義は、上記の、(1)または(2)です。この、お話でも、信号は、この意味で使っています。
★ このお話では、今まで、信号は、正弦波形など、きれいな波形を、扱ってきました。しかし、一般の波形は、もっとランダムな波形です。
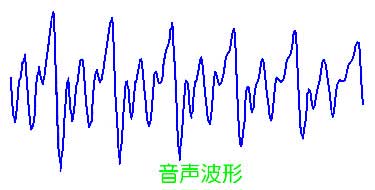
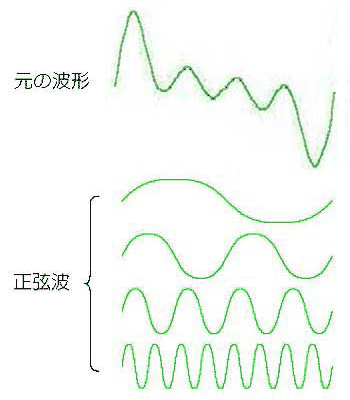
★ これは、音声波形の一部分を切り出したものです。音声ですから、ほぼ、一定の繰り返しです。もっと完全にランダムな波形もあります。しかし、この音声波形も、きれいな正弦波形ではありません。このような信号波形は、多数の、互いに周波数が異なる正弦波形の、集まりとして、表すことができます。たとえば、下図は、元の波形が、4 つの周波数の、信号の集まりです。
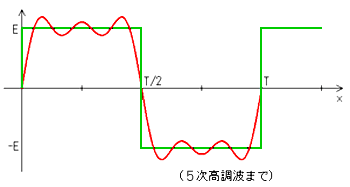
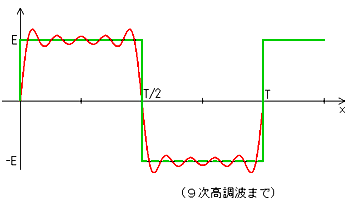
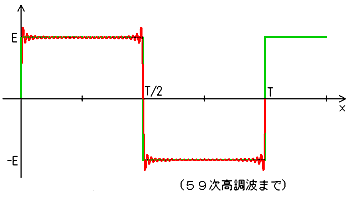
★ 方形波など、角がある信号波形は、理論的には無限大の周波数の信号を含んでいます。
信号に含まれている正弦波形の中で、最も低い周波数のものを、基本波 といい、基本波より高い周波数のものを、高調波 といいます。高調波は、さらに、基本波の n 倍の周波数のものを、第 n 次高調波といいます。
上記の、元の波形は、第 4 次高調波までを含み、各高調波の振幅は、基本波と等しい、波形です。
★ 角がある波形は、かなり高次の高調波まで含めないと、信号の波形が鈍ってしまいます。高調波の次数と波形との関係を示します。
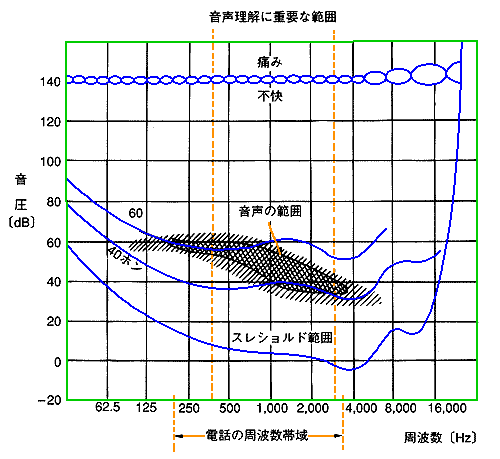
★ 人が、耳で聞くことができる音は、音声よりも、広い周波数帯域があります。
◆ 過渡特性は、時間領域の応答ですが、伝達関数から求めることができます。周波数特性も、伝達関数から簡単に求めることができます。したがって、回路の伝達関数を求めておけば、各種の応答特性を、求めることができます。
ステップ波形(図 2.2-26 の入力信号の波形)のラプラス変換は、1/s です。回路の伝達関数を F(s) とすれば、その過渡特性の出力 Y(s) は、回路の伝達関数に、入力(ラプラス変換形)を掛けたものですから、
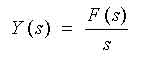
となります。
◆ 周波数特性は、異なった周波数の正弦波形を逐次入力して、求めることができます。しかし、もっと簡単に、伝達関数で、s→jω と置くことによって、直ちに、周波数特性が、求まります。
周波数特性は、フーリエ変換と呼ばれる変換そのものです。フーリエ変換 は、
![]()
です。これは、ラプラス変換の式で、s→jωとしたものです。今まで断りませんでしたが、実はラプラス変換子 s は、複素数です。したがって、jω は、s の実数部をゼロとした特殊なケースです。
すなわち、ラプラス変換は、フーリエ変換を含んでいます。s→jω と置くことには、何も問題はありません。
ところで、e-jωt は、外観は指数関数の形をしていますが、実は三角関数です。すなわち、
e-jωt = cos(ωt) - j sin(ωt)
という関係があります。したがって、フーリエ変換は、
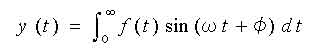
と同じ意味を持っています。積分の中で、関数 f(t) に sin(ωt + φ) を掛けています。これを積分するということは、もし、関数 f(t) が、sin(ωt + φ) と全く関係が無いとすれば、これを積分しても、値はゼロになるでしょう。
関数 f(t) の中に、sin(ωt + φ) の成分を含んでいれば、積分した値は、含まれている sin(ωt + φ) に比例した値を持つと考えることができます。
すなわち、フーリエ変換は、式の上で、関数 f(t) の周波数特性を求めていることになります。フーリエ変換は、周波数特性そのものです。
フーリエ変換は、ラプラス変換において、s→jω と置いたものです。ということは、伝達関数 F(s) において、s→jω と置いた、F(jω) は、周波数特性であるということです。このことから、F(jω) のことを、周波数伝達関数 とも呼んでいます。
◆ 電流を入力とし、電圧を出力とする、コンデンサの、伝達関数は、先に示したとおりです。この伝達関数で、s→iω と置けば、
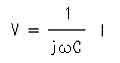
となります。これは、図 3.1-1に示した、インピーダンスそのものです。すなわち、インピーダンスは、電流を入力とし、出力を電圧とする、伝達関数において、s→jω と置いたものです。伝達関数において、s→jω と置いたものは、すなわち、フーリエ変換であり、周波数特性を意味します。インピーダンスは、その要素の、周波数特性を表したものです。
インピーダンスは、交流における特性です。伝達関数は、過渡特性などを含む、一般波形における特性を表します。一般波形には、交流も含みます。すなわち、伝達関数は、インピーダンスを含み、インピーダンスよりも、広い概念です。