◆ フィードバック制御系は、制御要素 の集まりです。ここで制御要素とは、制御対象、コントローラなど制御系を構成する要素のことです。
制御要素は、実際にはものを加工したり、動かしたりしています。しかし、制御の問題を考えるときは、すべて信号の流れ として、抽象化して取り扱います (図 3-1-1)。
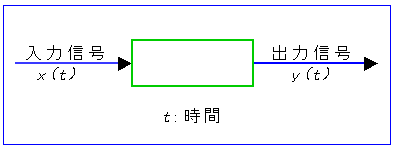
◆ 図に示すように、信号は、ある要素に入力し、要素で処理されて、出力信号となって出力されます。
◆ 制御の問題を考えるときには、この信号は、時間とともに変化する時間関数として、とらえることが必要です。
入力が変化しても、直ちに出力は変化しません。図 3-1-2 に示すように、入力と出力との間には「遅れ 」があります。
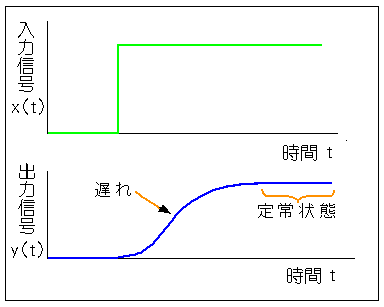
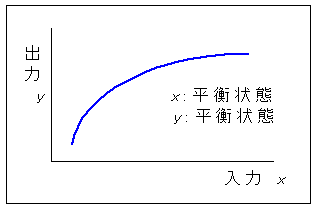
◆ 入力値が一定の状態が続けば、やがて出力も定常状態になり、一定値になります。これを平衡状態 といいます。フィードバック制御では、平衡状態における、入力( x )と出力( y )との関係を「静特性 」と呼んでいます (図 3-1-3)。
◆ 制御以外の分野では、この静特性が問題になります。しかし、フィードバック制御の分野では、静特性も重要ですが、制御成績により大きく影響するという点で、「遅れ」が大きな問題になります。
遅れによって生じる、過渡的な、入力と出力との時間的な関係を、「動特性 」といいます。時間による変化が問題になりますから、変数( x や y )は、時間関数( x(t) や y(t) : t は時間)としてとらえることが必要です。制御系の解析と設計には、この動特性が必要です。
◆ なぜ、このような遅れが発生するのでしょうか。それは、過去の値が、現在の状態に、影響しているからです。過去の値が、現在に影響していると言うことは、数学的には、入力と出力との間に積分の関係があることを意味します。
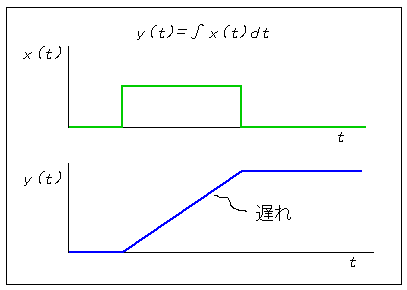
入力と出力との関係が、代数方程式で表わされる場合には、入力の結果は直ちに出力となって現れますから、遅れは存在しません。これに対して積分 は、過去の値を蓄積しますから、遅れとなって現れます (図 3-1-4)。
◆ ところで、積分と微分 とは逆演算の関係にあります。逆演算であるということは、積分を含む方程式は、微分を含む方程式に、変換することができるということです (図 3-1-5)。
以上から、「遅れが存在する系は、微分方程式 で表わされる」ということが言えます。
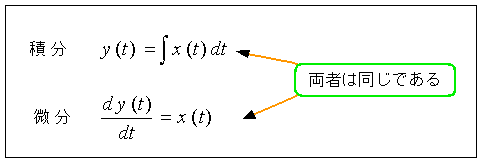
◆ この講座では、数学的な事柄は簡単に結果だけを示します。また、実用上差し支えない範囲で簡略化して(ごまかして)示します。たとえば 図 3-1-5 は数学としては、正確ではありません。
ただし、定性的な説明を、分かりやすくていねいに行います。
◆ 微分方程式と聞いて「ゾッ」とする読者もいるかと思います。しかし、心配する必要はありません。この講座では、数学的なことは、易しいお話として取り扱います。
微分方程式を、まともに解いたりすることはありません。制御の問題では、微分方程式を、まともに取り扱う代わりに、ラプラス変換と呼ばれている手法を利用します。
ラプラス変換 そのもは、難しい数学ですが、その結果を利用するのは、実に簡単なことです。
◆ 微分は d/dt で表わします。すなわち d/dt は微分記号ですが、この微分記号を"s"という変数に置き換えます。
d / dt → s
s は単なる変数ですから、加減乗除の演算で式を変形することができます。
ラプラス変換とは、結論だけいえば、たったこれだけのことです。
しかしこの結果は、極めて有用です。微分方程式を、まともに解かないで、四則演算として変形することによって、微分方程式を解いてしまうことができるのです。
フィードバック制御では、ラプラス変換を利用して、制御系の解析や設計を簡単に行うことができます。ラプラス変換を利用して微分方程式を解く必要もありません。もっと、簡単です。
◆ ラプラス変換とは、数学的には、式(3-1-1)に示す変換を行うことです。この式のところは、いやなら、読み飛ばしてください。
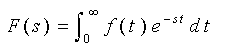・・・(3-1-1)
ここで f(t) は、時間 t の関数で、ラプラス変換の対象となる関数です。このラプラス変換式を計算すると(変換を実行すると)、時間 t が消え、代わりに変換式中の s が残ります。
すなわち、時間関数 f(t)が s の関数 F(s) に変換されます。この変換が、ラプラス変換です。変数 s のことを、ラプラス変換子 といいます。
ラプラス変換を実行すると、関数 f(t) に含まれていた微分と積分は、
d/dt → s
∫dt → 1/s
のように変換されます。すなわち、微分と積分は、ラプラス変換子に置き換えられます。
また、式は示しませんが、関数 F(s) を関数 f(t) に戻す、ラプラス逆変換が存在します。
◆ f(t) は、時間 t の世界、すなわち、われわれが生活している世界です。これに対して、F(s) は、s という関数の世界であり、別の世界です。時間 t の世界のことを「時間領域 」、関数 s の世界のことを「ラプラス変換領域 」と呼んでいます。
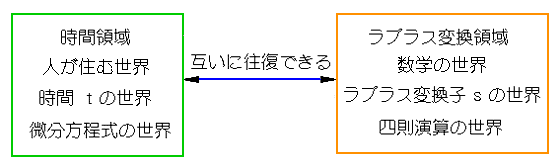
◆ 時間領域とラプラス変換領域とは、ラプラス変換およびラプラス逆変換によって、相互に、任意に、往復することができます。時間領域で微分方程式を含んでいても、ラプラス変換領域に移れば、加減乗除の4則演算だけで処理可能な世界です。
このラプラス変換領域で、うまく変形しておいてから、時間領域に戻ることによって、微分方程式は、4則演算だけで解くことができます。
制御の問題は、微分方程式を解く必要すらありません。もっと簡単に処理できます。
◆ 制御の問題は、伝達関数 と呼ばれるもの利用して、簡単に、解析、設計を行うことができます。
時間関数で表わされた制御要素は、一般に遅れを伴います。すなわち、微分方程式を含んでいます。これをラプラス変換すれば (これは単に、 d/dt→s の置き換です) 、微分記号は無くなって、4則演算だけで処理できます。
これを変形して、伝達関数という関数を導入します。この伝達関数を使用すると、ラプラス変換領域において、入力 X(s) に伝達関数 F(s) を掛け算したものが、出力 Y(s) になるという、非常に簡単な形で表わすことができます(図 3-1-6)。
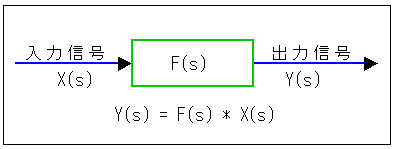
[注] 乗算記号は、× を使うとX(エックス)と紛らわしいので、コンピュータプログラムで使用する、* を使用しています。
◆ 簡単な例 (RCフィルタ) で示しましょう。まず、コンデンサ C 単体を図 3-1-7 に示します。
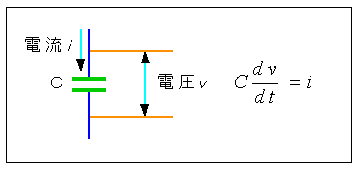
◆ コンデンサの電圧と電流との関係はインピーダンス です。しかし、別の表現として伝達関数の形で表わすことができます。
図 3-1-7 の式をラプラス変換すると、微分記号 d/dt をラプラス変換子 s に置き換えれば良いわけですから、式 3-1-2 になります。
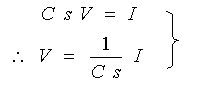・・・ (3-1-2)
この式で、1 / C s が伝達関数です。
伝達関数は s の関数です。電流を入力、電圧を出力として、入力に伝達関数をかけたものが出力、すなわち電圧になっています。
コンデンサの電流と電圧の関係は、インピーダンスで表され、その値は 1 / jωC です。伝達関数を求めれば、インピーダンスは、
s→jω
と置き換えることによって得られます(理由は3.1.2.(3)に示します)。
◆ 次に、RC フィルタを図 3-1-8 に示します。
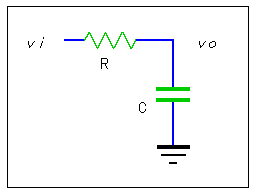
◆ 図から、
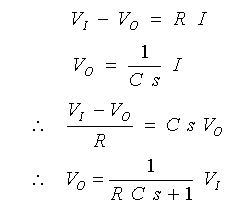・・・ (3-1-3)
となります。すなわち、RCフィルタは、時定数 T = RC として、伝達関数 1 / (Ts + 1) で表わすことができます。
[注1]
2.1.6.(1-A) テスト回路-2 (TST02.CIR) の、回路(0)〜(2)の RC回路を伝達関数で表したものが式 3-1-3 です。
[注2] 2.2.3.(1-B) リスト2-2-2 に示した、制御対象のサブサーキット PRCS における制御対象は、伝達関数で表わされています。
◆ フィードバック制御の問題では、制御要素を時間領域で表現するときと、ラプラス変換領域で表現するときの両方があります。
同じ制御要素に対しては同じ文字を使用し、時間領域は x(t) のように小文字で、ラプラス変換領域は X(s) と大文字で示します。
このように書くと大変分かりやすくなります。さらに、時間 (t)、ラプラス変換子 (s) を省略して、単に x、X と書いても両者を区別することができます。
この講座でも、これからはこの表現形式を使用します。すなわち、伝達関数は大文字で書きます。
[注] 実は、既にこの章は、この表記法で書かれています。
◆ 制御システムは制御要素の集まりとして表されます。各制御要素は、図 3-1-1 に示したようにブロック図 で表します。
そして、各制御要素の出力と入力とをつないで、信号の流れを表します。
制御要素を伝達関数で表わし、ブロック図の各ブロックの中に伝達関数を記入すると、図 3-1-9 のようになります。
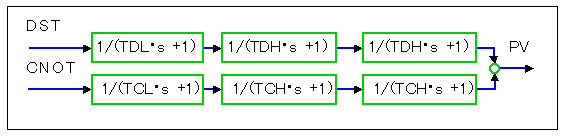
◆ この図は、サブサーキットの制御対象(2.2.2(1-D) 図 2-2-5)を伝達関数の形で表したものです。 この形式のブロック図は、制御システムの流れが、図の形で分かりやすく表現され、かつ伝達関数によって定量的に示されています。制御システムの表記法として優れた方式です。
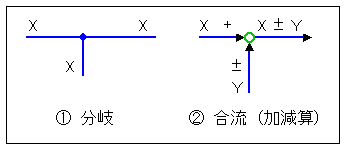
◆ 物質やエネルギの流れの分岐は、量の分配をともないます。しかし、制御では分岐は信号の流れとして扱います。信号は分岐 しても値は変化しません。同じ値が伝わります (図 3-1-10 (1))。
ブロック図において、複数のブロックが合流するときは、加算または減算になります。合流 は図 3-1-10 (2) のように表わします。
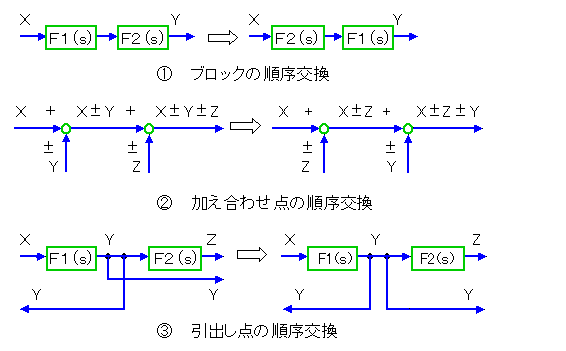
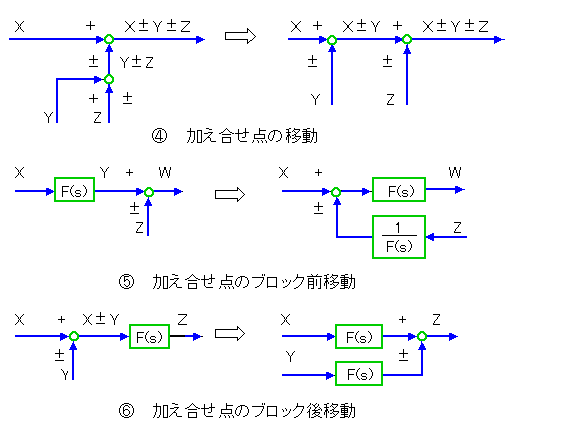
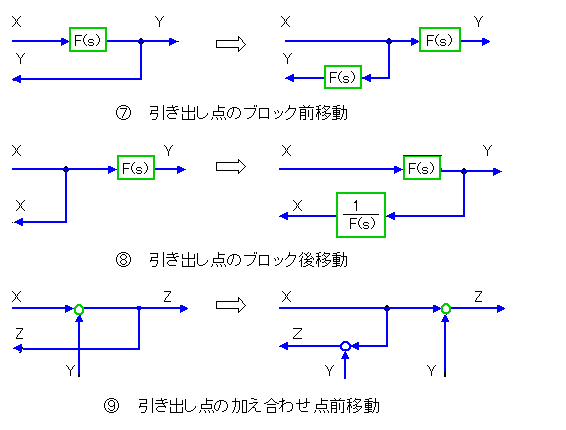
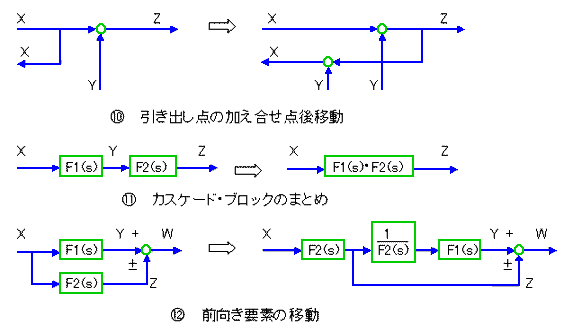
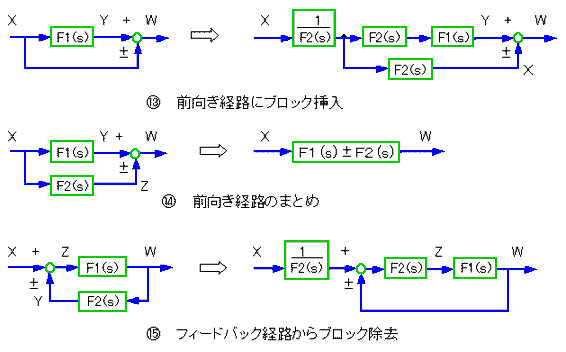
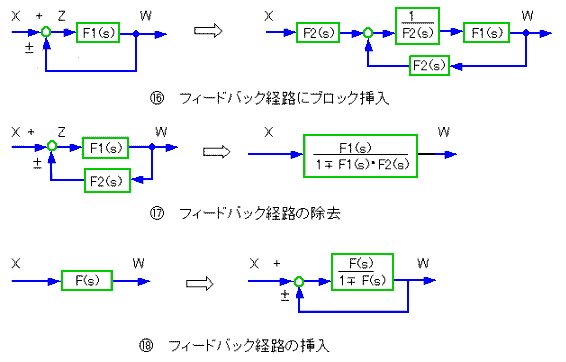
◆ 制御系の解析、設計を行うとき、制御系を伝達関数表示のブロック図の形で表現し、ブロック図を変形して行くのが便利です。
ブロック図の元は代数演算です。代数の法則にしたがって変形することができます。この変形規則を、ブロック図の形で表現したものを、ブロック図の変形法則 と呼んでいます。これを、図 3-1-11に示します。
