◆ 信号が交流のときは、交流増幅器 を使用することが、できます。これから述べる交流増幅器に対して、すでに述べてきた増幅器(図 6.1-7、図 6.1-8)のことを、直流増幅器 といいます(図 6.1-9)(図 4.3-22 参照)。 直流増幅器でも、交流を取り扱うことは、可能です。しかし、直流成分を考える必要が無く、交流だけを検討すれば良い場合には、交流増幅器を使う方が、簡単です。
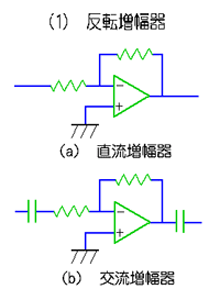
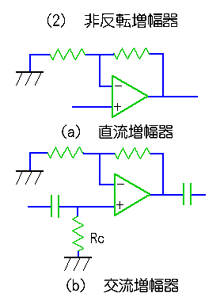
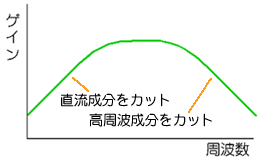
◆ 交流増幅器では、図に示すように、コンデンサで、直流成分をカットします。すなわち、ハイパスフィルタを掛けます。ただし、原理的には、それで良いのですが、耐ノイズ性を高めるために、通常は、図 6.1-10 に示すように、バンドパスフィルタを使用して、周波数帯域を狭くします。増幅器のノイズは、増幅器の周波数帯域が狭い方が、少なくなるからです。
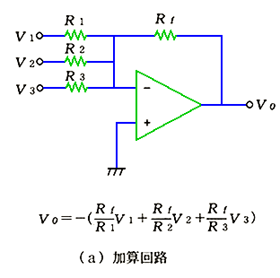
◆ 加算回路 は、アナログ信号の加算を、減算回路 は、アナログ信号の減算を行う回路です(図 6.1-11)。
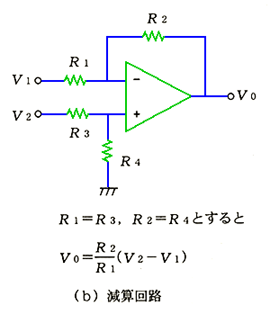
◆ 減算回路は、差動増幅回路(入力値の差を増幅する回路)にもなります。差動増幅回路 は、ノイズ対策用の増幅器です。コモンモードノイズを除去して、ノーマルモード電圧だけを取り出すのに使用します(コラム 6.1-3参照)。
★ モードには、いろいろな意味があります。最も一般に使われているのは、服飾などの流行、ファッションの意味です。

★ 携帯電話で i-モードのモードは、方式の意味です。音楽では、モードは音階です。
★ ノイズでのモードは、現れ方、形態を意味します。ノイズには、コモンモード 、ノーマルモー ドの 2 種類があります。しかし、このコモンモード/ノーマルモードというのは、ノイズだけの用語ではありません。信号一般に関する言葉です。
すなわち、信号には、ノーマルモード信号(電圧)とコモンモード信号(電圧)との 2 種類があります。
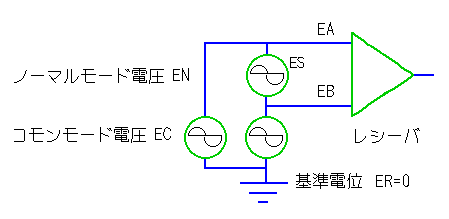
★ 信号は、2 本の線で作る回路を伝わります。上図で、2 本の線は、EA と EB です。信号源は、ES で、この信号源電圧 ES が、2 本の線を、差電圧(EA - EB)として、伝わるわけです。この 2 本の線を伝わる、差電圧信号のことを、ノーマルモード信号、その電圧を、ノーマルモード電圧 EN といいます。
EN = EA - EB = ES
★ この 2 本の線は、基準電位から見ると、ある共通の電圧 EC を持っています。この共通の電圧 EC のことを、コモンモード電圧といいます。2 本の線の電圧が等しくないときは、コモンモード電圧 EC は、
EC = (EA + EB)/2
すなわち、2 本の線の電圧の、平均値で定義されます。
★ 信号を受けるレシーバ は、2 本の線の差電圧、すなわちノーマルモード信号 EN を検出します。レシーバは、原理的には、コモンモード電圧に感じないように作られています。したがって、コモンモード電圧が載っていたとしても、通常は差し支えありません。
★ ここで、レシーバとは、本式のレシーバのことです。通常のディジタル IC の入力は、コモンモード電圧に影響されます。ただし、通常のディジタル IC には、ノイズマージンがありますから、このノイズマージンの範囲内のノイズであれば、誤動作は起こしません。
★ コモンモードノイズ は、通常は、問題になり難いイズです。これに対して、ノーマルモードノイズ は、同じノーマルモードである信号と、区別できません。この意味で、ノイズ対策は、ノーマルモードに対する方が重要です。
★ しかし、この、コモンモードモード電圧は、いろいろな要因によって、ノーマルモードに化けて、ノーマルモードノイズになります。信号は、ノーマルモードです。ノーマルモードに化けたノイズは、信号と区別が付けられませんから、誤差や誤動作に、繋がります。
★ 差動増幅回路は、差動信号、すなわち、ノーマルモードだけを検出し、コモンモード信号には感じません。
★ この差動増幅器を、さらにグレードアップしたものに、計装増幅器 (計装用増幅器 、インスツルメンテーションアンプりファイア )(下図)があります。差動アンプは、コモンモードノイズを除去する効果がありますが、入力が、ハイインピーダンスではありません。
差動増幅回路の前段に、バッファを挿入することによって、増幅器の入力を、ハイインピーダンスにしたものが、計装増幅器です。図に示すように、バッファの入力は、オペアンプの入力、そのものですから、バッファの入力は、極めてハイインピーダンスです(6.1.(4-B-a)参照)。
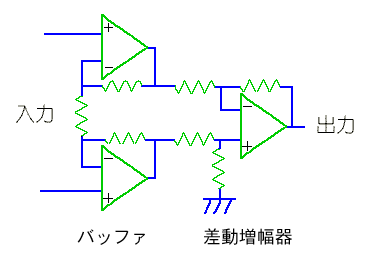
★ この回路は、アナログのオペアンプ回路ですが、バッファの効用は、ディジタル IC のバッファと、ほぼ同じです。それに加えて、オペアンプ回路のバッファは、上記のように、系の入力インピーダンスを高くする効果があります。
★ 差動増幅器においては、増幅器としての入力インピーダンスは、外付けの抵抗の値です。したがって、その入力インピーダンスは、あまり高くはありません(10〜100 kΩ程度)。これに対して、オペアンプ自体の入力インピーダンスは、はるかに高い値です。
★ 信号源インピーダンスが高いときは、増幅器としての入力は、信号源インピーダンスに対して、インピーダンスが、相対的に高くないと、誤差になります。この意味では、増幅器としての入力インピーダンスが高いほうが、望ましいのです。
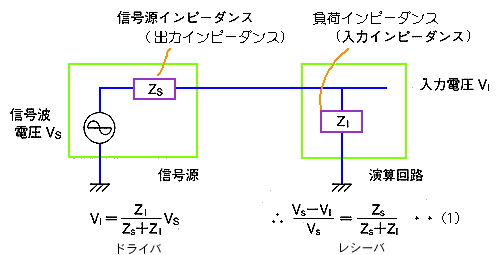
★ 計装増幅器は、この要求を満たすものです。また、2 段増幅になっており、増幅器全体としての増幅率を、2 つの増幅器で分担しますから、高い増幅率が得られます。
★ フィルタについては、これまで、信号が、ノーマルモードであることを前提に、説明してきました。すなわち、これまで説明してきたフィルタは、ノーマルモードフィルタ です(たとえば、図 3.2-5、図 3.2-16 )。
これに対して、コモンモードフィルタが、あります。コモンモードフィルタ は、次のようはフィルタです。
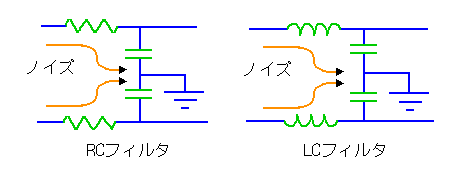
★ コモンモードフィルタでは、図に示すように、中点をグラウンドに落とします。ただし、このグラウンドは、対象としているコモンモードの、戻り道でなければなりません。
また、2 つのフィルタは、特性が揃っていることが必要です。フィルタ特性に差があると、その差の分が、ノーマルモードに化けてしまいます。
★ 上に示したように、コモンモードは、それ自体は、害にならない場合も多いのですが、コモンモードが、ノーマルモードに化けると、有害なノイズに変身します。信号の、往きと、復りの特性が、そろっていれば、コモンモードは、ノーマルモードに化けません。しかし、特性が、等しくないと、コモンモードは、ノーマルモードに化けます。
★ 信号の往きの経路と、復りの経路の特性が、等しいことを、平衡 であるといいます。
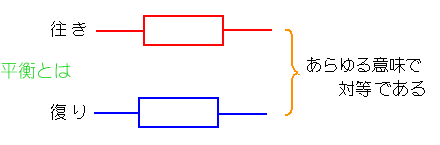
★ 平衡は、コモンモード信号を、ノーマルモード信号に化けさせ無いための、重要な性質です。
平衡で無いことを不平衡 といいます。しかし、平衡は、アナログ的な概念です。ディジタル的に、平衡であるか、無いか、ということではなく、平衡な程度、平衡度 を考える必要があります。
★ 平衡回路と、不平衡回路を、フィルタを例として示します。
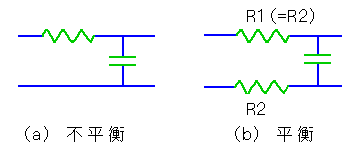
◆
アクティブフィルタ は、トランジスタ増幅回路で作ることもできますが、通常は、オペアンプで構成します。パッシブフィルタは、簡単なことが特徴ですが、シャープな特性を持つフィルタを作ることができません。アクティブフィルタは、特性の優れたフィルタを作ることができます。3.2.(2)では、専ら、パッシブフィルタについて説明しました。ここで、アクティブフィルタについて、解説します。
◆
アクティブフィルタの、もう 1 つの特徴は、インダクタを使用しないで済むということです。フィルタを構成するためには、リアクタンス素子が必要です。リアクタンス素子には、コンデンサとインダクタとがありますが、インダクタは、コンデンサに比べると、寸法が大きく、かつ高価な傾向があります。特性が優れたものが得難いということもあります。
◆
ただし、パッシブフィルタでは、インダクタを使わないと、特性の良いフィルタを作ることができません。
◆
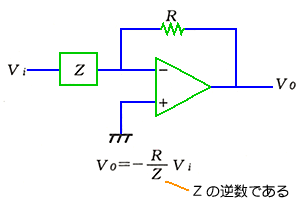
オペアンプ回路で、インダクタを使わないで良い理由は、オペアンプ回路では、容易に、逆数を作ることができるからです(図 6.1-12)。インダクタとコンデンサのインピーダンスは、逆数の関係にあります(図 3.1-1 参照)。
ですから、コンデンサだけで、パッシブフィルタの、LC フィルタなどと、同じ特性のフィルタを、作ることが、できます。
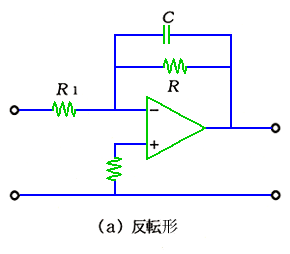
◆
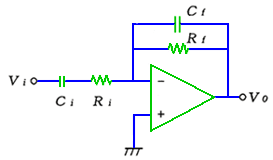
(a)は、反転形 1 次ローパスフィルタ です。カットオフ周波数 fc は、
fc = 1 / (2π C R)
通過域のゲイン A は、
A = R / R1
です。
◆
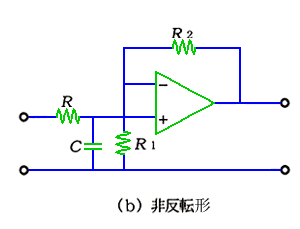
(b)は、非反転形 1 次ローパスフィルタで、カットオフ周波数は、反転形と同じです。通過域のゲイン A は、
A = 1 + (R2 / R1)
です。
◆
1 次ローパスフィルタの周波数特性は、 図 3.2-11の緑 を、過渡特性は 図 3.2.12 の緑を参照してください。
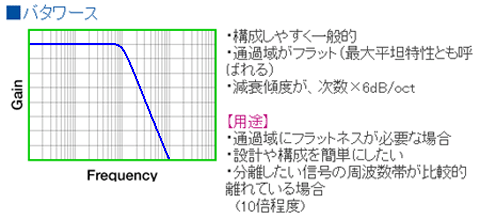
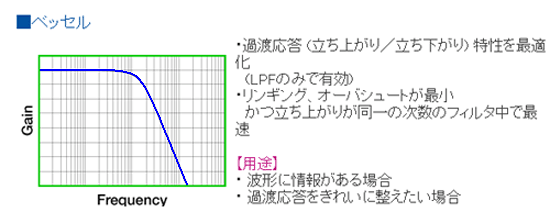
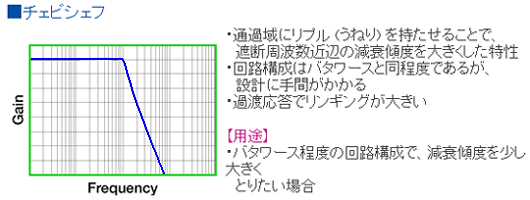
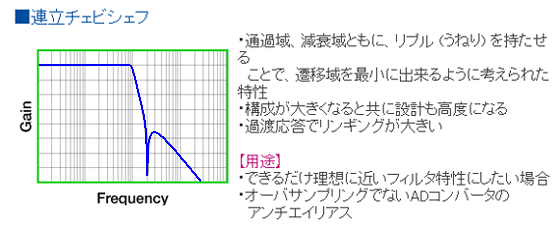
◆ 1 次ローパスフィルタは、パッシブフィルタも含めて、周波数特性の形が決まっています。これに対して、2 次ローパスフィルタ (および 2 次以上)の特性は、各種のものが作れます(図 6.1-14)。代表的なものに、バタワース 、ベッセル 、チェビシェフ 、連立チェビシェフ があります。

◆ 図に示した、各々のフィルタの概略の特性を、図 6.1-15 に示します。図の特性は、2 次フィルタではなく 4 次フィルタですが、傾向は同じです。また、説明中に、まだ説明していない用語が入っていますが、分からなければ、読み飛ばしてください。
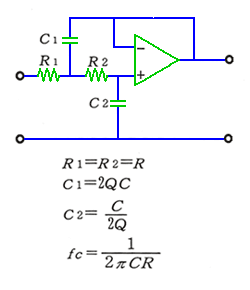
◆ 図 6.1-16 は、2 次ローパスフィルタの代表的な回路で、サレンキー形 と呼ばれている回路です。
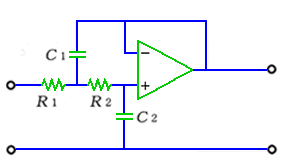
◆
サレンキー回路の、カットオフ周波数 Fc は、
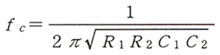 ・ ・ ・ (1)
・ ・ ・ (1)
です。
◆
2 次(またはそれ以上の)フィルタには、共振の現象があります。共振の程度を決めるのが、Q です。サレンキー回路の Q は、
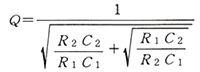 ・ ・ ・(2)
・ ・ ・(2)
で、与えられます。これを図にしたのが、図 6.1-17 です。
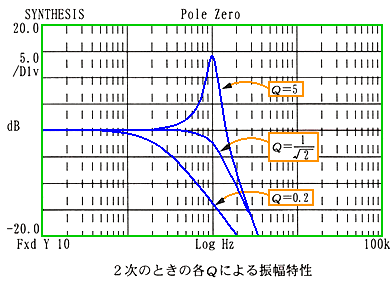
◆
サレンキー回路においては、バタワース特性のとき、
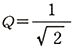
で、ベッセル特性のとき
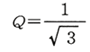
となります。
◆
Q を決めれば、フィルタの定数は、(1)式と(2)式から、
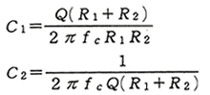
となります。ここで、実際に抵抗を選ぶときは、R1 = R2 = R とおくと計算が簡単です。
◆
以上から、図 6.1-18 が得られます。図のように、2 次フィルタを表記することを、正規化 といいます。