◆ 3 次ローパスフィルタ は、図 6.1-19 に示すように、1 次ローパスフィルタと、2 次ローパスフィルタとを、組み合わせて作ることができます。
◆
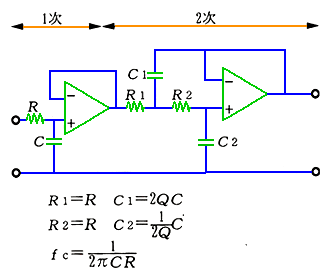
3 次バタワースフィルタの Q は、
1 次 : Q ＝ 0.5
2 次 : Q ＝ 1
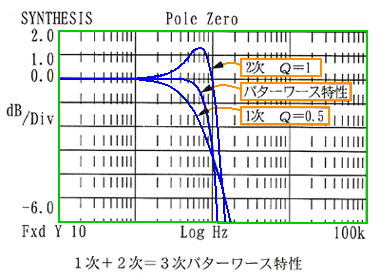
です。このときの、1 次と 2 次のフィルタの周波数特性は、図 6.1-20 の通りです。図を見ると、1 次フィルタの特性が、だれているところを、2 次フィルタのピークが、ちょうどうまく、補正していることが、分かります。
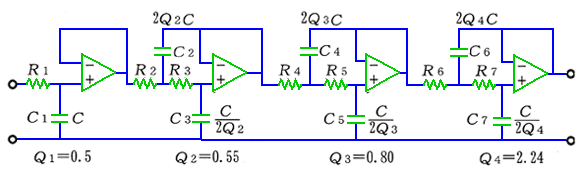
◆ さらに、高次の高次フィルタ も、1 次フィルタと、2 次フィルタとの組み合わせで作ることができます。図 6.1-21 は、7 次フィルタの例です。
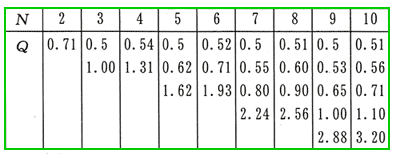
[図 6.1-22] バタワース特性の Q (N : 次数)
◆ 7 次バタワースローパスフィルタの周波数特性を、図 6.1-23 に示します。
[図 6.1-23] 7 次バタワースローパスフィルタの周波数特性
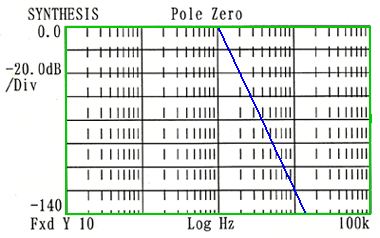
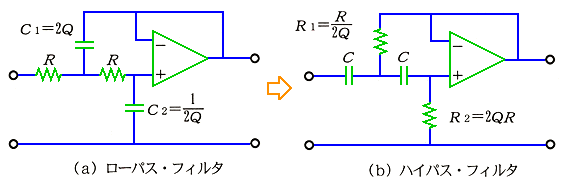
◆ 以上、ローパスフィルタについて、説明してきましたが、ハイパスフィルタについても、同様です。図 6.1-24 のように、ローパスフィルタと、ハイパスフィルタとが、対応します。ハイパスフィルタの設計は、まず、ローパスフィルタを設計してから、それを、図のように置き換えるのが、便利です。
[図 6.1-24] ローパスフィルタとハイパスフィルタとの対応
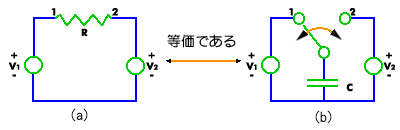
◆ 図 6.1-25において、コンデンサに接続したスイッチを、高速で切り換えると(図の b)、それが等価的に、抵抗として働きます(図の a)。このことを利用した、フィルタを、スイッチトキャパシタフィルタ といいます。スイッチトキャパシタフィルタのことを、以下 SFC と呼びます。
[図 6.1-25] スイッチトキャパシタフィルタ(SFC)の原理
◆
SFC で、スイッチを(1)側に倒して充電するときの、電流 I は、Q を電荷、T1 をスイッチが(1)側に倒れている時間とすれば、
I ＝ Q / T1
です。
◆
スイッチが(2)側に倒れている時間 T2 を T1 と等しくすると、充電と放電の平均電流の値は、同じになります。C : コンデンサのキャパシタンス、f : スイッチング周波数 とすれば、Q ＝ CV (キャパシタンスの定義、2.2.(4-C-a)参照)、T1 ＋ T2 ＝ T ＝ 1/f ですから、
I ＝ V ・ C ・ f
さらに変形すると、
1 / (C ・ f) ＝ V / I ＝ R
となり、1 / (C ・ f) は、等価的に、抵抗 R となります。
◆
SFC は、この等価抵抗 R と、キャパシタンス C とで、フィルタを形成したものです。図 6.1-26 は、SFC による、1 次ローパスフィルタです。
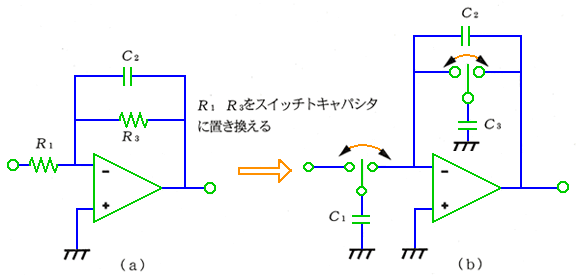
◆ SFC は、容易に、IC に集積することが、できます。ディジタル回路における、FPGA のように、SFC を多数集積した素子を、FPAA といいます。
★ バタワース、チェビシェフなど、フィルタの名前は、そのフィルタを考え出した、数学者の名前です。このことからも、フィルタが、難解なものであることが、推測されます。
★ 数学者たち によって、いろいろなフィルタが、考え出されましたが、万能な、理想的なフィルタは、世の中に存在しません。目的用途によって、使い分けることになります。
★ 本文では、アナログ回路のフィルタについて、説明しています。しかし、最近では、信号を、ディジタル化して、コンピュータソフトウェアのフィルタを使うことが、多くなっています。これは、フィルタに限らず、一般的な傾向です。信号をディジタル化して、コンピュータ処理することを、信号処理 と、呼んでいます。
★ さて、リゾートとして、マレーシアのペナン島が、有名です。
★ ペナン島は、マレーシアの西海岸、バンコックとシンガポールとの、中間にあります。この、ペナン島の対岸、本土側の町が、バタワースです(下図右上がバタワース駅)。バタワースからペナン島へは、フェリーが頻繁に通っています。
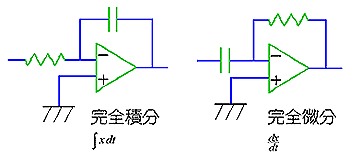
★ 積分回路 と微分回路 は、積分と微分の演算を行う回路です。ただし、通常、積分回路、微分回路と呼ばれているものは、純粋な積分や、微分の演算を行うものだけでなく、類似の動作を行うのものを含んだ、名称です。
★ 純粋な積分回路のことを完全積分回路 、純粋な微分回路のことを完全微分回路 と呼んでいます。完全積分回路/完全微分回路に対して、通常、積分回路、微分回路と呼んでいるのは、正確には、不完全積分回路 /不完全微分回路 と呼ばれるものです。
★ 不完全積分回路は 1 次ローパスフィルタと、不完全微分回路は 1 次ハイパスフィルタと同じものです。
★ これらの周波数特性は、下図のとおりです。
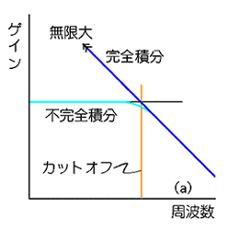
★ 不完全積分は、低い周波数帯域では、ゲインが頭打ちになりますが、高い周波数帯域(図の(a))では、完全積分と同様に利用できます。
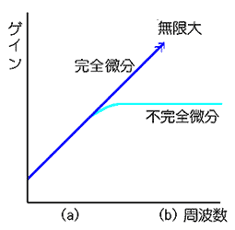
★ 完全微分は、実用になりません。完全微分のゲインは、高周波で無限大になります。ところが、一般にノイズは、信号よりも高い周波数で多くなります。このため、完全微分は、ノイズ増幅器になってしまい、使い物にならないのです。
★ 微分特性は、不完全微分回路を使用し、(a)の部分を利用します。(b)の周波数帯域で、ゲインは頭打ちになります。ノイズ対策として必要なことですが、その分、微分効果は減殺されます。これは、やむをえない、ことです。通常は、20 dB で頭打ちになる条件で使用します。
◆
ダイオードは、非線形です。したがって、ダイオードを利用して、各種の非線形を作ることができます。しかし、ダイオード自身は、非線形としての典型的な、すなわち、理想的な特性は、持っていません(ダイオードの現実特性は、図 4.2-3)。
ダイオードを、オペアンプと組み合わせることによって、理想的な特性を持つ非線形回路を作ることができます。
◆
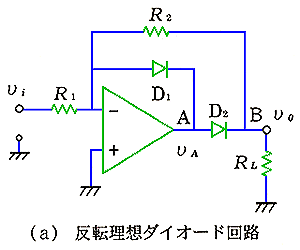
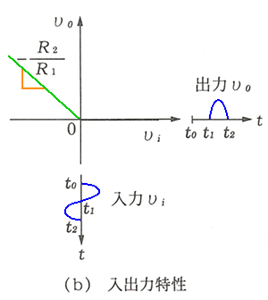
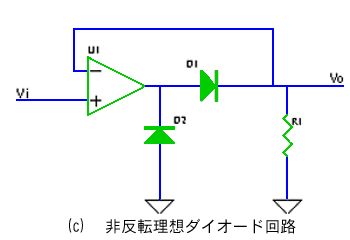
その第 1 が、理想ダイオード です。ダイオードは、非線形特性をもち、その特性を利用します。しかし、現実のダイオードは、理想的な特性を持っていません。ダイオードをオペアンプと組み合わせることによって、理想的な特性を作ることができます(図 6.1-27)。図の(a)は、反転形、(b)は、その特性、(c)は、非反転形です。なお、ダイオード D1、D2 の向きを変えると、理想ダイオードの向きが変わります。
◆
この回路は、フィードバックのところに、ダイオードが入っています。このような回路であっても、正常な動作状態においては、仮想短絡、仮想接地が成り立ちます。したがって、オペアンプの反転入力端子の電圧は、グラウンドレベルです。また、入力抵抗 R1 に流れる電流と、フィードバック側に流れる電流の大きさは、等しくなっています。
ただし、ダイオードがスイッチとして働きますから、電圧の掛かる方向によって、電流の経路が異なります。
◆
(a)の反転形について、その動作を説明します。まず、入力電圧 vi が正のときを考えます。このときは、抵抗 R1 を通って、電流 i が、反転入力端子の方向に向かって流れ込みます。この電流は、オペアンプ出力 A への電流になります。ダイオード D1 を流れる経路と、ダイオード D2 を流れる経路の、2 通りがありますが、D1 の経路は順方向、D2 の経路は逆方向です。
◆
したがって、D1 だけに電流が流れ、抵抗 R2 には、電流は流れません。その結果として、抵抗 RLにも、電流は流れませんから、B 点の電圧は、ゼロです。このとき、オペアンプの出力電圧vAは、ダイオードの順方向電圧によって、約 0.6 V です。
◆
入力電圧 vi が負のときは、オペアンプの出力 A 点から、反転入力端子の方に電流が流れます。したがって、ダイオードに掛かる電圧は、上記と逆ですから、ダイオード D1 には電流が流れないで、ダイオード D2、抵抗 R2 を通って電流が流れます。このときは、R1 とR2 とを流れる電流は等しいですから、B 点の電流について、
vo ＝ −(R2/R1)・Vi
が成立します。以上を総合すると、図の(b)のようになります。
◆
(c) の非反転形については、各自で、辿って見てください。
◆
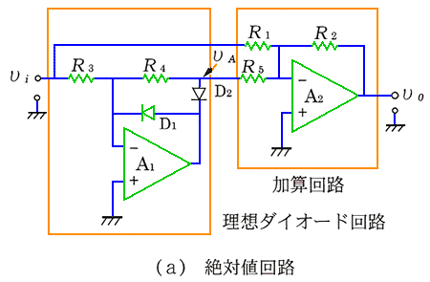
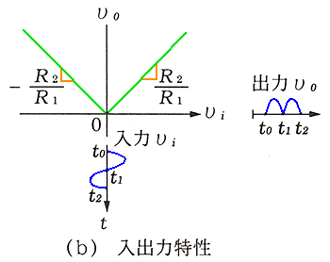
理想ダイオード回路と、加算回路とを組み合わせると、絶対値を求める、絶対値回路 を作ることができます(図 6.1-28)。絶対値回路は、全波整流と同じ動作です。抵抗値は、
(R1 ・ R4) / (R3 ・ R5)
となるように、します。
◆
入力信号が、正のときを考えます。出力 vo は、入力 vi と理想ダイオードの出力 vA とを加算したものです。その結果は、次のようになります。
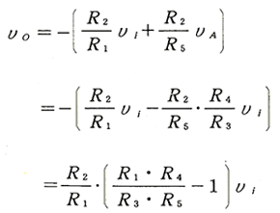・ ・ ・ (1)
◆
一方、vi が負のときは、出力 vA ＝ 0 V なので、
vo ＝ −(R2 / R1) vi
となります。したがって、(1)式において、
(R1 ・ R4) / (R3 ・ R5) ＝ 2
とすれば、vo は、
vo ＝ (R2 / R1) ・ | vi |
となり、絶対値が求まります。
◆
負の絶対値は、図の(a)の、2 つのダイオードを逆向きにすれば、
vo ＝ −(R2 / R1) ・ | vi |
となり、負の絶対値が、得られます。
◆
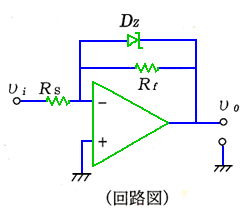
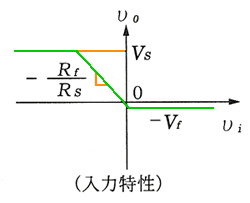
パッシブのリミッタについては、4.2.(3-B)に示しました。ここでは、ツエナダイオードによる、アクティブのリミッタ について説明します。ツエナダイオードは、ダイオードの降伏による、ツエナ電圧が、ほぼ一定である性質を利用して、定電圧を作るのに利用されています。
◆
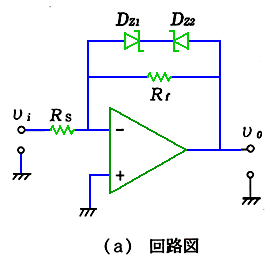
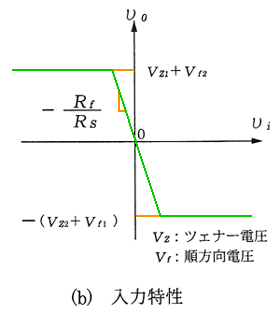
図 6.1-29 は負電圧入力のリミッタ、図 6.1-30 は両方向電圧入力のリミッタです。
