◆ 抵抗などの素子は、単体で使用されることはありません。複数の素子を互いに接続し、回路を組んで使用します。たとえば、図 2.1-4 は、単純ですが、回路を構成しています。回路 は、回の字が示すように、一回りする路です。図 2.1-4 を見ても、ぐるっと、電気が、1 巡しています。回路は、一般に、電線で構成されますから、回線 という言葉も使われます。
このように、電気回路は、閉じたループを描いていなければなりません。これによって、電子は、ぐるぐる回って、仕事をすることができます。水路の途中に障害物を入れれば、水は流れません。水を流し続けるためには、水路が、ぐるっと一巡して、つながっている必要があります。これと同じです。
さらに、水を流すための力も必要です。タンク B からタンク A に揚水するためには、ポンプが必要です。
◆ 自由電子は、自由に動き回りますが、全体を平均すれば、同じ位置にあります。一定の方向に電子を回らせるためには、図 2.1-4 に示したように、電池/発電機などの、電源が必要です(図 2.1-12)。
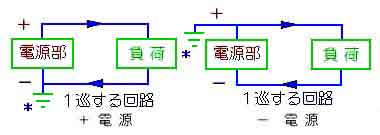
◆ 以上から、回路は、実際に仕事(ここの仕事は一般的な意味の仕事です)をする部分と、この部分が仕事をするために必要な電圧を発生する電源 部とが、必要です(図 2.1-13)。電源の供給を受けて動作する部分を、電源に対して、負荷 と呼んでいます。
電源には、プラス電源とマイナス電源とがあります。グラウンド(図の * のところにある記号)を基準として、電源の出力が、プラスのものをプラス電源 といい、マイナスのときがマイナス電源 です。
◆ 図 2.1-3 では、水が回っています。図のように、回すためには、電気で電源部が必要であったように、ポンプが必要です。
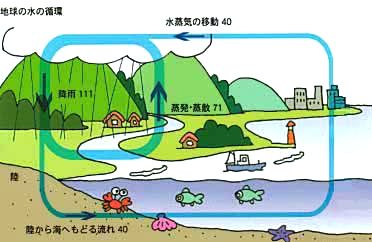
自然の水も、大きく回っています(図 2.1-14)。自然の水を回すための動力は、太陽エネルギーです。すなわち、太陽光を受けて、水面などの水が蒸発し、蒸発した雲が、雨や雪になって、再び地上に戻ってきます。
◆ 複数の抵抗を、つないだ回路を、作って見ましょう(図 2.1-15)。これらの図は、抵抗内部の電圧変化の様子も、示してあります。(a) は、単体の抵抗です。抵抗の内部では、電圧は、連続的に低下しています。
抵抗を、図の(b)のように、接続する方式を、直列接続 と言います。(c) の接続方式を、並列接続 といいます。
◆ (b) 直列接続では、抵抗 R1 と抵抗 R2 に流れる電流は、等しく、I1 = I2 です。図のように、全体に掛かる電圧が分割され、途中の b 点の電圧は、a 点の電圧と、c 点の電圧との中間の値になります。このとき、
・ ・ ・ ・ (2.1-2)
が成立します。ただし、Vac は、a、c 間の電圧です。
Vbc は、Vbc = I R2 = (Vac / (R1 + R2)) R2 = (R2 /(R1 + R2)) Vac と変形できますから、
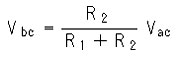・ ・ ・ ・ (2.1-2)´
となります。このように、2 つの抵抗の中間から、中間の電圧を取り出すことを、分圧 といいます。
(c) 並列接続では、抵抗 R1 と抵抗 R2 の両端に掛かる電圧は等しく、どちらも、Va - Vb です。全体の電流 Ia ( = Ib ) は、抵抗 R1 と抵抗 R2 とに分流し、抵抗 R1 に流れる電流 I1 と抵抗 R2 に流れる電流 I2 は、
・ ・ ・ ・ (2.1-3)
となります。
◆ 多数(図では 4 つ)の抵抗を直列接続して見ましょう(図 2.1-16)。この図は、電源を接続して、回路を構成しています。この図によって、回路の基本的な性質を示します。図の＊印の部品は、電池です。電池の図記号は、細くて長い方が プラス 太くて短い方が マイナス です。
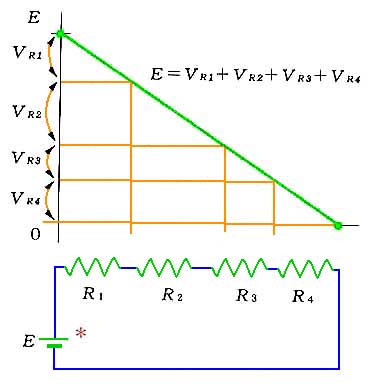
(1) 流れ出した電流と戻ってくる電流の値は、等しい値です。この図は、直列接続だけですが、途中で分流があったとしても、再び合流して、必ず元の値になります。
(2) 結線された部分(途中に素子が無い部分)の電位は等しい値です。これは図 2.1-14 (c)を含めて図を眺めてください。厳密には、配線にも、抵抗があります。しかし、回路図では、配線の抵抗は、ゼロとみなします。
(3) 回路中の電圧降下の総和は、電源電圧に等しくなります。このことは、回路中には、電圧を持ち上げる電源と、電圧を下げる回路素子(負荷)とがあって、回路を一周すれば、ゼロに戻ることを意味しています。電源が複数であっても、電源電圧の総和を考えれば、それが、回路中の電圧降下の総和と、等しくなります。
◆ 複数の抵抗を接続した場合は、以上の通りですが、これをまとめると、次のようになります。なお、ここでは、オームの法則から、式によって、結果を誘導しています。
(1) 直列合成
図 2.1-14 (b) において、I1 = I1 です。これを、Iac とおけば、オームの法則によって、
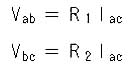・ ・ ・ ・ (2.1-4)
となります。これを、(2.1-2) 式に代入すれば、
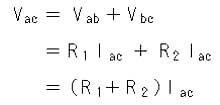・ ・ ・ ・ (2.1-5)
です。このことは、抵抗 R1 と R2 とを直列に接続したときは、(R1 + R2) の値を持つ 1 つの抵抗と、等価であることを表しています。
◆ (2) 並列合成
図 2.1-14 (c) において、抵抗 R1 と抵抗 R2 において、それぞれ、次の式が成立します。
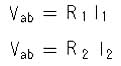・ ・ ・ ・ (2.1-6)
一方、2 つの抵抗の代わりに、a b 間に 1 つの抵抗 R があるとすれば、
・ ・ ・ ・ (2.1-7)
ただし、Iab は、(2.1-3) 式の、Ia です。これらの式から、各電流は、
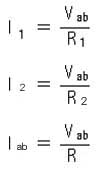・ ・ ・ ・ (2.1-8)
となります。これを、(2.1-3) 式に代入すると、
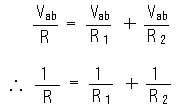・ ・ ・ ・ (2.1-9)
◆ この式が、抵抗の並列合成です。とくに、抵抗が、2 個の場合には、
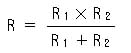・ ・ ・ ・ (2.1-10)
となります。
◆ なお、抵抗の並列合成を、演算記号 // で表して、
R ＝ R1 // R2
のように書きます。この演算記号 // は、電気の分野では、普通に使われている記号ですが、正規の数学記号ではありません。
★ 世の中には、無ければ無いでも済ませられますが、あると便利なものがあります。下図左は壜の栓開け、右は皿吊り です。
★ これから、お話する法則や定理も、それを知らなくても、オームの法則を使って、しこしこ計算すれば、答えを求めることができます。しかし、手間ひまが掛かります。まさしく、使うと便利なものです。
★ (1) キルヒホッフの法則
複雑な回路は、網目のようになっています。このことから、複雑な回路のことを、回路網 (ネットワーク )と呼んでます。回路網の中で、いくつかの導線が集まっているところを、節点 (ノード )といいます。節点に流れ込む電流の和は、ゼロです。ただし、電流は、その向きによってプラス/マイナスの符号を付けます。
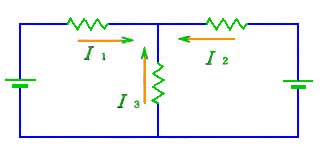
★ また、回路網の中で、任意の閉じたループに沿って一周したとき、ループ内の、起電力の和と、電圧降下の和は、等しくなります。起電力 とは、電流を流し続けようとする作用、たとえば電池のような、電圧を発生し続ける作用のことです。
ここで、注意しなければならないのは、R3 に流れている電流は、R3 に実際に流れている電流 (I1 + I2) を使用することです。注目しているループに関する電流 I1 ではありません。
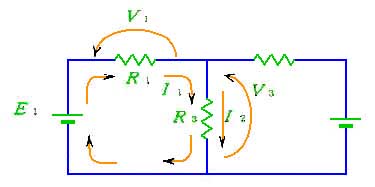
★ (2) 重ねあわせの定理
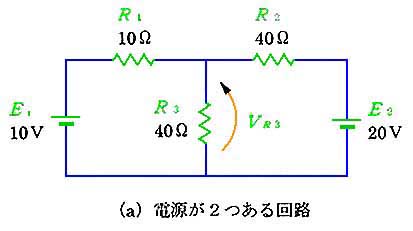
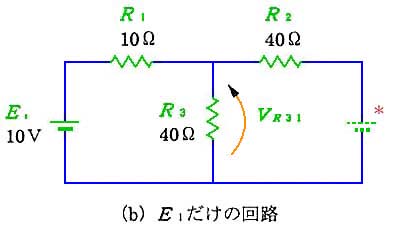
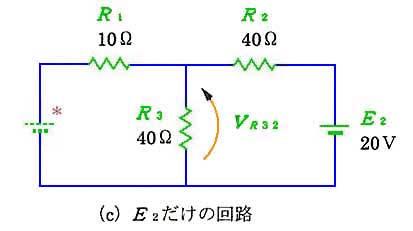
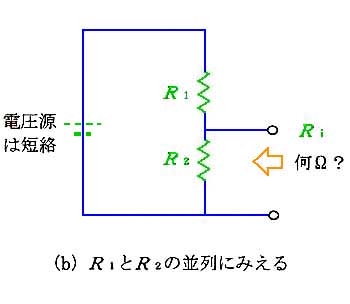
回路の中に 2 つの電源があるとき、または 2 つの信号が同時に入力されたときなどに、使用します。(a) のように、電源が 2 つある回路は、(b) の回路と (c) の回路を重ね合わせたものになりますす。2 つに分けるとき、電源は、図の＊ように、ショートします。
★ (3) 電源
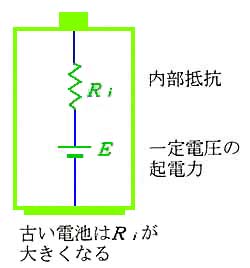
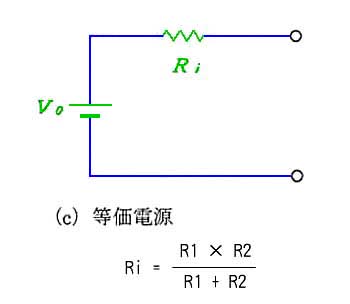
電池などの電源は、理想的な、一定電圧を発生する部分と、電源の内部抵抗とで表すことができます。実際には複雑な回路を、それと同等な動作をする、簡単な回路で表現したとき、その簡単な回路のことを、元の回路の等価回路 といいます。たとえば、等価回路が、1 つの抵抗で表されるときは、等価抵抗 のように、呼びます。
★ 電池を等価回路で表すと、図のようになります。等価回路では、一定電圧を発生する電源のような、実際には存在しない、理想的な動作をする素子を考えることがあります(コラム 3.2-5)。
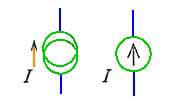
★ このような、一定の電圧を発生する、電源を、定電圧源 といいます。定電圧源の回路図記号は、一般に、電池と同じ記号を使用します。したがって、電池の記号は、実際の電池を表すときと、定電圧源を表す場合の両方があるとに、注意してください。このコラムでは、以降は、電池の記号は、定電圧源です。
逆に、一定の電流を発生する電源も考えることができ、これを定電流源 といいます。定電流源の回路図記号は、次の通りです。
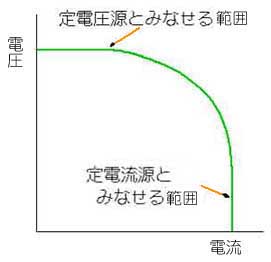
★ 一般の電源は、下図のように、定電圧源と定電流源との、中間の特性を持っています。定電圧源とみなせる範囲を、十分に広く取ったものが、定電圧源、定電流とみなせる範囲を十分に広く取ったものが、定電流源です。
★ (4) テブナンの定理
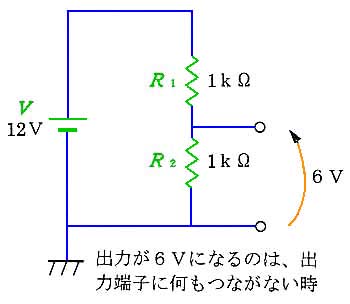
下記のように、電源を抵抗で分圧して、中間の電圧 6V を取り出したいことがあります。しかし、負荷をつなぐと、負荷に電流が流れ、出力端子は、6V では無くなってしまいます。
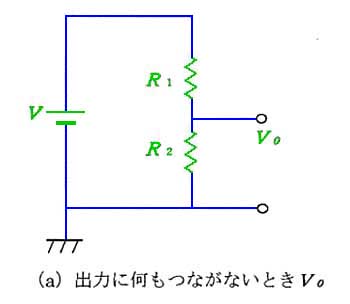
★ それでは、この回路の出力端子の電圧は、いくらになるのでしょうか？ これを計算すのは、かなり面倒です。このようなとき、テブナンの定理が、役に立ちます。テブナンの定理によれば、下図において、(b) の←から見た等価回路が (c) になります。
★ 定理について
このコラムでは、定理がいくつか出てきました。コラム 2.1-4 で、電気の現象で定理が成立することは、ほとんど考えられないと書きました。これと、矛盾するようです。
このコラムの定理は、数式自体は、数学的に証明できます。その数式が、電気の現象を説明しているのです。数式自体が、証明できるので、定理と呼んでいるわけです。電気の現象、それ自体が、証明できるのでは、ありません。
◆ 抵抗に電流が流れると、抵抗でエネルギーを消費します。このエネルギーは、100% 熱 になります。これをジュール熱 といいます。発熱 も仕事です。したがって、発熱量 の単位は、仕事と同じで、[J ジュール]です。
抵抗の発熱作用を利用したものが、電熱器 で、電熱器とやかんを組み合わせたのが、電気ポットです(図 2.1-17)。
◆ 発熱に関しては、ジュールの法則があります。ジュールの法則 は、電位差が、V [V ボルト]、である 2 点間に、I [A アンペア] の電流が、t [s 秒] 間流れたときの発熱量 Q [J ジュール] は、
・ ・ ・ ・ (2.1-11)
です。なお、発熱量の別の単位として、食品で多く使用されているカロリー があります。1 cal (カロリー)は、4.18605 (≒ 4.2) J (ジュール)です。
◆ ここで、電力についても、示しておきます。電力 (パワー )は、電流が、1 秒当たりにする仕事量で、その単位は、P [W ワット ]です。V [V ボルト]、I [A アンペア]、R [Ω オーム] とすれば、
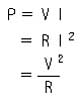・ ・ ・ ・ (2.1.12)
です。また、電力量 は、電力に時間をかけたもので、仕事量の単位になります。多く使われているのは、時間に h (時間 = 60 分) を使用した、kWh です。これを計るのが、電力量計 (積算電力計 )です(図 2.1-18 )。どこの家庭にもある、電気のメーターです。
◆ 電気部品には、定格があります。部品の定格とは、その部品の使用条件(主に使用限界)を定めたものです。
抵抗の仕様にも、定格があり、定格以内で使う必要があります。抵抗の定格には、電圧定格 と、電力定格 とがあります。電圧定格は、その抵抗を使用できる最大の電圧です。
◆ 定格電力は、その抵抗で許容される、電力の最大値です。定格電力は、、抵抗の発熱により、抵抗の温度が上昇するのを、一定以下に押さえるためのものです。しかし、温度上昇は、抵抗が置かれている周囲条件によって、異なります。たとえば、抵抗を近接して並べて配置すれば、温度上昇が大きくなります。したがって、定格を守れば、それで十分ということでは、ありません。定格は、その定格で規定した条件における値です。使用条件によっては、定格値よりも低い条件で、使用する必要があります。
◆ 抵抗の温度上昇は、その抵抗自身だけでなく、周囲の部品を加熱して、影響を与えます。
★ 最近は、電灯は蛍光灯が多くなっています。白熱灯は、効率が悪いので、あまり多くは使われません。しかし、蛍光灯では得られない、温かみを持った色合いが、愛されています。
★ 照明 の色合いは、色温度によって測られます。黒体 (外光を反射しない物質)の温度を上げていくと、発光します。この発光する色は、温度が低いときは赤く、温度を上げるにつれて、橙、黄、白、青みがかった白、と変化します。この色と温度との関係のことを、色温度 といいます。
各種の光源と、その色温度を、次に示します。
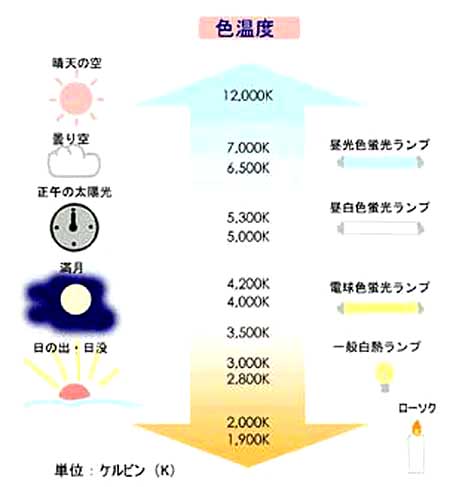
★ 光源の色温度は、人の気分に影響を与えます。ただし、色温度だけでなく、照度(明るさ)と関連します。これを、クルーゾフ効果といいます。
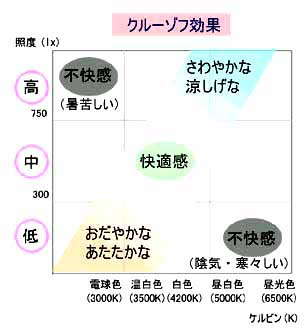
★ 高い照度の蛍光灯は、昼光色を使うことによって、快適感が得られます。逆に、暗い照明では、ローソクの光が、好まれることも、この図から、理由が分かります。
最近では、安全のためもあって、本物のローソクではなく、ローソク形の電灯が使われています。しかし、この電球が、色温度が高いものであったら、何の風情もありません。白熱灯が、適しています。
★ さて、その白熱灯ですが、電球に加える電圧を 0V から徐々に上げて行くと、フィラメントに流れる電流は増加しますが、その増え方は、
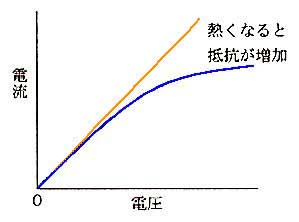
のようになり、飽和の現象があります。これは、抵抗に温度係数があり、温度が高くなると、抵抗値が低くなりからです。各瞬間を考えれば、オームの法則が成立しているのですが、見かけ上、オームの法則に反しているように、見えます。
★ 上記の現象のため、電源を投入したときの、電球のフィラメントの温度が低い状態では、抵抗が低く、大電流が流れて、しまいます。パイロットランプ では、この現象を防ぐために、
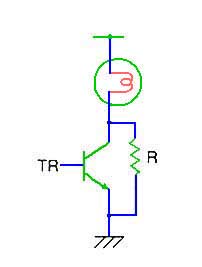
のように、保護回路を入れます。
★ 図で、TR はトランジスタです。このトランジスタは、ランプをオンオフするスイッチです。スイッチオフの状態でも、抵抗 R を通して、常時ランプに電流を流し、ランプのフィラメントを予熱しています。
★ ただし、最近では、パイロットランプに、白熱灯を使うことは、ほとんどありません。白熱電灯は、電力を多く消費し、しかも、寿命が短く、切れやすいからです。パイロットランプは、電力の消費が少なく、かつ、寿命が長い、LED に置き換わっています。
