

◆ フリップフロップは、記憶機能を持った素子であり、順序論理を実現します(図 5.2-64)。

◆
最も基本的なフリップフロップは、RS FF です。RS FF は、レベル (信号が、ハイであるか、ローであるか)で動作します。
RS FF は、フリップフロップの基本ですが、実際に、多く使われいるのは、D FF などの、エッジトリガ タイプです。フリップフロップは、歴史的には、マスタースレーブ と呼ばれる方式からスタートしました。しかし、現在では、マスタースレーブ方式は、使われていません。
◆
フリップフロップは、単体の IC のほか、各種のレジスタや、カウンタ IC の要素として広く使われています。レジスタ とは、複数ビット(通常 4〜8 ビット)のデータを、まとめて、一時的に記憶する素子です(図 5.2-65)。カウンタ は、数を数える IC です。
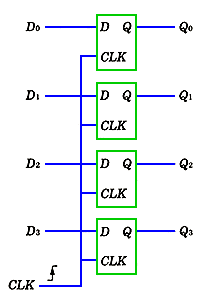
◆ また、フリップフロップと類似のものに、D ラッチがあります。D ラッチについても、説明します(コラム 5.2.5)。
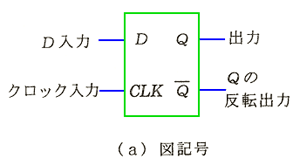
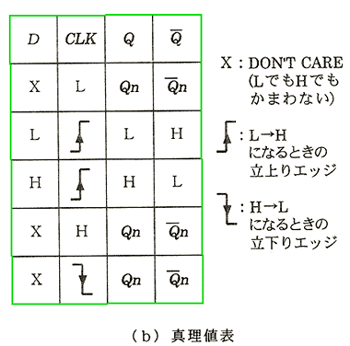
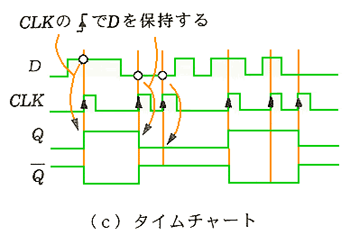
◆ D FF (D フリップフロップ ) は、最も一般的なフリップフロップです。真理値表は、図 5.2-16 に示しましたが、Preset、Clear は、パワオンリセットなどに使用するものであり、D FF の、主動作ではありません。D FF の主動作だけを抜き出した真理値表を、図 5.2-66 に示します。
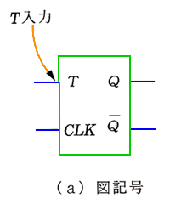
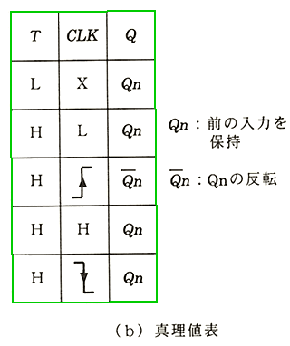
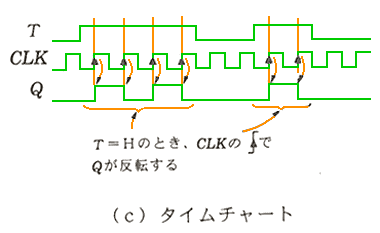
◆ T FF (T フリップフロップ ) を、図 5.2-67 に示します。T FF は、それ自体の IC 製品は、存在しませんが、各種の FF 応用回路の IC に利用されています。
◆ フリップフロップには、セットアップタイム とホールドタイム があります。フリップフロップの動作では、このタイミングを確保する必要があります(図 5.2-68)。
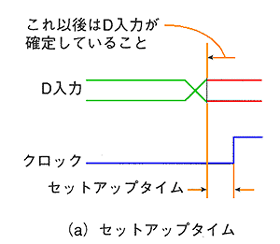
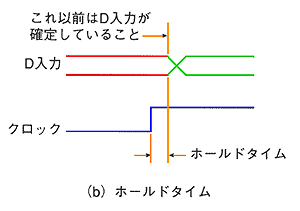
◆ このタイミングが、確保されないと、出力のハイ/ローが、保証されません。すなわち、ハイになるときと、ローになるときとが、あります。通常は、ただ、それだけであって、それ以上の問題は、起こりません。
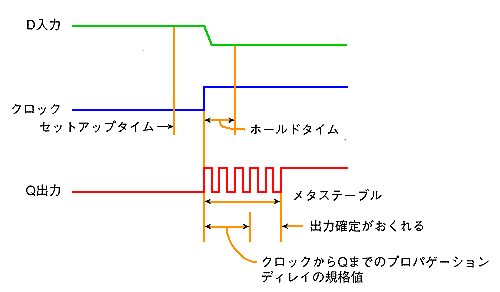
ただし、低い確率ですが、上記のタイミングが、満足されなかったときに、メタステーブル と呼ばれる現象が、発生する可能性があります(図 5.2-69)。メタステーブルは、図に示したように、Q 出力が、バタツク現象です。
◆
メタステーブルは、発生しても、通常は、その時間は、ナノ秒のオーダーです。問題にならずに済むことが、多いのです。しかし、きわめて低い確率ですが、メタステーブルの継続時間が、もっと長くなることがあります。メタステーブルの継続時間が長くて、フリップフロップの規定時間を満足しないと、問題になることが、あります。
◆ メタステーブルは、フリップフロップの、セットアップタイム、ホールドタイムが、満足されなかったときに、発生するのですから、セットアップタイム、ホールドタイムを確保すれば、防止できます。これは、後に述べる、同期式回路を使用すれば、良いのです。同期式回路は、フリップフロップの、セットアップタイム、ホールドタイムを、満足するように、設計することが可能です。
◆ ただし、同期回路であっても、外部からの、最初の入力だけは、同期式に、できないことが多いのです。このような場合には、図 5.2-70 のように、対策します。
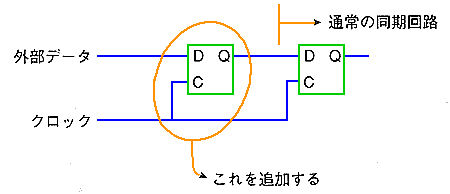
◆ 最初のフリップフロップでは、メタステーブルが発生する可能性が、あります。メタステーブルの継続時間は短いので、最初のフリップフロップでメタステーブルが発生しても、2 段目のフリップフロップにデータを取り込むのは、メタステーブル終了後になります。
ただし、メタステーブルの継続時間が長い確率は、ゼロではありませんから、この回路を使用しても、メタステーブルを 100% 防止することはできません。しかし、メタステーブルを、充分に高い確率で、防止することができます。
◆ なお、追加したフリップフロップによって、1 クロック分遅れますから、この遅れが許容できないときは、この回路は、使用することができません。
◆ カウンタ は、数を数える IC で、フリップフロップ応用製品の代表例です。カウンタは、T FF を複数接続することによって、構成することができます(図 5.2-71)。T FF は、IC がありませんが、図から分かるように、D FF を利用して、T FF を、簡単に作ることが、できます。
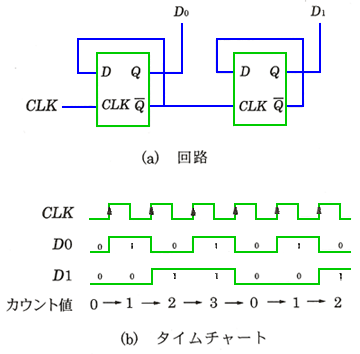
◆ 図は、4 進のカウンタですから、0〜3 とカウントすると、次は 0 に戻り、以下これを繰り返します。このような状態の推移は、タイムチャートでは、十分に表現できません。これを、うまく表現することができるのが、状態遷移図です(図 5.2-72)。
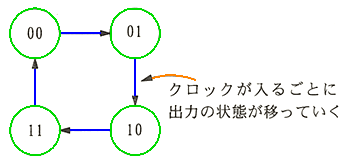
◆
複数のフリップフロップを使用した、順序回路には、同期式回路と非同期式回路の 2 種類が、あります。
同期式 は、注目している回路ブロック内の、全てのフリップフロップのクロックが、同一のクロックで動作する回路です。
非同期式 のフリップフロップは、少なくとも 2 つ以上の異なるクロックで、動作します。
カウンタを例に取ると、図 5.2-73 が非同期式、図 5.2-74 が同期式です。同期式回路では、パワオンリセットなどの、回路を初期化する目的以外には、クリアを使用することは、許されません。プリセットは使用できません。
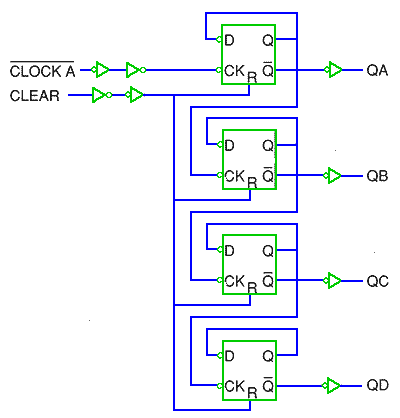
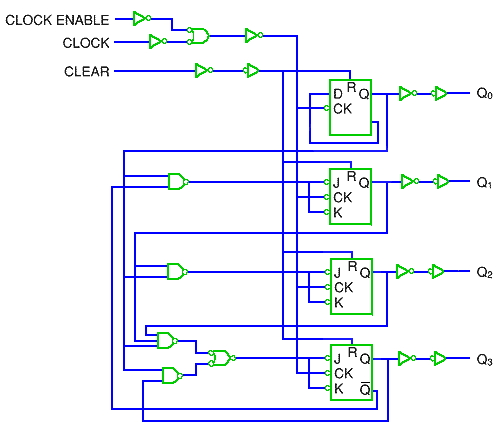
◆
同期式回路と、非同期式回路とを、比較してみましょう。非同期式の特徴は、
a) 設計手法が、確立されていないので、個人の能力や、アイデアに依存する面が、あります。
b) 信号が通過するゲートやフリップフロップの、段数が多くなりがちなので、遅れが大きくなり、高速の回路には、適しません。
c) フリップフロップが、ばらばらに動作します。このため、ノイズなどによって、予期しない状態に陥ったとき、正常状態に、復帰できないことが、あります。
d) 回路規模が大きくなると、a) や c) と同じ理由で、動作の見落としなどを し易く、設計ミスが多くなる傾向があります。
e) ロジックファミリを使用した小規模な回路は、とくに意識して設計しない限り、ほとんどが、非同期式になります。
◆
同期式の特徴は、次の通りです。
a) 回路形式を、定形化できるので、決まった順序で設計できます。このため、個人差ができ難い傾向が、あります。
b) 遅れ時間が規格化されるので、大規模回路でも、高速動作を維持できます。
c) PLD や FPGA(コラム 5.2-3)は、同期式の構成になっています。これらを利用すれば、必然的に、同期式回路になります。
◆
非同期式回路では、以下に示すような、回路要素が、よく使用されます。
ア) 信号遅延回路
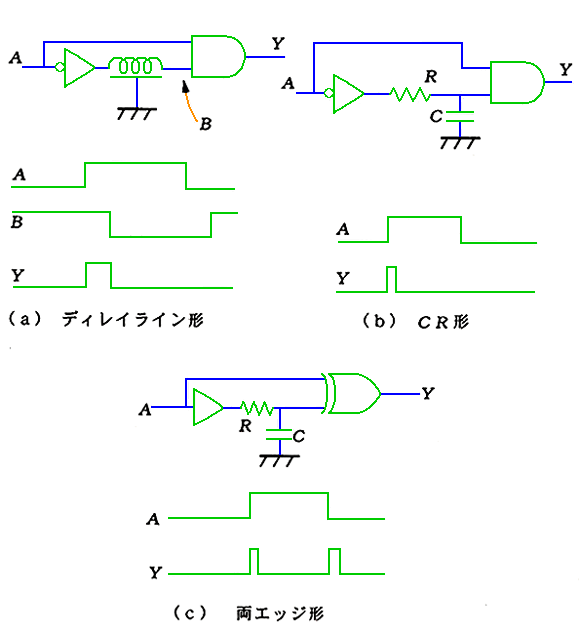
信号遅延回路は、遅れを発生させる回路です(図 5.2-75)。(a)のディレイライン は、遅れを発生させる専用の素子です。(b)の RC フィルタによる遅れや、(c)のゲートディレイと比較して、精度の高いディレイを作ることが、できます。
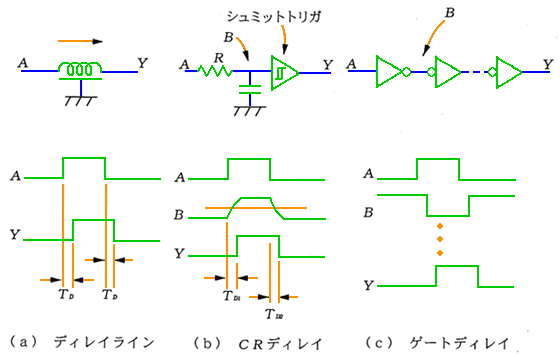
◆
イ) エッジのパルス化回路
図 5.2-76 は、信号のエッジ (立ち上がり/立下り)でパルスを作る回路です。たとえば、信号の終わりのところに、パルスを作り、そのパルスで、フリップフロップをリセットするような、場合に使用します。
★ ラッチ とは、掛け金のことです。下図左は、食器戸棚のラッチです。また、中は、窓の電動ラッチです。そして右は、耐震ラッチです。


★ 耐震ラッチは、地震に対して有効です。しかし、耐震ラッチには、規格や設置基準などがありません。どの程度信頼できるのかが、心配です。
阪神淡路大震災のときの実績では、耐震ラッチがある扉も、ほとんどは、開いていたとのことです。ということは、中身が飛出していたことになります。
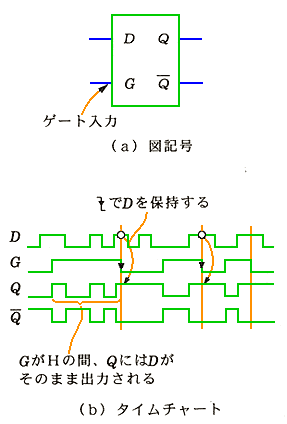
★ 電子回路には、D ラッチ と呼ばれるものがあり、フリップフロップと類似の働きをします。D ラッチは、トランスパレントラッチ ともいいます。フリップフロップと異なる点は、下図に示されているように、制御信号 G がハイのとき、D の変化が、そのまま出力されることです。
★ ラッチという言葉は、注意しないと、紛らわしい言葉です。ラッチする のように、動詞として使ったときは、クロック信号によって、あるタイミングで、値を保持する意味になります。しかし、使用する素子が、フリップフロップであるか、トランスパレントラッチであるかによって、その動作が異なります。
単に「ラッチする」という言葉は、使わないようにすべきです。ただし、世間では、「ラッチする」の言葉は、多く使われています。前後の文脈から、その意味を推定しなければ、なりません。
★ 名詞で、ラッチといったときは、フリップフロップと、トランスパレントラッチとを、総称したものと、トランスパレントラッチだけを指したものと、人と時によって異なります。フリップフロップとトランスパレントラッチとでは、動作が異なります。
★ IC の正式名称には、単なるラッチは無く、トランスパレントラッチです。このトランパレントラッチは、ラッチと略称することなく、フルネームで呼ぶか、少なくとも、D ラッチと呼ぶべきです。
★ 回路の状態を表現する方法には、各種あります。最も基本的なのは、真理値表です。真理値表は、落ちが無いものを作ることができる、という点で優れています。しかし、状態が、動的にどのように変化して行くか? ということは、よく分かりません。この意味では、状態遷移図が勝れています。
★ 状態遷移図は、直感性が高いことが特徴です。しかし、落ちがあっても、チェックが困難です。落ちをチェックすることができ、この意味で、真理値表に対応するのが、状態遷移表(下図)です。
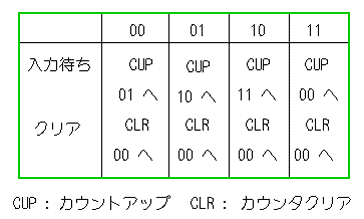
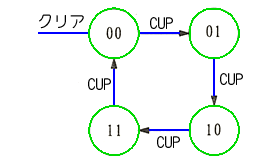
★ この状態遷移表は、クリアが入っています。このクリアが入ったものに対応する状態遷移図は、下図です。図では、○ の中に、状態が記入されているほか、線の所に、状態を変化させる操作、要因が入っています。状態遷移図は、本式には、このように書きます。しかし、簡単であり、書かなくても充分理解できるので、本文の状態遷移図では、省略してあるのです。
★ ソフトウェアでは、フローチャート が用いられます。フローチャートも、回路の状態遷移を表すのに使用できます。フローチャートは、状態遷移を表すのに、最適ではありません。しかし、フローチャートに慣れた技術者には、分かりやすいでしょう。
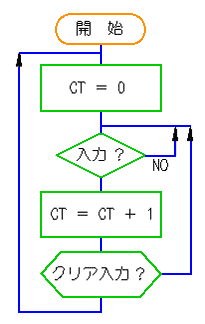
★ ソフトウェアは、命令を実行し続けます。ある状態にとどまることはありません。フローチャートは、このような仕事を表現するのに適しています。これに対して、ハードウェア(順序回路)は、ある仕事をすると、次の仕事を行うための、待機状態になり、次の仕事を開始するトリガで、次の仕事に入ります。状態遷移図は、このような仕事を表すのに適しています。
フローチャートでは、待機状態を表すのに、ループをを使用します。
★ 同期式と非同期式とを比べたとき、同期式の方が、ノイズに強いと言われています。これは、事実です。しかし、その理由として、一般に言われていることは、正しくありません。従来の説は、下記のとおりです。
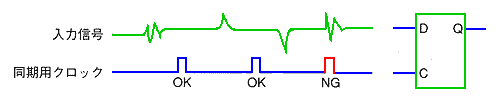
★ 同期式では、入力信号にノイズが載っていても、ノイズのタイミングが、クロックのタイミングと一致しなければ、誤動作になりません。たまたま、クロックのタイミングと一致したノイズだけが、誤動作に繋がります。だから、ノイズに強いと言う説です。
これは、真っ赤な うそ ではありません。しかし、この現象は、同期式固有の現象ではなく、非同期式でも発生します。ですから、同期式が、非同期式よりも強いという、要因には、なりません。
★ 本当の要因は、下記と、考えられます。
一般にノイズは、回路の外部から入ってくると思われています。しかし、それだけではありません。入力信号や出力信号は、自分自身が、ノイズ要因になり、他に影響します。
非同期式では、クロック、またはそれによる出力信号の変化のタイミングは、ランダムです。互いにノイズになる可能性があります。
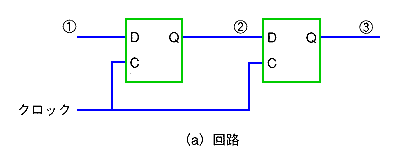
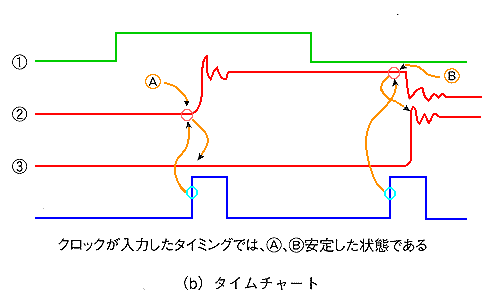
★ これに対して、同期式では、下図に示すように、クロックによって発生する、各種の信号の変化は、必ずクロックが入力した後です。次のクロックが入力する以前に安定します。したがって、同期式では、クロックが入力するタイミングでは、自分自身による、ノイズの影響が、ありません。
★ 世の中は、進歩し続けています。何をもって進歩というか については、異論があるところで、見方によっては、退歩となるものもあるでしょう。
この問題は、さて置くとして、いろいろなものが、増加していることは、事実です。下図は、エネルギー消費量の変化です。
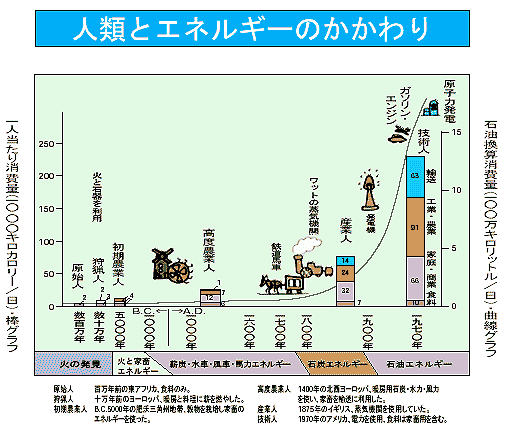
★ エネルギーの消費は、増加しつづけていますが、1800 年を境にして、その増加速度が、大きくなっていることが、分かります。ワットの蒸気機関の発明によって、動力を使用するように、なったからです。これが、産業革命です。
★ この産業革命 のような、節目を境にして、時代を区切ることが、できます。図においても、「火の発見」、「火と家畜エネルギー」、「薪炭・水車・風車・馬力エネルギー」に、時代を分けています。産業革命後も、エネルギー源によって、「石炭エネルギー」、「石油エネルギー」に分けています。
★ 産業革命は、別の見方をすることも、できます。産業革命の、前と後とで、変化の速度が異なっていることです。図は、エネルギー消費量ですが、その他、いろいろな意味で、変化が速くなっています。
★ さらに、もう一つ、別の見方をすると、産業革命は、生産における革命だと言うことです。下図では、この産業革命を、第 1 次(産業革命)と、呼んでいます。
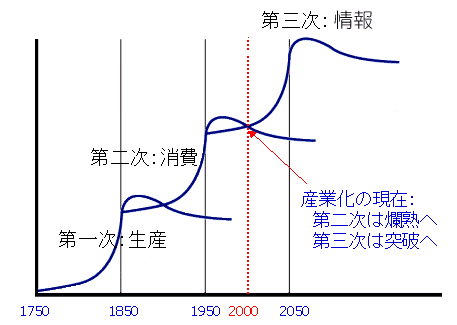
★ そして、第 2 次の産業革命が、消費における産業革命です。現在は、この第 2 次産業革命の爛熟期にあると、考えられます。さらに、次の産業革命が、第 3 次産業革命で、それは、情報(IT )における、産業革命です。IT 革命と呼ばれており、今や、IT 革命に突入し始めています。
★ 情報の革命ですから、この意味では、無形です。しかし、この IT 革命は、ハードウェアに、裏打ちされています。コンピュータをはじめとする情報機器です。コンピュータは、電子機器であり、電子機器は、電子回路で構成されています。
★ さて、前置が長くなりましたが、電子回路を構成する部品の、主要なものは、集積回路です。集積回路の集積度は、年を追って、どんどん高くなっています。この、集積度の増加速度を予測したのが、ムーアの法則です。この、ムーアの法則は、1965 年、まだ集積回路の規模が、50 トランジスタ程度だっだときに、発表されたものです。
★ ただし、法則と呼んでいますが、法則の定義に従った内容では、ありません(法則の定義は、コラム 2.1-4 参照)。あくまでも、予測です。
ムーア氏(インテル社)の論文によれば、「これまで、半導体の集積度は、1 年で、ほぼ、2 倍の割合で増加してきた。今後も、しばらくは、このペースを、期待できる」というものです。これを、ムーアの法則 といいます。下図は、その論文中の図です。
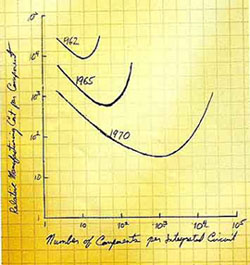
★ その後 5 年ほどは、予想通りに推移しました。
しかし、その後、集積度の増加割合は、鈍化しました。このため、ムーア氏は、1975 年に、「2 年で 2 倍」と改めました。
ムーアの法則として、一般には、18 ヶ月で 2 倍という値が使われています。この値の出所は、不明です。ムーア氏が言ったのでは、無さそうです。
★ ムーアの法則は、ここ当分の間、成立すると、考えられています。しかし、10 年ほどで、限界がきます。ムーアの法則が、成り立つのは、集積回路の、微細化 が寄与するからです。回路を微細化すれば、同じ面積のチップに、多くの回路を集積することが、できます。その微細化が、限界に達します。
★ もう一つの要因が、リーク電流です。リーク電流 というのは、集積回路で、本来の電流の流路出ないところを、漏れて流れてしまう、電流のことです。リーク電流が大きいと、無駄な消費電流 が増大します。消費電力が増大すると、放熱を、十分に行わないと、素子の温度が上昇します。この点からの、限界が生じます。