◆ 以上説明したことによって、圧縮した論理、したがって、無駄の無い回路を構成することができます。しかし、共通項を見つけるのに、勘や経験が必要です。この点を改良したものに、カルノー図があります。
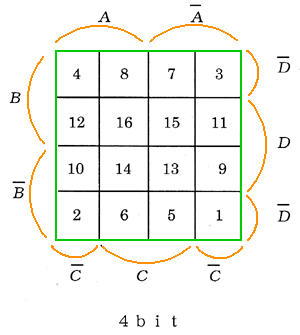
まず、カルノー図 の作り方を説明します(図 5.2-53)。
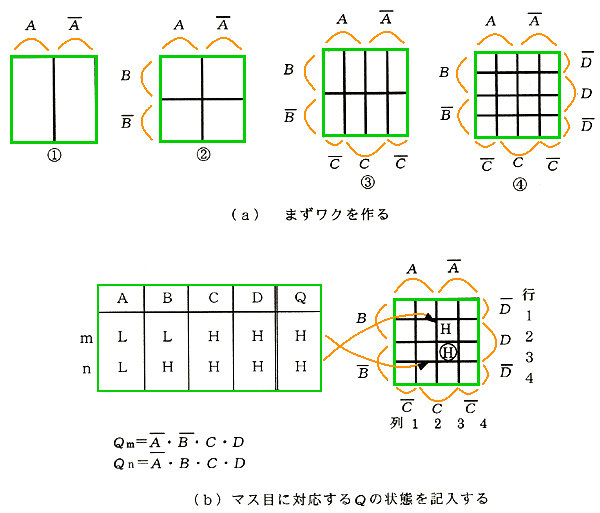
◆ (1) 外枠を作り、それを左右(または上下)に 2 分して、一方を A に、他方を A に割り当てます(図の(1))。
(2) さらに、上下(または左右)に 2 分し、一方を B に、残りを B に割り当てます。以上で、2 ビットのカルノー図が、できました(図の(2))。
(3) A と Aの領域を、それぞれ 2 分して、内側の 2 個所を C に割り当て、両端を C に割り当てれば、3 ビットのカルノー図ができます(図の(3))。
(4) さらに、B と B の領域を、それぞれ上下に 2 分して、内側の 2 個所を D に割り当て、残りを Dに割り当てれば、4 ビットのカルノー図になります(図の(4))。
◆ 次に、枠の桝目に、出力 Q の値(H/L)を記入します(図の(b))。
第 m 項の Q がハイとなる条件は、
A = L、 B = L、 C = H、 D = H
が同時に成り立つことです。
これに対応する桝目は、A、B、C、D の領域が、全て重なり合う部分、すなわち、3 行 3 列目です。ここに H を書き込みます。
◆ 同様にして、 n 項は、2 行 3 列目に対応しますから、そこにも H を書き込みます。
このようにして、真理値表の Q の値を、全てカルノー図に移しかえます。
もし、使用しない項があれば、その部分には、× を記入しておきます。これは、後に、H/L のいずれか都合の良い方に書きかえることができます。
カルノー図は、H だけでなく、L も記入して差し支えありません。しかし、H だけを書き込んだ方が、見やすいです。
◆ できあがった、カルノー図から、論理式 を作ったり、直接論理図を書いたりすることもできます(図 5.2-54)。
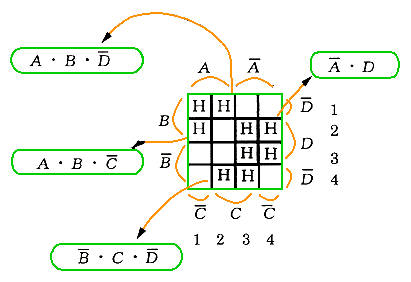
◆ (a) A と D の領域が、重なった部分を見ると、H で桝目が埋め尽くされています。したがって、この 1 かたまりを、1 つの項として表現することができ、「A ・ D 」となります。
(b) 4 行目は、2 つの H がかたまっており、その属する領域は、「B ・ C ・ D」です。
(c) 1 行目と 1 列目のところには、3 個の H が並んでいます。この部分を、うまく工夫してまとめると、論理圧縮の程度を、高くすることができます。角の H を重複させて、横並びの 2 つの H と、縦並びの 2 つの H との、2 グループを作ります。横並びの 2 つを領域「A ・ B ・ D」とし、縦並びの 2 つは領域「A ・ B ・ C」に属させます。
◆ 以上の OR をとれば、Q は、
Q = A ・ B ・ C + A ・ B ・ D + B・ C ・ D + A ・ D
のように、論理圧縮することができます。
◆ なお、完成した論理式から、逆に真理値表を作って確認するという作業を行って、チェックします。カルノー図から、直接回路設計を行っても、差し支えありませんが、この場合も、チェックが必要です。
◆ カルノー図によって回路設計を行うとき、グループ分けの、やり方によって、論理圧縮に、上手下手ができます。グループ分けを、次のようにすると、良いでしょう。
(ア) グループの数は、少ない方が良い。
(イ) 重複があっても差し支えありませんから、できるだけグループの大きさを、大きくします。
◆ 例題として、ワンインクリメント アダーを、設計してみましょう。ワンインクリメント アダー とは、与えられた入力(2 進数)に対して、それに 1 を加えた数が出力されるアダーのことです。真理値表は、図 5.2-55 です。
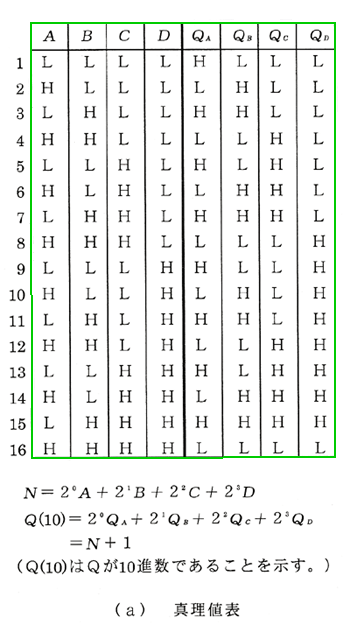
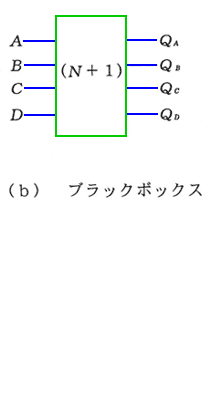
◆ 出力は、QA〜QD の 4 ビットです。その、それぞれについて、カルノー図を作ります(図 5.2-56)。なお、真理値表との対応を、図 5.2-57 に示しておきます。
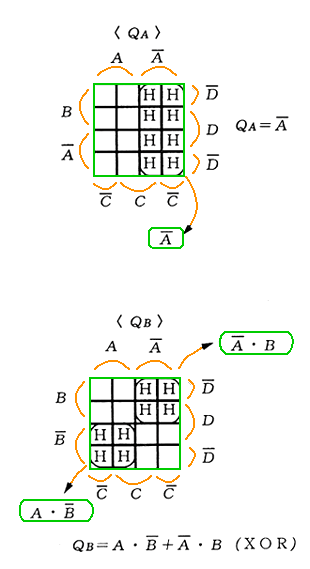
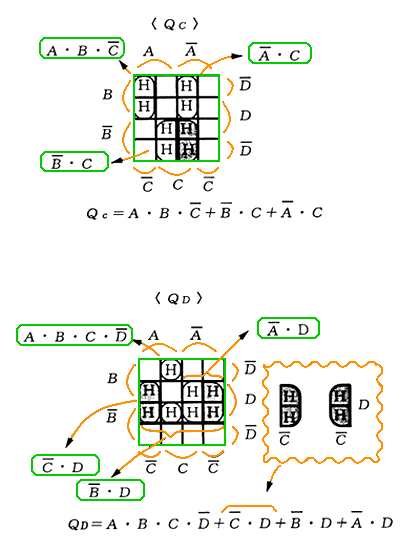
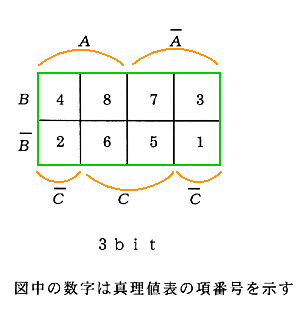
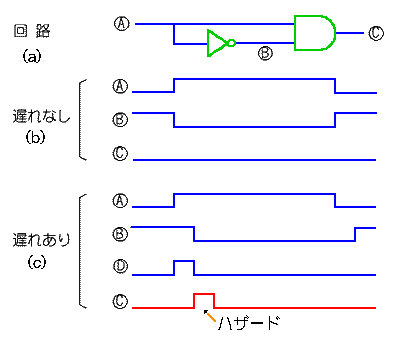
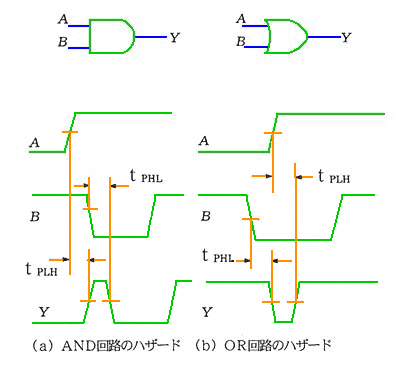
◆ ディジタル IC には、遅れがあります。この遅れによって、ゲート出力に、論理上は発生しないはずのパルスが、発生することがあります。これを、ハザード (通称 ヒゲ )といいます(図 5.2-58)。詳しくは、AND のときと、OR のときとでは異なり、図 5.2-59 のようになります。
◆
図 5.2-58 の回路で、もし素子に遅れが無ければ、(b)のようになりますから、何も問題は起こりません。しかし、実際には、遅れがあリますから、(c)のようになって、ハザードが発生します。
ハザードが発生しても、差し支えない回路もありますが、回路によっては、重大な誤動作になります。
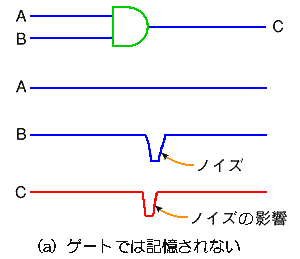
◆ とくに、フリップフロップの場合には、問題になります。フリップフロップでは、一時的なハザードが、フリップフロップの記憶機能によって、長時間の誤動作になり得るからです(図 5.2-60)。
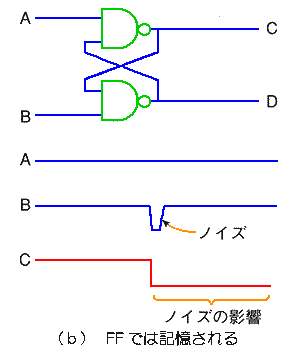
◆ 図 5.2-58 は、ハザード発生の機構を説明するための、模型的な図です。実際には、ゲート 1 段分の遅れでは、ハザードは、発生するときと、発生しないときとがあります。しかし、遅れが 2 段分になると、ハザードは、確実に発生します。
◆ ハザードが発生する可能性がある場合には、ハザード対策回路 によって、ハザードを防止します。データセレクタ回路を例にとって説明します(図 5.2-61)。データセレクタ は、複数の入力から、特定の 1 つを選択して出力する回路です。図では、A、B の 2 入力から、セレクト入力 S によって、その一方を選択し出力します。
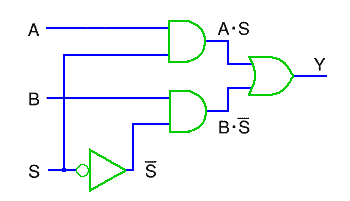
◆ この図の回路では、切り替え時に、ハザードが発生します。図 5.2-62、図 5.2-63 は、ハザード対策を施した回路です。
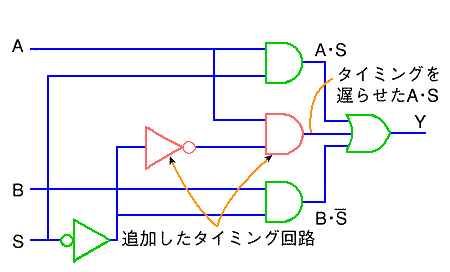

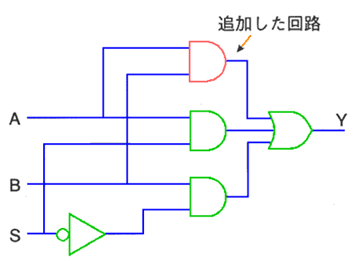

◆ いずれも、論理は、元のままで、タイミングだけを変えた回路を追加して、ハザードを消しています。
★ 圧縮 とは、押し縮めることです。空き缶は、そのままでは、かさばりますから、圧縮して、容積を減らして運びます。布団も収納にかさばりますから、圧縮袋で圧縮して、保管します。


★ 略語も一種の圧縮です。うなどん などは、昔からある略語です。最近は、カーナビなど、横文字略語の全盛です。


★ さて、データ圧縮 は、一定の手順にしたがって、データの意味を保ったまま、容量を削減する処理のことです。逆に、圧縮されたデータを元のデータに復元する処理は「解凍 」とか「展開 」「伸張 」「減圧 」「抽出 」などといいます。

★ ここでいう、データ圧縮のデータは、一般には、画像データ や文字データ など、のことです。
次に、圧縮と解凍の手順を示します。データ圧縮は、データ伝送量を減らしたり、データの保存量を少なくするのに、有効です。
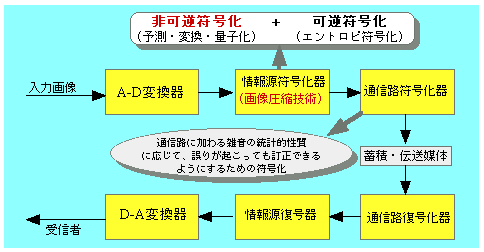
★ 簡単なデータ圧縮の例として、FAX (ファクシミリ ) の例を示します。

★ FAX では、2 次元の画像データを、多数の方眼状の点で表します。この 1 つ 1 つの点を、画素 (ピクセル )といいます。
★ この、画像データを、スキャン(走査 )して、1 次元の直列データ に変換して送り、受信側で、これを 2 次元データに復元します。
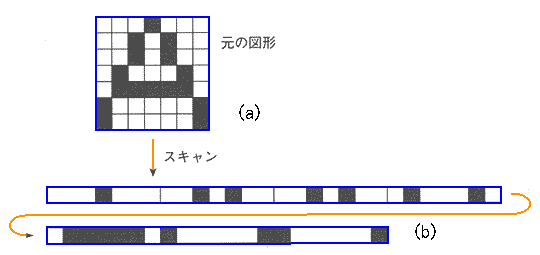
★ このとき、0/1 のデータを、まともに送らないで、データ圧縮します。FAX のデータ圧縮の方法は、単純です。
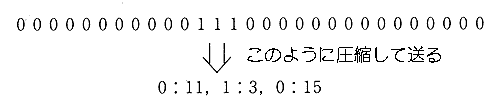
★ 簡単な圧縮の、もう 1 つの例を、示します。音声は、アナログですが、音声信号は、ディジタル化し、圧縮して送ることが、多いのです。ISDN というシステムも、その 1 つです。
★ 人の耳の特性は、非線形です。小さな音は、細かな差を聞き分けることができますが、大きな音では、細かな差は分かりません。音声を、ディジタル化するときは、人の耳の特性に合わせて、圧縮します。
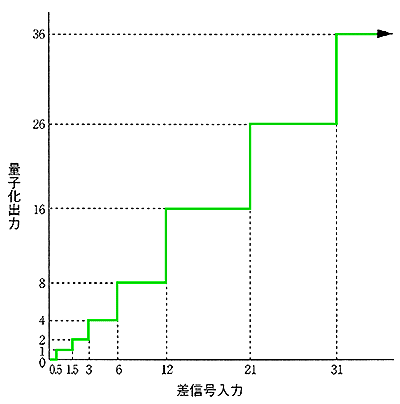
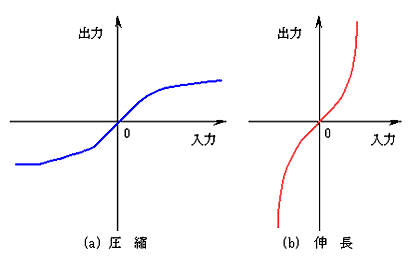
★ 以上、圧縮を、ディジタル信号の圧縮として、説明しました。アナログ信号にも、圧縮/伸張があります。広いダイナミックレンジを持つアナログ信号を、伝送するとき、このアナログ信号を、圧縮して送り、受信側で、元の信号に、伸張します。
★ ダイナミックレンジ とは、信号の再現能力を表わす数値で、信号の最小値と最大値の比のことです。ダイナミックレンジは、dB(デシベル)で表わします。