

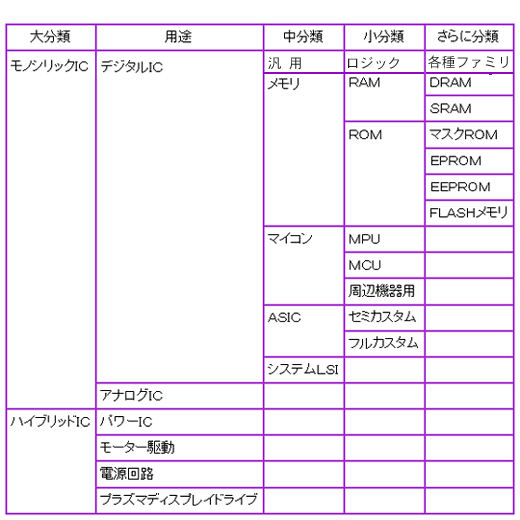
◆ 現在私たちが使っている半導体素子は、数の上からは、圧倒的に多くが、ディジタル ICに分類されます(図 5.1-1)。図で、モノリシック IC とは、1 チップで構成された IC (集積回路)のことです。ハイブリッド IC は、1 枚の基板上に、IC チップ、抵抗、コンデンサなどを組み込んだものです。
◆ 最初に作られた IC は、ディジタル IC で、そのまた最初が、汎用ロジック IC です。ロジック IC は、論理演算(ロジック演算 )を実行する IC です。
◆ 私達が、日常使っている、最も普通の演算 は、算術演算 です。算術演算は、数を対象とした演算であり、算術演算の基本は、四則演算 (加減乗除、+、−、×、÷)です。
これに対して、論理演算 (ブール代数 、ブーリアン )は、数では無くて、論理 (ロジック )を対象とする演算です。論理は、真 (TRUE )と偽 (FALSE )との 2 つの論理値 を持っています。しかし、真/偽 の言葉は、いかめしいので、通常は、真を T で、偽を F で表します。または、真を 1 に、偽を 0 に対応させて表現します(図 5.1-2)。ディジタル IC では、電圧のハイ (高い)とロー (低い)で、論理値を表します。なお、論理演算は、ディジタル演算 とも、呼んでいます。
| 真 | TRUE | T | 1 | 電圧 ハイ |
| 偽 | FALSE | F | 0 | 電圧 ロー |
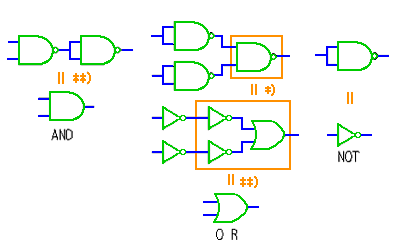
◆ 論理演算(図 5.1-3)は、AND (左上)、OR (右上)、および NOT (右下) の基本演算を持っています。すべての、論理は、この 3 つから、導くことができます。
論理演算の内容を、図に示した表のような、形式で表したものを、真理値表 といいます。真理値表は、各行において、入力 A、B の論理演算の結果が、出力になることを表します。たとえば、AND において、入力が、A = 0、B = 0 のときに、その出力が、0 になります。
◆ 論理演算の結果を、分かりやすく直感的に示したものが、○ で示した図です。ベン図 といいます。
図では、2 入力の論理演算を示しましたが、多入力も可能です(図 5.1-4)。
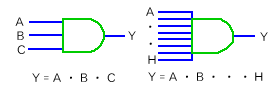
論理演算は、図 5.1-3に示したように、図記号 で表すことができます。論理演算はまた、式の形でも、表わすことができます。A と B との演算結果を C とすれば、
AND : C = A ・ B
OR : C = A + B
です。また、NOT は、入力の上に、 を付けて表します。プリントの都合で、 を使うことができないときは、/ で代用します。
NOT : C または、 /C
です。
◆ エクスクルーシブ OR (図の EOR ) は、AND、OR、NOT から論理演算によって作ることが可能です。エクスクルーシブ OR の演算記号を、![]() とすれば
とすれば
A ![]() B = A ・ B + A ・ B
B = A ・ B + A ・ B
です。したがって、エクスクルーシブオアは、基本演算ではありません。しかし、エクスクルーシブオアは、頻繁に使いますから、通常は、基本演算と同列に取り扱っています。EOR は、XOR とも書きます。
◆ 論理演算記号の書式は、この他にも、各種あります。算術演算記号と同様な記号が、分かり易いので、それを示しました。
◆ 論理演算の基本法則を、図 5.1-5 に示します。なお、算術演算と同様に、・ (AND)は、+ (OR)に優先します。たとえば、A + B ・ C は、A + (B ・ C) です。

◆
図で、* 印は定理、その他は法則です。
ド・モルガンの定理 は、NOT することによって、AND は OR に、OR は AND に変換されることを、示しています。
AND と NOT を組み合わせたものを、NAND 、OR と NOT を組み合わせたものを NOR といいます(図 5.1-6)。

◆ NAND は、NAND だけを複数組み合わせることによって、全ての論理を作ることができます(図 5.1-7)。AND、OR、および NOT の基本演算から、全ての論理を作ることができます。したがって、NAND から、AND、OR、NOT を作ることができれば、このことが、成立します。図で、*) のところは、ド・モルガンの定理の(2)による変形です。また、**)は、ド・モルガンの定理の(i)による変形です。
[図 5.1-7] NAND から、AND、OR、NOT を作る
◆ 図 5.1-3 に示した、0 と 1 とは、実は、私達が、日常使っている、数字ではありません。2 進数と呼ばれるものです。私達は、10 進数 の世界に住んでいます。時間などの、僅かの例外を除いて、ほとんどの数は、10 進法 です。私達が、10 進法を使うようになったのは、手の指が、5 本(両手で 10 本)だったからです。
数学的には、10 という数は、あまり優れた数では、ありません(コラム 5.1-2)。電子回路や、コンピュータなどでは、10 進数よりも、2 進数で取り扱う方が、便利です。
◆ 2 進数 (2 進法 )は、0 と 1 の 2 つの数字だけからなる、数の体系です(図 5.1-8)。2 進数では、0、1、の上は、桁上がりします。10 進法の 2 は、2 進数では、10 になります。
2 進数の 1 桁のことを、1 ビット (BIT )といいます。図は、4 ビットの数です。10 進数の 1 桁は、1ディジット (DIGIT )といいます。
|
|
◆ 2 進数は、人間にとっては、桁数ばかり大きくて、分かり難い体系です(進数は、コラム 5.1-2 参照)。しかし、電子回路や、コンピュータにとっては、2 進数の方が、都合がよいのです。しかし、この辺のお話は、後に回し、論理の、お話に戻ります。
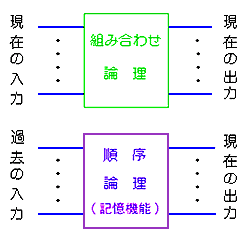
◆ 論理は、いままで、お話ししてきた、論理の他に、もう一つ別の論理が、あります。これを、順序論理といいます。順序論理 とは、過去の状態が、現在の出力に影響する論理です。すなわち、現在の出力が、現在の入力だけからは、決まらない論理です。過去の状態が、現在に影響を及ぼすためには、過去の状態を記憶していなければ、なりません。順序論理は、記憶機能 です。この順序論理に対して、いままで、お話してきた論理のことを、組み合わせ論理 といいます(図 5.1-9)。
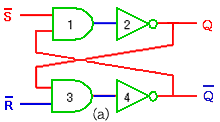
◆ 順序論理は、フリップフロップ (FF , 以下、フリップフロップを FF と書きます)と呼ばれる回路によって、組み合わせ論理から、作ることができます(図 5.1-10)。図は、NANDから作った、最も基本的な FF で、RS FF(RS フリップフロップ 、セットリセットフリップフロップ )といいます。図は、フリップフロップの、初期状態です。見やすいように、赤で 1(ハイ)を、青で 0(ロー)を表しています。入力は、2 つで、S をセット入力 、R をリセット入力 といいます。
◆ この FF は、入力がハイのときが、初期状態で、入力がローになることによって、動作します。入力に NOT を意味するバーがついているのは、このことを、示しています。素子の出力が、動作状態にあることをアクティブ 、動作状態に入れることをアクティブにするといいます。逆に、アクティブでないのが、非アクティブ です。
FF の出力は、通常 2 つが組になっています。ちょうどシーソーのように、一方がハイのとき、他方はローとなります。FF の 2 つの出力は、通常、Q と Q で表します。S 入力に対応する出力が Q で、R 入力に対応する出力が Q です。
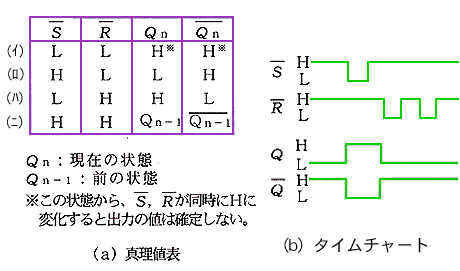
RS フリップフロップの真理値表を、図 5.1-11 に示します。この真理値表の入力は S、R の列、出力は Qn、Qn の列です。真理値表は、図 5.1-3のように、入力/出力の文字を記載すべきですが、この例のように、省略することが多いようです。このことは、FF の真理値表だけでなく、全ての真理値表について、言えることです。
[図 5.1-11] RS フリップフロップの真理値表とタイムチャート
◆ 図には、タイムチャートも載せてあります。タイムチャート とは、信号の、時間的な変化の様子を示す図です。タイムチャートは、横軸が時間で、縦軸が信号です。
以下、RS フリップフロップの動作を説明します。
(1) 初期状態(図 5.1-10)は、真理値表(図 5.1-11)では、(ニ)です。真理理表の、出力 Qn-1、Qn-1は、初期状態を意味します。このフリップフロップでは、入力の初期状態は、H(ハイ)です。
(2) 入力 S をL(ロー、アクティブ)にします(図 5.1-12)。
◆ 出力に、変化はありません。図5.1-11 の S をハイに戻せば、初期状態(図5.1-10)に戻ります。初期状態に戻っても、出力(Q、Q)の値は同じです。
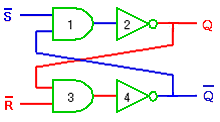
(3)次に、初期状態(図5.1-10)から、入力 R を、ロー(アクティブ)にします(図 5.1.13)。図の(a)を経て、図の(b)になります。
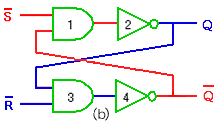
◆ この図の(b)の状態は、図 5.1-11 の(ロ)の状態です。Qn がロー(アクティブ)になっています。入力 R をハイに戻しても、出力は変化しません。
以上から、RS FF では、入力 S をアクティブ(ロー)にすれば、出力 Q がハイ(アクティブ)に、出力 Q がロー(非アクティブ)になります。この操作を、セット するといい、セットされた結果の状態を、セット状態といいます。
入力 R をアクティブ(ロー)にすれば、出力 Q がロー(非アクティブ)に、出力 Q がハイ(アクティブ)になります。この操作を、リセット するといい、リセットされた結果の状態を、りセット状態といいます。
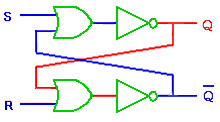
◆ 以上、NAND を使用した RS FF について、説明しましたが、NOR を使用しても、RS FF を作ることができます(図 5.1-14)。NOR による RS FF の入力の初期状態は、ハイ(H)です。
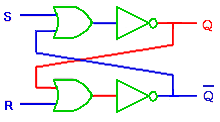
◆ FF は、RS FF 以外にも、各種ありますが、RS FF が基本です。他の種類の FF も、RS FF から作ることができます。
_