

◆ 論理は、真理値表の形で与えられるのが、最も落ちが無い表現法です。真理値表は、落ちがあれば、そこは空欄です。空欄を無くせば、落ちは無くなります。この意味で、まず真理値表を作り、その真理値表を充分にチェックしてから、その真理値表をから、その論理を実現する、回路設計を行うことが、最も確実な手順です。
◆ 真理値表を元にして、回路設計を行う、汎用的な設計法を説明します。ここでは、正論理の場合について、述べますが、負論理も、同様な方法で、設計することが、できます。
全ての論理は、標準積和形 という、形式にまとめることができます。標準積和形は、ゲートの段数が、3 段以内に収まるという点でも、優れています。ゲートの段数が多いと、ゲートによる遅れが大きくなります。
◆ 標準積和形を、具体例で説明します。真理値表が、図 5.2-41に、与えられたとします。
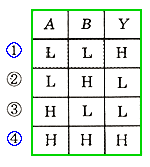
◆ 真理値表(図)で、出力がハイ(H)になっている行に注目します((1)と(4))。この(1)と(4)のいずれかが(OR)のとき、出力がハイになるのですから、この、(1)と(4)との OR が、例題の解に、なります(図 5.2-42)。
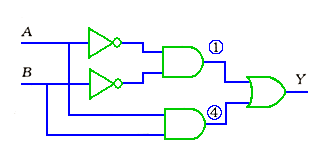
◆ これは、第 1 段で、入力の AND (論理積 )を取って、第 2 段で、第 1 段の OR (論理和 )を取っています。このことから、標準積和形の名が付いたのです。
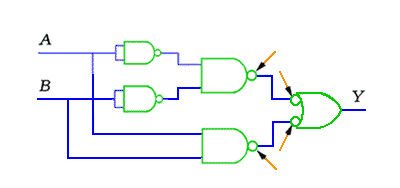
ただし、この解では、回路は得られますが、現実の IC に即した回路ではありません。したがって、これを変形します。NAND の IC を使用したときの例を、図 5.2-43 に示します。図の、矢印の部分は、図 5.2-40 に示した、変形です。
◆ [例題 2] 図 5.2-44 は、エクスクルーシブオア(EOR)の真理値表です。EOR は、IC がありますから、作る必要はありませんが、練習です。
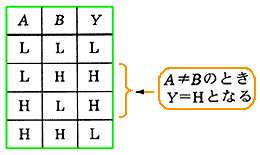
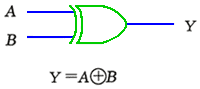
◆ EOR を、標準積和形で、作って見ましょう(図 5.2-45)。出力が、ハイになるのは、(2)と(3)ですから、その OR を取ります。
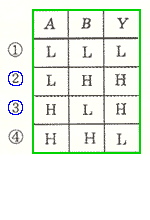
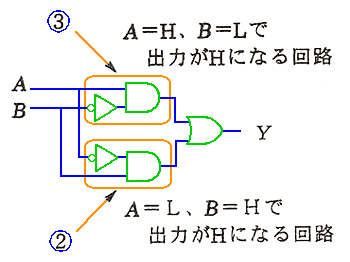
◆ 論理に AND と OR とがあるように、標準積和形に対応して、標準和積形 も、存在します。図 5.2-46は、EOR を標準和積形で作ったものです。
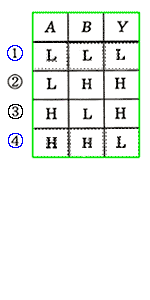
◆ 標準積和形(または、標準和積形)によって、全ての論理を回路化することができます。しかし、これによって得られた結果は、必ずしも、最適な回路では、ありません。冗長な、回路を含む場合があります。エクスクルーシブオアは、単純なので、無駄の含みようが、無かったのです。
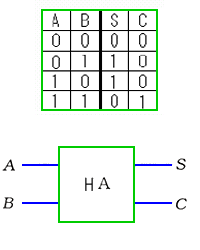
◆ この例題は、2 進数のアダー (加算器 )です。加算においては、桁上がり があります。桁上がりの制御には、キャリ (Co)と呼ばれるビットを使用します。キャリビットを使用して、下位からの桁上がりを受け入れ、自身に桁上がりがあるときは、キャリビットによって、上位に桁上がりがあることを通知します。このやり方が、本式のアダーです。この本式のアダーのことを、フルアダー といいます。これに対して、ハーフアダー は、キャリビットを立てますが、下位からの桁上がりは、受け付けません。
アダーの真理値表を、図 5.2-47 に示します(FA : フルアダー、HA : ハーフアダー)。
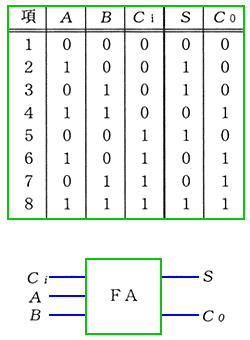
◆ フルアダーの回路を設計します。
まず、S が 1 になる項を拾い出します。第 2 項は、S が 1 です。第 2 項は、A = 1、B = 0、C = 0 です。したがって、
S2 = A・B・Ci
です( は、NOT を表します。5.1.(2-A)参照)。第 3 項は、A = 0、B = 1、C = 0 ですから、
S3 = A・B・Ci
同様にして、第 5 項および第 8 項は、それぞれ、
S5 = A・B・Ci、 S8 = A・B・Ci
です。残りの、第 1、4、6、7 項の出力は 0 です。
◆ 以上から、
S = S1 + S2 + S3 + S4 + S5 + S6 + S7 + S8
= 0 + A・B・Ci + A・B・Ci + 0 + A・ B・C + 0 + 0 + A・B・Ci
= A・B・Ci + A・B・Ci+ A・B・Ci + A・B・Ci
となります。
この論理式の、AND(式では、乗算記号 ・) を AND ゲート、OR を OR ゲートと置くことによって、論理図を作ることができます。
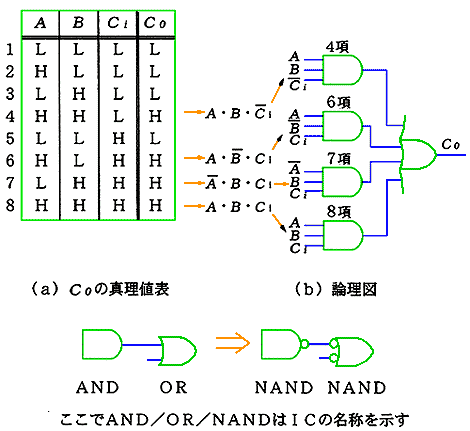
◆ キャリ(Co)についても、同様にして、回路を設計することができます(図 5.2-48)。
◆ ここで、もう一度、手順を、整理してみます。
a) 真理値表を作ります。
b) 出力がハイ(1)になっている、項に着目し、その項について、AND が成立する入力の組合せを書き出します。
c) 各項ごとに、前記入力を、AND ゲートに加えます。
d) 全ての AND ゲートの出力を、OR ゲートの入力に、加えます。
◆ 完成した、フルアダーの論理図を、図 5.2-49 に示します。
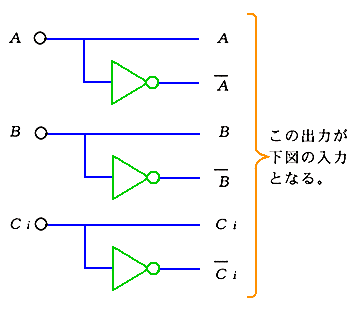
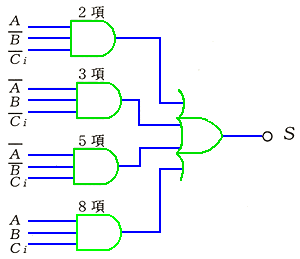
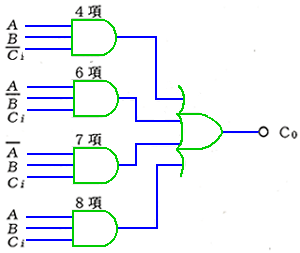
★ 標準積和形回路は、回路を、きれいにまとめることが、できます。しかし、これをロジックファミリの IC で組んだのでは、IC 数の節減、したがって、プリント基板面積の縮小には、繋がりません。
プログラマブルロジックデバイス (PLD )と呼ばれる LSI を利用することによって、真にコンパクトにまとめることが、可能です。PLD の基本構成は、次のようになっています。
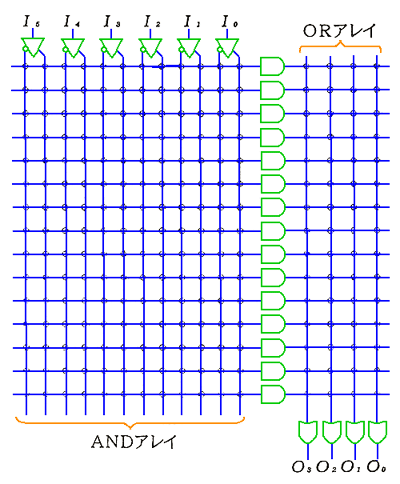
★ 図で、交点(○印)のところを、プログラムすることができます。各 AND ゲートは、プログラムによって決められた Ii および、Ii が、その入力になります。 各 OR ゲートは、プログラムによって決められた各 AND ゲートの出力が、その入力となります。その結果として、標準積和形が、形成されます。
★ PLD 製品の一例を示します。出力に、レジスタを持っている例です。また、出力を、入力にフィードバックすることが可能ですから、自由度の高い回路を組むことができます。
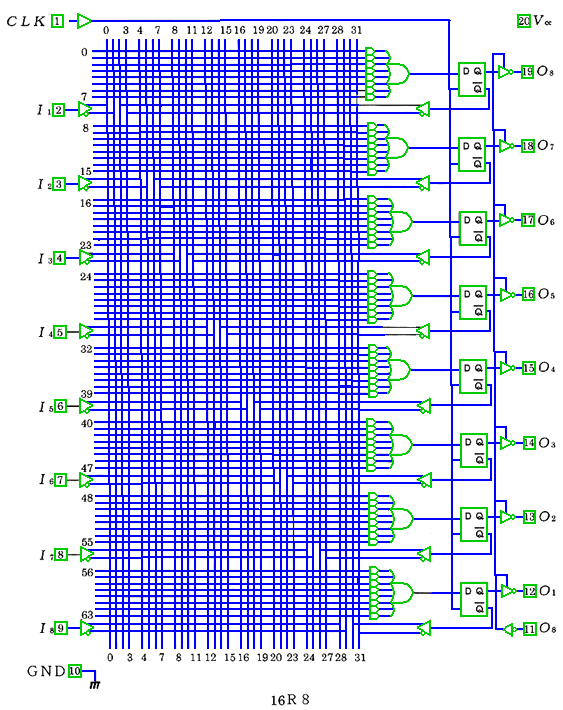
★ PLD の集積度をさらに高め、機能も強化した製品に、FPGA (フィールドプログラマブルゲートアレイ )があります。
◆ 以上の手順で、論理を作ることができます。しかし、このままでは、でき上がった論理は、回路として、余分なものが入っています。無駄(冗長)なものを取り除いて、すっきりした形に変形します。この作業を、論理圧縮 (圧縮 )といいます。
◆ ただし、論理圧縮した結果が、回路として、最適なものであるとは、限りません。現実には、多くの LSI の中から、最適なものを選ぶ方が、良いことも多いでしょう。プリント基板面積が最小である、最も安価である、などを、最適と考えることが多いと考えられます。論理圧縮しても、それで回路を組んだとき、IC の数が多くなると、意味がありません。
◆ LSI は、元々は、特定の用途に作られた、専用 LIS から出発しています。この他に、汎用的に、各種の回路を作ることができる LSI が、あります。これらの汎用的な LSI を、利用すれば、それが、最適であるかどうかは別として、ほとんどの回路を、LSI 化することができます。一般には、LSI を利用することによって、プリント基板面積を小さくすることが、できます。ただし、汎用的な LSI を利用する場合にも、論理圧縮が、役に立ちます。
◆ 図 5.1-5 で、論理演算の基本法則を示しました。この中の (o) 分配則を例題として、論理圧縮を説明します。 分配則
( A + B ) ・ ( A + C ) = A + B ・ C
は、論理圧縮になっています(図.5.2-50)。
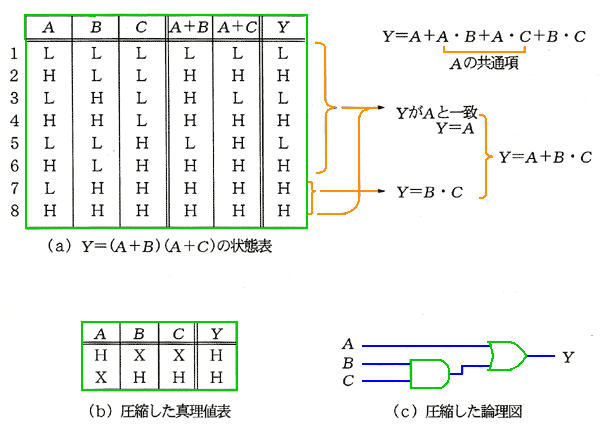
◆ 図の(a)によって、出力 Y がハイになっている項を見ると、第 7 項を除いては、Y は、A と一致していることが分かります。すなわち、第 7 項を除いては、B と C は、何の役にも立っていません。これらの、役に立っていない項のことを、共通項 といいます。
真理値表の第 7、8 項についても、B、C 項に関して、A は何の役にも立っていないことが分かります。すなわち、A は、B・C の共通項です。
以上から、図に示したように、
Y = A + B ・ C
と、圧縮できます。
◆ このようにして、真理値表の中から、共通等を外すことによって、論理圧縮することが、できます。図の(b)は圧縮した真理値表、(C)は、圧縮した論理図(回路)です。
◆ 以上、真理値表の上で考えましたが、論理式によっても、同じ結果を導くことができます。すなわち、Y = ( A + B ) ・ ( A + C ) を展開すると、
Y = ( A + B ) ・ ( A + C )
= A + A ・ B + A ・ C + B ・ C
となります。
ここで、第 2 項 A ・ B は、吸収則(q)によって、A に吸収されます。同様に、第 3 項 A ・ C も A に吸収されます。すなわち、論理式の上で、( A ・ B + A ・C )は、A の共通項です。
◆ 図 5.2-49 のフルアダーを、論理圧縮してみましょう(図 5.2-51)。フルアダーには、和とキャリとがあります。まず、和 (S)の論理圧縮を行います。
◆ S がハイになっている項に注目します。
A、B、Ci のどれか 1 つだけがハイの場合と、A、B、Ci の全てがハイの場合とがありますが、図 5.2-50 に示したような、共通項はありません。
しかし、共通項が無くても、論理圧縮が、可能なことがあります。別の方法を探して見ましょう。
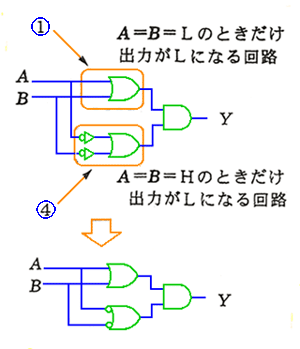
◆ 1〜4 項と、5〜8 項とは、ハイとローを反転すれば、同じ順になっていることが分かります(図の(b))。したがって、Ci がハイのとき、S を反転すれば良いわけです。Ci がハイのときだけ、入力のハイとローとを反転させることは、EOR によって実現することができます(図 5.2-46)。
◆ 以上から、図の1〜4 項を論理圧縮できれば良いことが、分かります。1〜4 項をよく見ると、これは、EOR ですから、EOR を使用すれば、それで充分です。すなわち、図の(d)となります。
◆ 次に、キャリ(Co)を圧縮します。図 5.2-52 は、キャリ(Co)の真理値表です。これは、少し見づらいので、Co がハイの項だけを記入し、ローの項を空欄にしたものが、図の(b)です。
◆ 7、8 項は、A の値に無関係に、Co の値がハイになりますから、A が B ・ Ci の共通項です。同様にして、6、8 項からと、4、8 項から、それぞれ、共通項 B と Ci とが見つかります。
以上から、4、8 項をまとめて「 A ・ B 」、同様に、6、8 項を「 A ・ Ci 」、7、8 項を「 B ・ Ci 」と表すことができ、
Co = A ・ B + B ・ Ci + Ci ・ A
が得られます(図の(c))。