◆
さて、ディジタル制御においては、サンプリングの問題が、あります。制御対象の特性に対して、サンプリング周期が長いと、サンプリングに起因する、応答の遅れが発生します。このために、制御成績が低下します。しかし、サンプリングが十分に速ければ、アナログ制御と同等の制御成績を得ることが、できます。
◆
以下のお話は、アナログ制御に関するお話ですが、サンプリングが十分に速いディジタル制御についても、適用することが、できます。
比例制御の制御演算式は、式(9.2.1) に示しました。式の定数 Kp を比例ゲイン 、定数 Km を、マニュアルリセット といいます。
◆
なお、比例ゲインの逆数を。%で表したもの、すなわち、100(1/Kp) のことを、比例帯 といい、これも、多く使用されています。
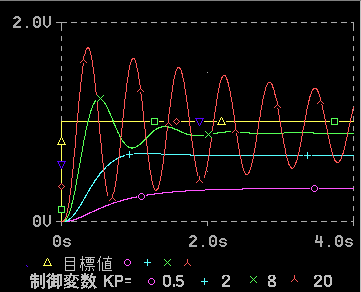
この比例ゲインの値を変えると、制御応答の波形が変化します(図 9.2-344)。
◆
図から分かるように、比例ゲイン Kp の値を大きくして行くと、2 つの現象があります。第 1 は、オフセットの値が、減少することです(図の ○ → + → ×)。これは、望ましい現象です。しかし、その代わりに、応答が振動的になります(図の× → ∧)。
この両者の兼ね合いから、最適な、比例ゲイン Kp の値が存在することが、予想されます(コラム 9.2-21 参照)。図の場合には、緑色(×)の波形が、多分最適でしょう。
◆
比例ゲインの値を、緑色よりも、さらに大きくすると、オフセットは、ゼロに近付きます。しかし、振動的になり過ぎて、実用になりません。
制御応答の波形は、比例ゲインの大きさと、制御対象の特性の、両方によって、変わります。定性的には、上記の性質は、制御対象の特性には、依存しませんが、定量的には、制御対象によって、異なります。
◆
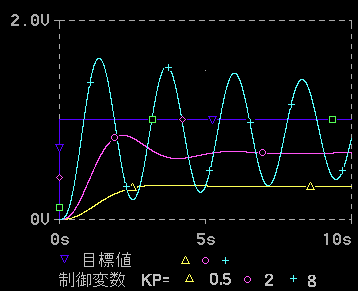
あまり振動的になり過ぎない範囲で、オフセットを実用上無視できる大きさにすることが、望ましいわけです。しかし、そのように、できるか、どうかは、制御対象の特性に、依ります。図 9.2-345 は、図 9.2-344 とは異なった特性を有する制御対象を、制御した例です。制御対象の特性の違いによる、制御応答の差が、大きいことが、分かります。
◆
図 9.2-345 の水色(+)と、図 9.2-344 の緑色(×)は、共に、比例ゲイン Kp = 8 ですが、図 9.2-344 は、適正な応答であるのに対して、図 9.2-345 では、振動的になり過ぎています。
◆
自動制御は、分かり難いと言われています。その理由の一つが、この例のように、制御応答が、制御対象の特性と、コントローラの特性との、両方に依存していて、どちららか一方だけでは、決まらないことです。
◆
マニュアルリセットは、コントローラを手動でリセットします。
リセット というのは、機械装置を、初期状態に戻す作業です。たとえば、パソコンには、リセットボタンが付いています(図 9.2-25 左側 本体の中央にある黒いボタン)。何らかの理由によって、パソコンがハングアップしたときに、パソコンのリセットボタンを押して、パソコンを、リセットすれば、パソコンを、正常な状態に、戻すことが、できます。
だだし、実行中のプログラムは、ご破算になります。この意味では、リセットは、両刃の剣です。
◆
コントローラのマニュアルリセットは、パソコンのリセットとは、若干意味が異なります。しかし、コントローラのマニュアルリセットも、一種の、初期化動作です。
コントローラのリセット、すなわち初期化は、外乱が無い状態で、偏差をゼロにする操作です。
◆
比例制御では、コントローラを起動したとき、単に起動しただけでは、リセット状態にはなりません。手動でコントローラを調整して、正常な初期状態に、してやる必要があります。この調整を行うためのパラメータが、式(9.2.1)のマニュアルリセット Kmです(図 9.2-346)。
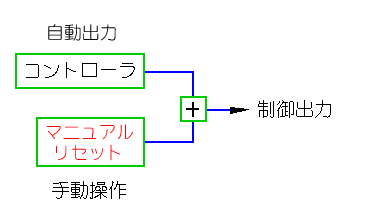
◆
図のコントローラは、コントローラ全体ではなく、自動で動作する部分を、示しています。図の手動操作 が、マニュアルリセットの操作です。
予め、偏差がゼロになるように、手動操作で、マニュアルリセットを調整しておきます。この調整は、外乱が入っていない状態のときに、行います。
◆
その上で、コントローラをスタートさせて、自動に入れます。この手動から自動に切り替えるとき、コントローラが、調節計と呼ばれる機種の場合には、切り替えがスムーズに行われるような、機構が付いています。この機構のことを、バンプレス といいます。バンプレスであれば、単に切り替えスイッチを操作するだけで、スムーズな切り替えが、できます。
◆
外乱には、一時的な外乱と、定常的に持続する外乱との、2 種類が、あります(図 9.2-347)。
◆
一時的外乱は、発生しても、そのまま放置しておいて、差し支えありません。外乱が無くなれば、偏差はゼロに戻ります。
持続的外乱 の場合には、放置すれば、それが、オフセットになります。持続的外乱が発生したときは、マニュアルリセットを用いて、その外乱を打ち消して、オフセットを無くします。
◆
しかし、持続的外乱が、頻繁に発生する制御対象では、この作業は、面倒です。
◆
前記の持続的外乱の問題を、解決するのが、オートマチックリセット (積分動作 、I 動作 )です。オートマチックリセットは、コントローラのリセット動作を、自動的に実行してくれます。オートマチックリセットの制御演算式は、積分 です(下式)。
y = Ki ∫e dt ・ ・ ・ (9.2.2)’’
ここで、y は出力、e は偏差、Ki は、定数です。Ki は、時間の逆数の次元を持っています。この Ki の逆数である、時間の次元を持つ定数 Ti = 1/ Ki を積分時間 といいます。通常は、積分時間 Ti の方を、使用します。積分時間 Ti は、短いほど、積分の効きが強くなります。
y = (1/ Ti)∫e dt ・ ・ ・ (9.2.2)’
◆
自動制御では、制御演算式を、時間関数よりも、伝達関数の形で表す方が、便利です。伝達関数を使用すれば、積分動作は、
Y = 1/(Ti s) ・ E ・ ・ ・ (9.2.2)
となります。ここで、s は、ラプラス変換子です。時間領域の変数を、f(t)、ラプラス変換領域の変数を F(s) の形で、表しています。
◆
積分動作の特性を、図 9.2-348 に示します。図の上側はステップ応答、図の中央は周波数応答です。
◆
図の下側は、積分動作の、偏差と制御出力との関係を、示したものです。
積分動作のステップ応答からも分かるように、積分動作では、偏差が存在する限り、出力は変化し続けます。偏差がゼロになると、出力は、その直前の値を、保持します(図の下側)。
積分動作において、偏差が存在する限り、出力が変化し続けるということは、オフセットを無くす効果が、あるということです。
◆
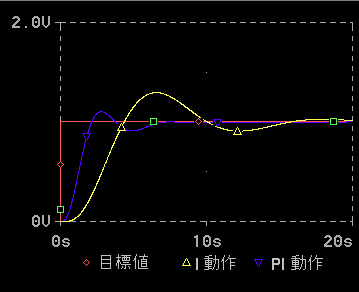
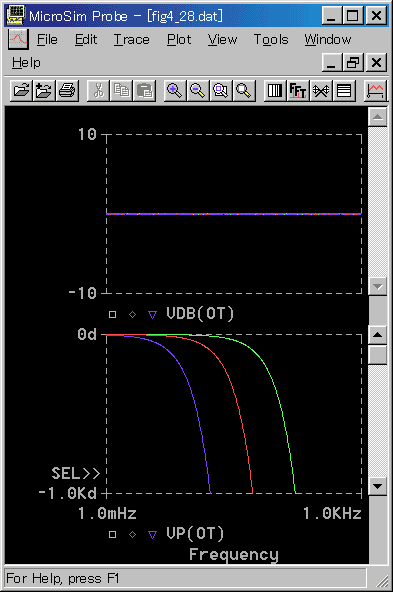
図 9.2-349 の△(黄色)は、ある制御対象を、積分動作で制御したときの、制御応答です。この制御対象は、図 9.2-344の比例制御の制御対象と同じものです。
◆
積分動作は、オフセットを無くすという、大きな効果がありますが、応答が遅いという、欠点が あります。
積分動作の、オフセットをゼロにするという機能を活かし、積分動作の応答が遅いという欠点を無くす方法として、積分動作と、比例動作とを組み合わせた、PI 動作 (比例+積分動作 )があります(図 9.2-349 参照)。
◆
PI 動作の制御演算式は、時間領域の式が (9.2.3)、 ラプラス変換領域の式が (9.2.3)’です。
Kp (e + (1/ Ti) ・∫e dt) ・ ・ ・ (9.2.3)
Kp (1 + 1/ (Ti s)) ・ ・ ・ (9.2.3)’
◆
PI 動作の制御パラメータは、Kp と Ti の 2 です。制御パラメータ とは、制御演算式における、可変の(調整可能な)定数のことです。コントローラを使用するときは、この制御パラメータの値を調整して、望ましい制御応答波形を、作り出します。
◆
PI 動作の特性は、図 9.2-350 の通りです。図の上側はステップ応答、下側は周波数応答です。図から分かるように、入力のステップ状の変化に対して、出力は、まず比例動作による分だけステップ状に変化し、引き続いて、積分動作によって、出力が、一定速度で変化します。
◆ PI 動作の制御応答を、図 9.2-351に示します。なお、図 9.2-349 の青色(▽)も、PI 動作です。この図 9.2-349 の積分動作(△黄色)とPI 動作(▽)とを比較して、積分動作よりも、PI 動作の方が、応答が、大幅に速くなっていることが、分かります。この理由から、実際には、PI 動作が、多く使用されており、積分動作単体は、あまり多くは、使われていません。
◆
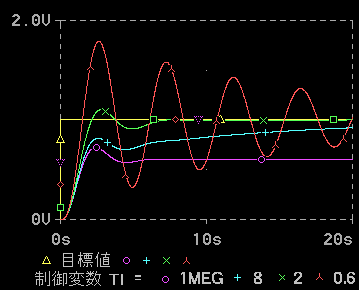
図の、○(藤色)は、P 動作だけで、積分動作を含みません。したがって、オフセットがあります。藤色以外の波形は、PI 動作の波形です。PI 動作では、オフセットは、ゼロになります。ただし、+(水色)は、積分の効きが不十分なので、オフセットが無くなるまでに、長い時間が掛かります。
図の緑色(□)は、ほぼ最適と考えられる制御応答です。赤色(∧)は、積分動作が効き過ぎために、振動的になっています。さらに、積分時間を短くすれば、ハンチングします。
◆
図で、1 MEG というのが、あります。これは、積分無しの、比例制御です。積分動作は、その制御演算式から分かるように、積分時間を無限大にすれば、積分無しになります。この図 9.2-351 では、1 MEG となっている波形です。
この波形は、回路シミュレーションの波形です。ここで使用している回路シミュレーションでは、値を無限大にできないので、無限大の代わりに、充分大きな値、1 MEG(106) を使用したのです。
◆
PI 動作は、オフセットをゼロにすることができ、かつ、制御応答が、比較的速いという特徴を持っていますから、広く使用されています。ただ、欲を言えば、P 動作と比べると、制御応答が、遅いという、欠点があります。
◆
この欠点を減らし、制御応答を、より速くしたものが、PID 制御 (PID 動作 )です。PID 動作は、PI 動作に、さらに、微分動作 (伝達関数で Td s) を追加した制御演算式です。定数 Td のことを、微分時間 といいます。
◆
微分動作(Td s)の特性を、図 9.2-352 に示します。微分動作のステップ応答(図の上側)は、高さが無限大で、幅が無限小のパルスです。周波数応答(図の下側)では、周波数が無限大のとき、そのゲインは、無限大になります。
◆
この、微分動作は、制御応答を速くして、制御成績を高める効果が、あります。しかし、微分動作単独では、制御能力が、ありません。また、微分動作単独の、上記の制御要素 Td s は、実際に回路を作ることも、できません。
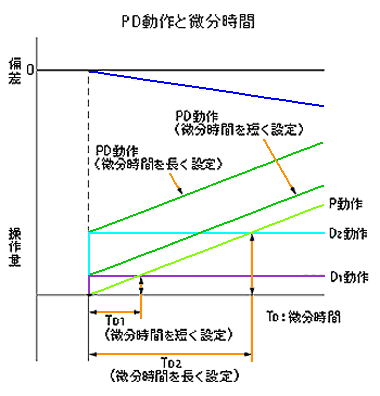
微分動作は、単独では制御能力が、ありませんし、作ることもできませんから、比例動作と組み合わせて、PD 動作 として、使用します(図 9.2-353)。図は、偏差が一定速度で変化した場合を示しています。一定底度で変化する関数のことを、ランプ関数 といいます。図には、微分時間が長いものと、短いものと、2 つの波形を示してあります。
◆
図において、偏差がゼロの状態から、偏差が発生し始めると、先ず、微分動作が働いて、偏差の変化速度に比例して、操作量が、ステップ状に変化します。その後、P 動作によって、偏差の大きさに比例した操作量が加わります。操作量は、一定速度で変化します。
◆
PD 動作における、微分動作の部分は、1 次フィルタと組み合わせた、実用微分動作 を使う必要があります(図 9.2-354)。上側は実用微分動作の伝達関数、中央は、そのステップ応答、下側は周波数応答です。
◆
実用微分動作は、上図中央のステップ応答から分かるように、パルスの高さが有限で、時間的にも広がりのある波形です。
実用微分動作の周波数応答(図 9.2-354 の下側)を、微分動作単独の周波数応答(図 9.2-352 の下側)と比較すると、実用微分動作は、高い周波数において、ゲインが、20 dB で頭打ちになっており、位相も、90°から 0°へと、低下していることが分かります。
◆
実用微分動作が、このような波形になっているのは、微分効果を高めるためのものでは、ありません。この波形ゲインが頭打ちになる波形は、ノイズ対策の、ためのものです。ノイズ対策を施したことによって、微分効果そのものは、低下しています。
◆
ノイズは、高い周波数ほど、伝わり易く、載り易いという性質を持っています。このため、実際の制御系においては、制御を行うのに必要な周波数帯域の信号よりも、高い周波数に、ノイズが、多く載ってきます(このホームページの別の講座「良く分かる実用ノイズ対策講座」の、1.(3)、1.(3-E-a) 参照)。
◆
生の、微分動作は、高い周波数のゲインが大きいために、上記の高周波ノイズを、不当に増幅します。その結果として、信号がノイズに、埋もれてしまいます。これでは、正常に動作できません。
◆
制御動作が、正常に動作するように、微分動作では、フィルタを、併用しているのです。図 9.2-354 における、1 次フィルタは、このノイズをカットして、微分動作を正常に、動作ささせるためのものです。
◆
微分動作の効能は、予知動作 にあります。比例制御は、現在の制御変数の値によって、制御出力の値が決まります。PI 動作は、制御変数の、過去の値の影響を反映しています。積分は、積分の定義それ自体が、過去の値の蓄積です(図 9.2-355)。図には、この後で述べる、PID 動作も入っています。
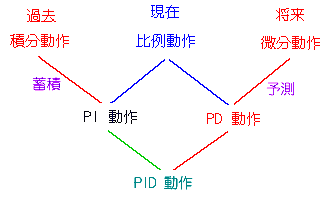
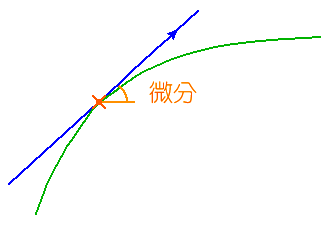
◆ 微分動作は、現在変化しつつある、制御変数の、方向とその大きさとによって、将来の値を予測して、それを操作変数の大きさに反映させた 制御です。すなわち、現在の制御変数の値が変化変化している方向に、制御変数の値が、より大きく変化するように、操作変数の値を、一時的にパルス状に、変化させます(図 9.2-354 の中央の図 参照)。微分動作は、図 9.2-356に示すように、波形の傾斜の大きさに比例して、操作変数を、変化させます。
◆
現在多く使われている制御演算式は、P 動作(比例動作)、I 動作(積分動作)、D 動作(微分動作)を組み合わせた、PID 動作です。PID 動作の制御演算式(伝達関数)は、
Kp (1 + 1/(Ti s) + Td s) ・ ・ ・ (9.2.4)
Kp (1 + 1/(Ti s))(1 +Td s) ・ ・ ・ (9.2.4)’
の、2 種類があります。式(9.2.4) は、教科書などに出てくる基本式ですが、実際には、とくにアナログ制御では、式(9.2.4)’が、多く使われています。どちらを使用しても、特性の差は、実用上、ほとんど、ありません。ここでは、式(9.2.4)’を使って、説明します。
◆
PID 制御の周波数応答を、図 9.2-357 に示します。図の上側はゲイン、下側は位相です。図は、微分時間 Td を一定とし、積分時間 Ti を変化させたものです。
◆
図において、周波数が高い領域(図の B)で、ゲインおよび、位相が、周波数と共に増加しています。この領域が、微分動作が効果を出している領域です。微分動作の効能は、位相の進みにあります(コラム 9.2-22 参照)。ゲインが周波数と共に増加しているのは、好ましくない、副作用です。
◆
また、周波数の低い領域(図の A)で、ゲインが周波数と共に増加し、位相は、マイナスの方向で、その絶対値が増加している部分があります。この領域が、積分動作が効いている領域です。積分動作の効能は、ゲインの増加にあります(コラム 9.2-22 参照)。位相がマイナスの方向に、絶対値が増加しているのは、やむをえない副作用です。
◆
以上を総合して、制御演算式の優劣を、まとめて示すと、図 9.2-358 のようになります。制御能力が、× は、制御する能力がありませんから、使用できません。
★ 成績は、幼稚園の入学試験から始まって、学校を卒業するまで、付いて回ります。就職しても、また、成績が問題になります。嬉しくはありませんが、成績は、人生に、付いて回ります。

★ フィードバック制御も、制御成績 で、評価されます。自動制御は、目的用途が、いろいろありますから、制御成績の評価方法も、自動制御の、目的用途によって、異なります。
それは、それで良いのですが、何か、汎用的な評価方法が 在った方が便利です。
★ 制御成績は、偏差で、評価されます。その偏差に関して、下図のように、いろいろな評価基準が あります。
★ 許容誤差 は、その制御対象において許容される、偏差の大きさです。図に示されるように、最初の山と谷とを無視した、後の値で、評価します。
★ 行き過ぎ時間 は、応答における、最初のピーク位置までの時間です。行き過ぎは、通常、図に示したように、最初のピークで発生します。行き過ぎが発生しない波形のときは、行き過ぎ時間も、存在しません。
整定時間 は、最後に許容誤差の半内に収まったときの(すなわち、これ以降は許容誤差の範囲内にあるという)時間です。
★ 行き過ぎ量 は、行き過ぎ時間内における、最大偏差量です。図に示すように、通常は、最初のピークです。これも、行き過ぎが発生しない場合には、存在しません。
★ オフセット は、すでに示したように、定常状態 に達した後の、偏差量です。
これらを総合した、制御成績の評価量として、2 乗誤差面積 が、あります。2 乗誤差面積は、制御成績の評価だけでなく、広く一般に使用されている、評価関数 です(下式)。
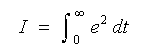
★ この評価関数は、偏差を 2 乗しています。したがって、単純に絶対値を平均したものに比べて、より大きな偏差の方が、大きな重みで、評価されています。
この評価関数に基づいた最適応答の波形は、ほぼ、上図の波形となります。振動的であって、行き過ぎもある波形です。
★ この波形は、結果として、あるピークに対して、その次のピークは、振幅が、約 1/4 となります。
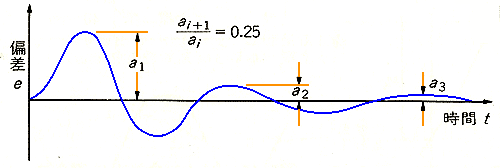
逆に、ピーク間の振幅が、約 1/4 となるように調整すれば、最適応答に、ほぼ近い応答が、得られます。最適化の手法を使わないで、トライアルで調整を行うとき、ピーク間の振幅が、約 1/4 となるように、調整すると良いでしょう。
★ 制御対象によっては、振動的なったり、行き過ぎが発生しては まずい 場合があります。このような、制御対象では、振動的にならないとか、行き過ぎにならないという条件付で、評価関数を評価する必要が、あります。
★ さて、PID 動作では、制御パラメータが、比例ゲイン、積分時間、微分時間と、3 つあります。
一般に、調整を行うとき、調整を行うパラメータの数が、1 または 2 のときは、トライアル で、最適なパラメータ値を捜し求めても、それほど大きな手間は、掛かりません。しかし、パラメータの数が、3 つ以上になると、トライアルでは、負担が大きくなります。
★ この意味で、PID 制御では、最適応答 の制御パラメータを求める手法が、欲しくなります。PID 制御は、多く使用されていますから、最適解を求める手法も、多くあります。
★ ここでは、それらの中から、歴史的にも有名な、限界感度法 について説明します。
限界感度法は、PID 動作だけでなく、PI 動作にも適用されます。
★ 先ず、限界感度法の手順を示します。
(1) 簡単な現場実験を行います。この現場実験は、自動制御を行っている状態で、実行できますから、制御を大きく乱すことが、ありません。
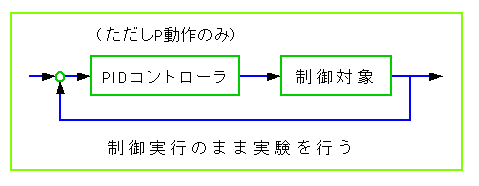
★ 現場実験の内容は、次の通りです。

★ 比例ゲイン Kp を増加させると、制御応答は、下図のように変化します。
★ この制御実験では、水色のような、振幅を増大させるような実験は、行う必要がありません。藤色の持続振動の状態までで、実験を打ち切りますから、制御系を不安定にすることは、ありません。
持続振動まで持ってゆくことが心配なら、その少し前の、若干振動が減衰している状態で打ち切っても、実用上問題の無いデータが得られます。
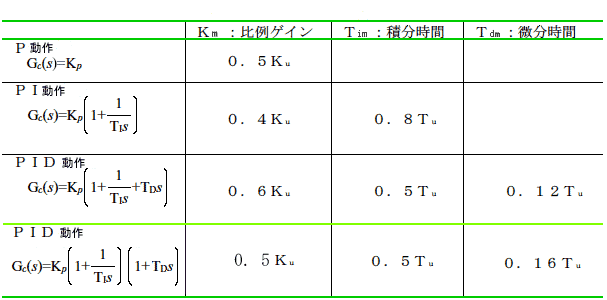
★ (2) この、持続振動の状態で、そのときの、比例ゲインの値 Ku と、振動の周期 Tu とを測定します。Ku を限界感度 、Tu を限界周期 と呼びます。
下記の限界感度の表によって、最適な比例ゲイン Km、最適な積分時間 Tim、最適な微分時間 Tdm を求めます。
なお、表の上 3 段は、限界感度法の開発者である、ジーグラ・ニコルスによる値ですが、最下段は、宮崎技術研究所が、独自に求めたものです。
★ 制御対象の特性は、いろいろです。限界感度法は、制御対象の特性に関わらず、同じ制御パラメータの値を、選定します。実際には、制御対象の特性が異なれば、最適な制御パラメータの値は異なるはずです。限界感度法では、この違いを無視して、一律の値になっています。また、実際には、外乱の入力点に違いによっても、制御応答が異なります。
★ 逆に言えば、限界感度法は、それほど精度が高いものではなく、一応の目安を与えるものです。また、最適値から多少外れていても、制御成績が著しく悪くは、なりません。制御パラメータの値を変えたときの、評価関数の値は、シャープな特性ではなく、下図のような、鍋底形、または、それに近い ゆるい 特性のものが、多いと考えられます。

★ 周波数応答(次のコラム 9.2-22 参照)は、制御対象の特性を、きめ細かに表現することができます。
★ また、周波数応答の、もう一つの大きな特徴は、フィードバック制御において、制御ループを開いたときの特性から、ループを閉じて、自動制御を行ったときの応答を、推定することが できる、ことにあります。
★ 制御ループを開いたときの伝達関数のことを、一巡伝達関数 といいます。一巡伝達関数は、どこでループを開いても、一巡伝達関数自身の特性は同じですが、下図のように開くと、分かり易いと思います。
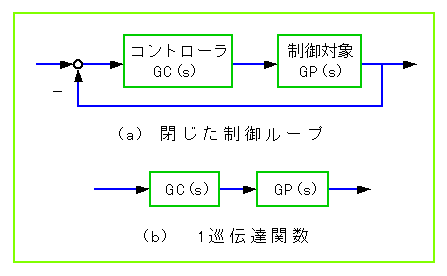
★ 一巡伝達関数を使用すると、フィードバック制御系において、ループを開いたときの特性から、ループを閉じたときの特性を、容易に推定することができます。ループを閉じたときの特性は、直接計算することもできますが、ループを閉じたときの特性の計算よりも、ループを開いた状態を計算する方が、はるかに計算が楽です。
★ 簡単のために、コントローラは、P 動作であるとします(図 a )。
★ この周波数応答は、図 . b の通りです。比例ゲイン KP は、図に示すように、KP = 1、1.3、3、10、24 です。
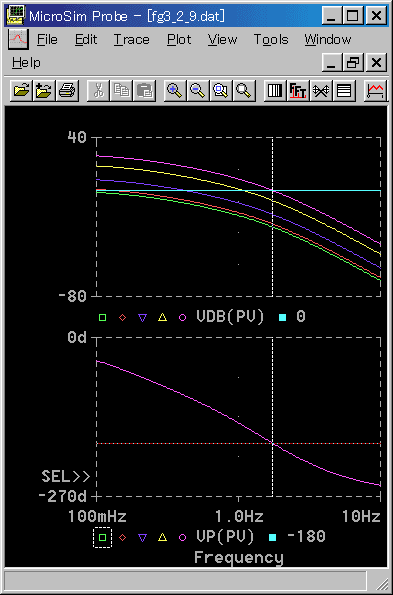
★ 図で、比例ゲイン KP=1 は、制御対象の特性そのものです。
ここで、比例ゲイン KP を変化させて、位相が -180°の周波数のところで、ゲインが、ちょうど 0 dB になるように調整します(図の KP = 24)。
★ この状態で、ループを閉じ、最初の入力として、下図の黒線のような、半正弦波を、図 . a の A に加えます。
★ 加えた信号は、ループを一巡して、図の a の B まで戻ってきます。このループは、フィードバック制御のループですから、値がマイナスされて(図 a の C)、フィードバックします。以下、D、E、のように、なります。
★ 以上から、ループのゲインが 1 のときは、何らかのきっかけががあれば、持続振動が発生することが、分かります。また、ループのゲインが、1 よりも小さいときは、きっかけがあって、震度を開始しても、減衰振動となり、振動は消滅するであろうことが、推定されます。また、ループのゲインが 1 よりも大きいときは、振動の振幅は増大します。しかし、何らかの制限がありますから、その制限に引っかかって、持続振動になります。
★ 外力にっよって引き起こされる振動は、その振動要因が無くなっても、持続振動の条件であれば、振動を続けます。これが、発振の条件です。
★ さて、持続振動となる条件は、系が振動を起こしても、その振動が減衰してしまう条件と、振動の振幅が増大する 不安定な条件との、ちょうど中間に位置します。これを、安定限界 といいます。
★ 系を安定に動作させるためには、安定限界の中に入っていることが、必要です。この案て限界よりも安定な範囲内は、安定ですが、安定限界から、離れているほど、安定な程度が高くなります。逆に、安定限界から、不安定な方向に、大きく隔たっているほど、振動の振幅増大が著しくなります。
安定な程度を安定度 といいます。安定度は、振動の振幅の減衰率で表すことができます。
★ 制御応答の図において、緑色が、最も安定度が高く、以下順に安定度が低くなり、藤色が安定限界です。そして、水色は不安定です。
この安定度を目安として、最適な制御パラメータを設定する手法があります。制御系の動作点が、安定限界の上にあれば、持続振動です。この安定限界から、安定の方向に、遠ざかるほど、安定の程度は増加しますが、制御の即応性は悪くなります。したがって、この中間で、ちょうど最適な制御応答が得られるはずです。
★ この考え方から、ゲイン余裕と位相余裕とを使って、最適な制御応答を求めることができます。下の周波数応答の図に示すように、ゲインが 0 dB のときの周波数における位相の値を位相余裕 といいます。また、位相が -180°のときの周波数におけるゲインの値を、ゲイン余裕 といいます。
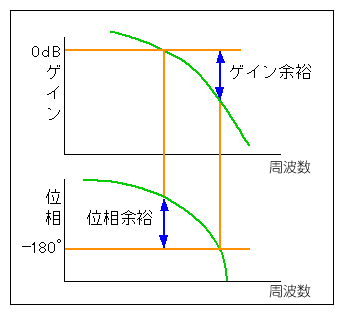
★ このゲイン余裕と位相余裕の値を、下図のようにすることによって、最適応答が得られます。ただし、一応の目安です。真に最適にするためには、さらにトライアルするか、別の手法を使う必要があります。
| − | 位相余裕 | ゲイン余裕 |
| プロセス制御(定値制御) | 16〜80° | 3〜9 dB |
| プロセス制御(追値制御) | 50°以上 | 4〜9 dB |
| サーボ(機械制御) | 40〜65° | 12〜20 dB |
★ なお、最適な PID 制御パラメータを求めることだけが、目的の場合には、周波数応答は、安定限界付近の周波数応答波形が必要であり、それ以上広範囲のデータは必要ありません。
★ ホップ、ステップ、ジャンプ。これは三段跳びの技法です。三段跳びでは、最初の助走に次いで、第 1 歩のホップ、第 2 歩のステップ、そして最後のジャンプへと続きます。下の写真は、織田幹雄氏の三段跳びです。織田幹夫氏は、きき足が左なので、ホップ(左足)、ステップ(左足)、ジャンプ(右足)と、飛ばれました。

★ 3 という数字は、何故か、魅力のある数字です。三種の神器、毛利元就の三本の矢、果は、三角関係にいたるまで、多く使われている数字です。
三角形は、幾何学的には、特別な多角形です。三角以下では、面を作れません。四角形以上では、形が決まりません。三角形は、3 辺の長さを与えれば、形が確定します。
★ さて、制御応答 について、説明しましょう。先ず、ステップ応答ですが、ステップ応答は、周波数応答と並ぶ、代表的な、入力波形です。ランプ関数を入力とするランプ応答 も、典型的な入力波形として使われていますが、ステップ応答や、周波数応答に比べると、使われる頻度は、大幅に少なくなっています。
★ ランプ応答、ステップ応答および、周波数応答を、比較して見ましょう。図で、表現力は、制御対象による特性の違いが、応答波形を見て、どの程度良く識別されるか、ということです。

★ 周波数応答は、最も表現力が高い方式ですが、分かり難いという欠点があります。周波数応答(周波数特性)については、3.1.(2-C) で説明しましたが、ここで、もう少し、補足しておきましょう。
★ 周波数応答の入力波形は、正弦波形です。正弦波形を入力し始めたときは、過渡的な応答波形がありますが、やがて、定常状態となります。定常状態では、出力波形も、正弦波形で、その周波数は入力と等しく、振幅と位相は入力と異なります。
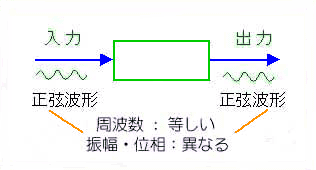
★ この定常状態になった後に、入力と出力の正弦波形の振幅比(ゲイン)と、位相差とを入力周波数でプロットしたものが、周波数応答です。
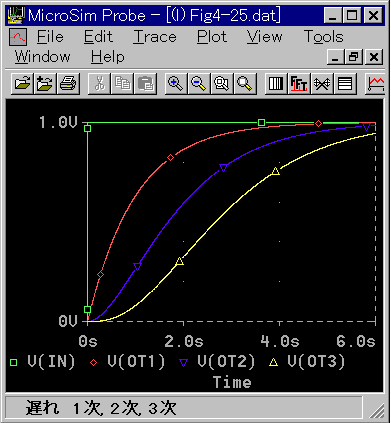
★ ステップ応答と、周波数応答の表現力の差を、見てみましょう。下図は、1 次、2 次および 3 次フィルタのステップ応答です。1 次フィルタは、最初から立ち上がっているのに対して、2 次以上では、最初は、水平からスタートしています。1 次と 2 次以上との波形の差は、明確ですが、2 次と 3 次または、それ以上は、定量的な差があるだけで、定性的な違いは、認められません。
★ これに対して、周波数応答では、下図が 1 次フィルタ、その下が 2 次フィルタで、次数による違いが、はっきり分かります。1 次フィルタの高周波(阻止域)におけるゲインの減衰量は、-20 dB/dec、位相は -90 °/decです。これに対して、2 次フィルタの阻止域は、ゲインの減衰量が、-40 dB/dec、位相が -180 °です。さらに一般に n 次フィルタでは、ゲインの減推量が -20 n dB/dec、位相が -90 n °/dec となります。
★ 周波数応答は、複雑で分かり難いにも関わらず、多く用いられています。この理由は、上記のように、特性の違いが、周波数応答の波形に、良く現れるからです。
★ ディジタルの反対語は、アナログです。アナログとディジタルについては、コラム 2.2-1a でも説明しました。
★ 自動制御にも、アナログ制御とディジタル制御とが、あります。
アナログ制御の理論は、伝達関数をベースにしています(9.2.(2-C-l) 参照)。
★ ディジタル制御においても、伝達関数の考え方を適用するのが、便利です。ただし、ディジタル制御では、アナログの伝達関数の代わりに、パルス伝達関数と呼ばれているものを、使用します。
★ アナログ系においては、遅れがある制御要素は、積分で表すことが、できました。遅れがあるということは、過去の変数の値が現在に影響を及ぼしている、ということです。
★ ディジタル系においても、遅れがある制御要素は、過去のサンプル値を加算した形で、表すことができます。下図において、ti は i 番目のサンプリング時刻、Xi は ti における入力変数の値、yi は ti における出力変数、θ はサンプリング周期です。
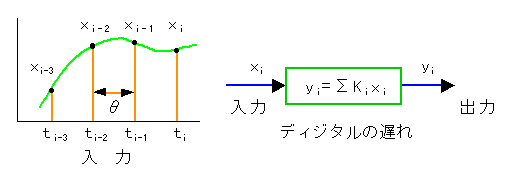
★ 出力 yi は、
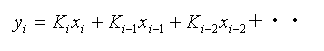
となります。ここで ki は重みです。この重みの大きさを変えることによって、いろいろな特性の遅れを作ることが、できます。
★ 上記の式で表される制御要素は、ブロック図で表すと、
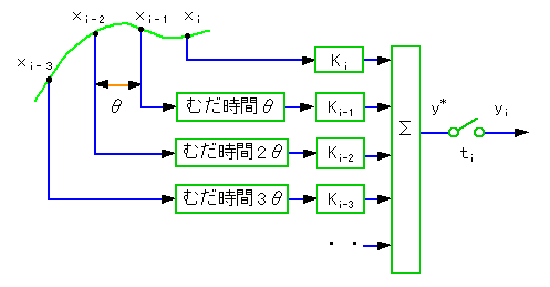
のようになります。
★ 図に、スイッチの記号があります。これは、スイッチではなく、サンプリングを表す記号です。サンプリングの動作は、あたかも、常時開のスイッチを、サンプリングの瞬間だけ閉じたのと、同じように見えます。このことから、サンプリングの記号は、スイッチの記号と、同じ記号を使用します。
★ また、図には、無駄時間、というのが あります。無駄時間 は、一定の時間(下図では、DT)ずれを作る、制御要素です。
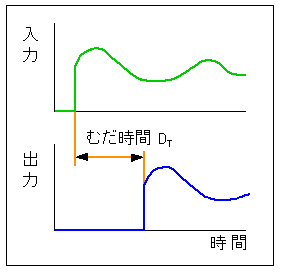
★ 無駄時間は、伝達関数で表すと、
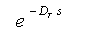
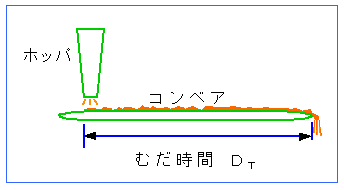
です。無駄時間は、周波数応答では、ゲイン(振幅)は、1 (0 dB) で、位相だけが、急激に遅れます(下図)。
★ 無駄時間特性を有する、制御対象は、たとえば、コンベアのシステムが、あります。下図において、ホッパから、コンベアに排出された原料は、コンベアに落ち、コンベアに乗って、