

◆
データコンバータ は、データの種類を相互に変換します。ソフトウェアにも、データコンバータがあります。ソフトウェアのデータは、種類がいくつもありますから、データコンバータの種類は、沢山あります。
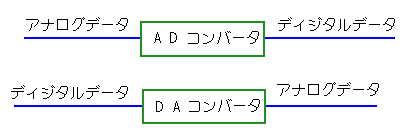
しかし、ハードウェアの IC では、データコンバータは、アナログデータをディジタルデータに変換する、アナログディジタル コンバータ (A D コンバータ 、アナログ ディジタル 変換機(器 )、A D 変換機(器 ) 、ADC )と、ディジタルデータをアナログデータに変換するディジタル アナログ コンバータ (D A コンバータ 、ディジタル アナログ変換機(器)、D A 変換機 (器 )、DAC )の 2 種類です(図 6.4-1)
。

◆
データコンバータは、アナログとディジタルとの相互変換ですから、アナログデータとディジタルデータの両方を取り扱っています。しかし、分類上は、通常、アナログ IC に含めています。
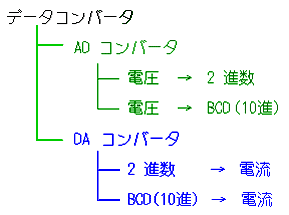
データコンバータの、アナログ量は、電流または、電圧が使用されます。ディジタル量には、2 進または 10 進(BCD が多い)を使用します(図 6.4-2)。
◆
ここでは、時間と共に変化する量、すなわち、時間を独立変数とする変数を、考えます。データコンバータを使用する場合、通常は、ある特定の 1 時点のデータではなく、時間と共に変化する量を、逐次処理します。したがって、時間と共に変化する量を、考える必要があります。
◆
アナログ量の特徴は、連続であるということです。これに対して、ディジタル量は、飛び飛びの、非連続 量です。すなわち、AD 変換することによって、連続量であるアナログ値は、デジタルという非連続量に変換されます。連続量から、飛び飛びの値を取り出すことを、量子化 といいます。量子化の言葉を使えば、AD 変換は、量子化を行っています。
◆
量子化の荒さ、すなわち、連続量を、何ビットに変換するかを、量子化ビット数 といいます。
◆
アナログをディジタルに変換するのには、時間がかかります。ある 1 つの値を変換してから、次の値を変換するのは、さらに、その後になります(図 6.4-3)。
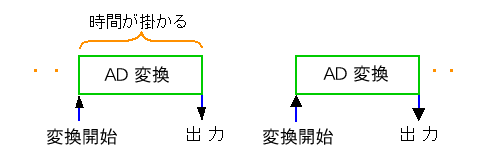
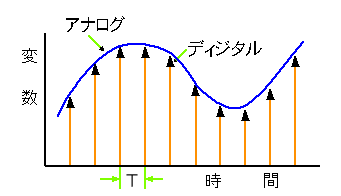
◆ したがって、AD 変換すると、値が量子化されるだけでなく、時間的にも、飛び飛びになってしまいます(図 6.4-4)。
◆
このように、アナログの連続量から、飛び飛びの時点の値を取り出すことを、サンプリング (標本化 )といいます。サンプリングは、時間の量子化です。
サンプリングの、時間間隔は、一定である必要は、ありません。しかし、通常は、図のように、一定時間間隔 T 毎に、サンプリングを行います。一定時間間隔の方が、簡単ですし、その方が、使い易いことが、多いからです。
◆
サンプリングの時間間隔を、サンプリング周期 (サンプル周期 )といい、サンプリング周期 T の逆数 f = 1/T を、サンプリング周波数 (サンプル周波数 、サンプリングレート 、サンプルレート )といいます。
◆
以上のように、アナログ量をディジタル量に変換することは、時間軸に対しても、変数軸に対しても、共に非連続にすることです。非連続にするということは、飛び飛びにするということですから、それに、起因する誤差が発生します。
◆
変数軸の誤差を減らすためには、まず第 1 に、アナログ〜ディジタルの変換桁数 (変換ビット数)を、多くします。AD コンバータで発生する誤差の要因は、いくつかありますが、最も基本となる誤差は、変換桁数の粗さによるものです。
◆
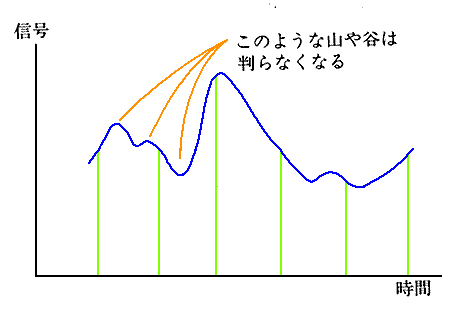
時間軸の誤差を減らすには、サンプリング周期を短くする必要があります(図 6.4-5)。
◆
サンプリング周期が、信号の周波数帯域に対して長いと、単に途中の値が分からなくなる、だけでなく、もっと激しい、嫌な現象が、現れます。
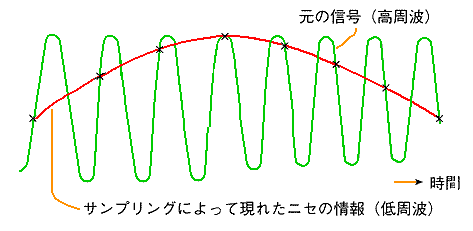
本来信号には存在しない、偽の情報を掴まされて、しまうのです。この偽の情報のことを、エリアス (エイリアス 、アリアス )といいます(図 6.4-6)。エリアスは、偽という意味の言葉です。
◆
図から、想像されるように、エリアスは、元のアナログ信号の周波数帯域に対して、サンプリング周波数が、十分に高くないときに、発生します。逆にいえば、サンプリング周波数を、十分に高くしてやれば、エリアスを、防ぐことが、できます。
◆
この状況を、定量的に示したものが、サンプリング定理 (シャノンの定理 )と呼ばれている定理です(ただし、シャノンの定理と呼ばれているものには、複数ありますから、サンプリング定理の言葉を、使う方が、良いでしょう)。
◆
サンプリング定理は、
「元の信号の情報が、失われないように、サンプリングするためには、元の信号に含まれる、最高周波数を、fmax とすれば、2 fmax 以上の周波数でサンプリングする必要がある」
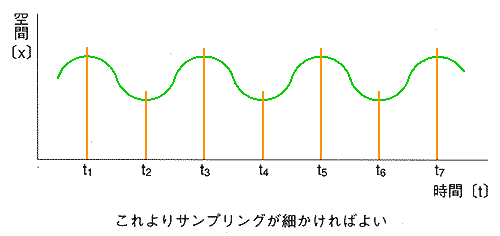
というものです。図 6.4-7 は、サンプリング定理ギリギリの周波数でサンプリングしたものです。
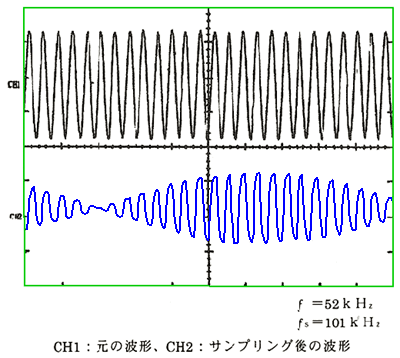
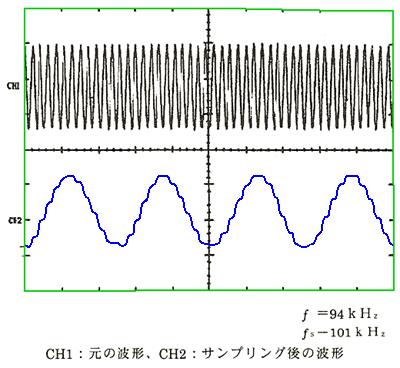
◆ サンプリング定理に違反して、エリアスが発生したときの波形を、図 6.4-8 に示します。どちらも、上側が元の波形、下側がサンプリング後の波形です。
◆
サンプリング定理よりも、低い周波数でサンプリングすることを、アンダーサンプリング 、サンプリング定理よりも、高い周波数でサンプリングすることを、オーバーサンプリング といいます。
◆
当然、アンダーサンプリングは、実用になりません。アンダーサンプリングにならないように、サンプリングする、必要があります。
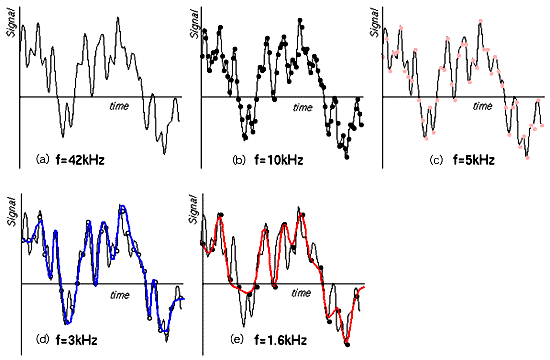
アンダーサンプリングによる、変換品質の低下の例を、図 6.4-9 に示します。図の(a)は、元の波形(実は、十分に高いサンプリング周波数で AD 変換したもの)で、信号の最高周波数は、5 kHz です。(b)は、サンプリング定理に適合した、10 kHz サンプリング、(c)〜(e)は、アンダーサンプリングです。(c)では、波形の劣化は、それほど目立ちませんが、(d)、(e)と、高周波の情報が、急速に、失われていることが、分かります。
◆
実際の、観測波形には、欲しい信号だけでなく、ノイズが重畳しています。したがって、サンプリングに当っては、ノイズ対策を考える必要があります。
通常、ノイズの周波数帯域は、信号よりも、高周波です。信号に対して、サンプリング定理に違反しないように、サンプリングしても、ノイズに対しては、サンプリング定理に違反していることが、考えられます。ノイズが、サンプリング定理に違反していても、差し支えないとも考えられますが、そう、簡単には行きません。
◆
エリアスは、図 6.4-6、などから分かるように、元の信号よりも、低い周波数に化けます。したがって、信号よりも高周波のノイズが、エリアスによって、信号周波数のノイズになって、しまいます。
ノイズは、通常、信号よりも高周波ですから、ローパスフィルタで、取り除くことができます。しかし、サンプリングによって、高周波のノイズが、信号周波数に化けてしまったら、手の打ちようがありません。
◆
サンプリングにおける、ノイズ対策の方法には、図 6.4-10 に示す方法があります。
◆
(a)は、ノイズの周波数帯域が、欲しい信号に対して、あまり高くないときに、使用できます。欲しい信号に対して、ノイズ周波数が大幅に高いと、ノイズを AD 変換するために、高速の AD 変換機が必要となり、高価になる恐れがあります。一般に、ノイズの周波数は、欲しい信号の周波数よりも、はるかに高いことが多いので、このような場合には、実用性がありません。
この方式を使用すれば、ノイズを含み、すべての信号が、サンプリング定理に、違反していませんから、エリアスは発生しません。したがって、AD 変換した後に、すべてを、ディジタル演算で処理することが、できます。
◆
(b) 欲しい信号の周波数帯域と、ノイズの周波数帯域とが、かなり、はなれていれば、アナログフィルタは、簡単なフィルタ(たとえは、パッシブの 1 次フィルタ)を使用することが、できます。
◆
(c) 上記(a)または(b)の対策は、簡単ですから、望ましい方法です。しかし、欲しい信号の周波数の上限と、ノイズ周波数の下限とが、接近しているときには、この(c)の方式を、使用することになります。この方式を使用した AD 変換機を、オーバーサンプリング形 AD 変換機といいます。オーバーサンプリング形 AD 変換機 の構成を、図 6.4-11 に示します。

◆
ディジタルフィルタ は、ディジタル演算 によって作るフィルタです。ディジタル演算は、アナログ演算と比べて、容易に、かつ安価に、高度な演算を行うことができます。
とくに、最近は、多くの機器にコンピュータ(多くはマイコン)が、内蔵されています。このマイコンを利用して、ディジタル演算による、ディジタルフィルタを、構成することが、できます。
また、観測した(AD 変換した)データを、パソコンなどのコンピュータに取り込んで、ソフトウェアで、データ処理を行うことが多くなっています。このときは、データ処理の中で、ディジタルフィルタを、使用することができます。
[注 1]
ディジタル演算は、5.1.(2-A) で、論理演算であると、定義しました。論理演算の意味でも、使われていますが、ディジタル演算は、より一般には、論理演算だけでなく、算術演算も含んだ、広い意味でも、使われています。
[注 2] コンピュータでは、一般に、高度な演算も、算術演算に変換して、算術演算の形で、実行します。デイジタルフィルタも、算術演算をとります。