◆
フィードバック制御は、簡単なオンオフ制御などを除いて、多くは、PID 制御が、使われています。しかし、とくに制御が難しい制御対象や、厳密な制御が必要な場所には、PID 制御よりも、さらに高度な制御演算式や、複数の制御を組み合わせた制御などが、使われています。
◆
単純な PID 制御よりも、何らかの意味で、高度な制御のことを、アドバンスト制御 と呼んでいます。ここでは、アドバンスト制御について、説明しておきます。アドバンスト制御は、ごく簡単なものは、アナログ制御でも、使用されていますが、多くは、ディジタル制御で、用いられています。
◆
アドバンスト制御には、いろいろな制御方式があります。その中で、代表的なものを、図 9.2-358 に示します。
◆
微分先行形 は、PID 制御を若干改良したものです。
制御応答には、設定値(目標値)を変化させたときの応答と、外乱が入ったときの応答とがあります(図 9.2-359)。
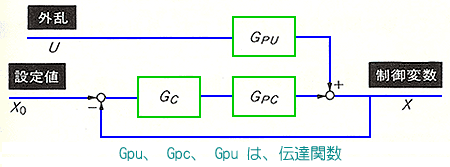
◆ 目標値変化に対する応答は、
外乱に対する応答は、
となりますから、等しくありません。
◆
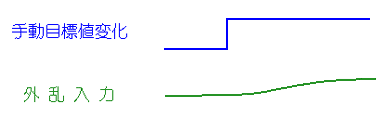
このため、目標値変化、外乱の、どちらか片方に合わせて PID 制御のパラメータを調整すると、他方に対しては最適な応答から外れてしまいます。しかも、定値制御の場合に、手動で目標値を変えるときは、ステップ状の変化になるのに対して、外乱は一般に、ゆっくりした変化です(図 9.2-360)。この違いも、あります。
◆
とくに、制御演算式に、微分動作が含まれているときに、手動で目標値を変えたときの、制御応答が、問題になります。外乱に対する制御応答が、良好になるように、PID 制御のパラメータを設定すると、ステップ状の目標値変化に対しては、微分動作が効き過ぎて しまいます。
◆
この問題に対応するのが、微分先行形 PID 制御です(図 9.1-361)。
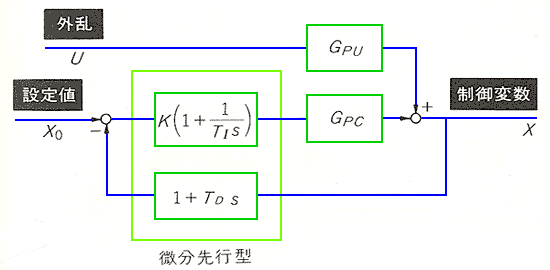

◆ 図中の式からも分かるように、設定値変化に対しては、微分先行形の方が、微分の効きが少なくなります。その結果として、制御応答は、図 9.2-362 のような、差が生じます。
◆
図の上側は通常の PID 制御、下側は微分先行形 PID 制御です。通常の PID 制御における振動が、微分先行形では、抑えられていることが 分かります。
◆
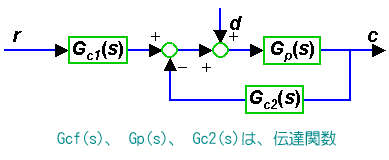
2 自由度制御 は、微分先行形を、さらに一般化した制御です(図 9.2-363)。2 つのコントローラによって、外乱に対する応答と、目標値変更時の応答を、共に最適化することが、できます。
◆
複合制御 は、複数の 制御(PID 制御など)を組み合わせた制御です。すなわち、複数の制御変数を対象として、制御を行う制御です。
多変数制御 も、複数の制御を組み合わせたものです。この意味では、複合制御と、多変数制御とは、同義語ですが、複合制御は、ある特定の組み合わせ方をしたものを指すのに対して、多変数制御は、一般化された制御演算方式のものを、意味します。
◆
先にあげた、微分先行形 PID 制御も、PI 動作のコントローラと、PD 動作のコントローラとを、複合していますから、複合制御に含めることが、できます。
2 自由度制御も、複合制御です。
◆
ここでは、上記以外の、複合制御の代表的なものについて、説明します(図 9.2-364)。

◆
カスケード制御 : フィードバック制御は、優れた制御方式であり、広く利用されています。しかし、フィードバック制御にも、欠点があります。
◆
制御対象に、外乱が入ると、偏差が発生します(図 9.2-365)。フィードバック制御は、偏差が発生してから、その偏差を打ち消すように、働きます。
◆
その偏差は、先ず外乱が発生し、制御対象の遅れ(図の GPU)を経由して、制御変数に変化が現れてから、検出されます。その偏差によって、コントローラ(図のGC)が働き、操作変数を変化させます。その影響が現れるのは、さらに、制御対象(図のGPC)を経由してから 後のことです(図の(b)のタイムチャート参照)。
◆
このように、いくつかの遅れを経由するために、制御応答には、かなりの大きさの偏差が、発生します。
図の(b) に示すように、制御変数が変化する以前に、コントローラが、外乱の存在を知り、それによって、制御操作を開始するならば、もっと、良い制御成績を収めることができる可能性が、あります。
◆
これを実現する制御方式の 1 つが、カスケード制御です(図 9.2-366)。図の上側は、カスケード制御のブロック図、下側は具体例です。
◆
カスケード制御は、図に示すように、2 重のループ になっています。内側のループをマイナーループ その調節計をスレーブ調節計 、外側のループをメジャーループ その調節計をマスター調節計 と呼んでいます。
◆
なお、ループという言葉ですが、ここの例では、文字通り環状のものという意味です。また、フィードバック制御のコントローラの台数を数えるときの、単位としても、ループが使われます。たとえば、コントローラが 3 台のとき、3 ループと、数えます。
◆
カスケード制御の主目的は、メジャーループの制御変数(この例では温度 T)を、より良く制御することにあります。マナーループの制御変数(この例では流量 F)を制御するのは、この主目的を達成するための手段です。
◆
カスケード制御が、有効に働くためには、マイナーループの応答が、メジャーループの応答に比べて、速いことが、必要です。図の場合、マイナーループは流量制御系、メジャーループは温度制御系です。流量制御系は、温度制御系よりも高速ですから、上記の条件を、満足しています。
◆
この条件を、満足しているときは、マイナーループに入った外乱(図の外乱 U1)は、マイナーループで制御され、メジャーループの制御変数(T)に、影響を与えません。
メジャーループに入った外乱(図の外乱 U2)は、マイナーループでは処理できませんから、メジャーループで制御されます。
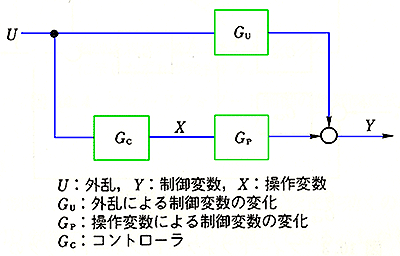
◆ フィードフォワード制御 : 外乱をいち早く打ち消す、もう 1 つの制御方式が、フィードフォーワード制御です(図 9.2-367)。ただし、フィードフォワード制御は、外乱それ自体を検出する必要が、ありますから、検出不可能な外乱には、適用できません。
◆
図において、Gc は、フィードフォワード制御コントローラです。外乱 U によって、制御変数 Y が変化しようとします。この変化を、ちょうど打ち消すように、フィードフォワード制御コントローラの特性を作ります。
◆
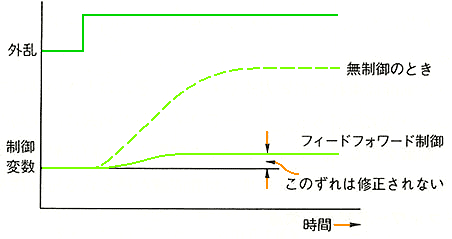
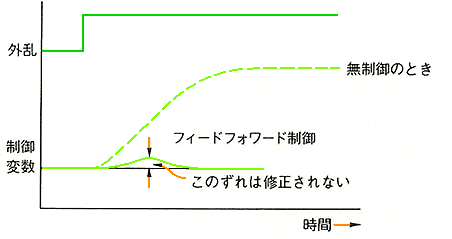
したがって、その都度、制御対象の特性に合わせたコントローラを、作る必要があります。コントローラの特性が、制御対象の特性に、マッチしていないと、その部分が、偏差となって現れます(図 9.2-368)。フィードフォワード制御コントローラの特性は、上側よりも、下側の方が、優れています。上側では、定常偏差が発生しますが、下側では、定常偏差がありません。
◆
この偏差は、制御モデル (フィードフォワード制御の制御演算式)の誤差ですから、制御モデルを修正しない限り、消すことは、できません。フィードバック制御のおける、積分動作のような、妙手は、ありません。これが、フィードフォワード制御の泣き所です。
◆
このように、フィードフォワード制御は、フィードバック制御と、その性質が逆になっています。このことから、フィードフォワード制御は、フィードバック制御と、うまく組み合わせると、優れたコントローラを、作ることが、できます(図 9.2-369)。図の上側は、ブロック図、下側は、制御例です。フィードフォワード制御の効果が大きいことが、分かります。
[図 9.2-369] フィードフォワード/フィードバック複合制御
◆ 加熱炉に、フィードフォワード制御を行った例が、図 9.2-371 です。この加熱炉の、最終的な制御変数は、加熱炉の出口温度です(図の右端の(T))。
◆
図で、一番左の、TDCS(T) とあるのが、フィードフォワード制御のコントローラで、加熱炉入り口の温度を測っています。この加熱炉入り口の温度が変動したとき、加熱炉の燃料流量を、入り口温度に対応して変化させます。この部分が、フィードフォワード制御です。加熱炉出口温度(右端の(T))の、フィードバック制御との、複合制御になっています。
◆ 非干渉制御 : 一般に、制御対象は、多変数のシステムです(図 9.2-372)。
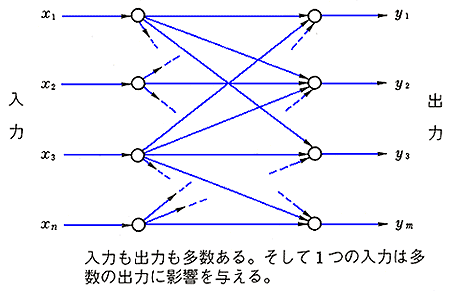
◆ この多変数のシステムにおいて、どれか一つの変数を、制御変数に選び、他の一つを、操作変数に選んで、フィードバック制御を作ります(図 9.2-373)。
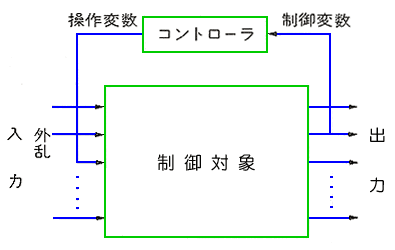
◆
操作変数に選ばなかった入力は、外乱です。制御によって、操作変数の値を変化させると、操作変数の操作によって、制御変数以外の出力も、いくつか、変化します。この制御変数および、それ以外の出力の変化は、他に対する外乱になります。
このように、多くの変数が、互いに影響し合うことを、相互干渉 といいます。制御システムでは、単一の制御ループだけでなく、この相互干渉を考慮して、制御システムを構成することが、必要です。
◆
相互干渉が強いと、各々の所に設けたフィードバック制御が、互いに影響し合います。このために、制御がうまく行かなくなる、場合があります。
簡単のために、2 変数系の例で、説明しましょう(図 9.2-374)。
◆
図の上側はブロック図、中央は伝達関数です。下側は、伝達関数をマトリッククス (行列 )の形で表したものです。多変数系は、マトリックス表示が便利です。
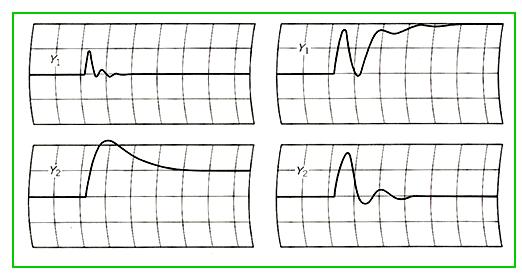
今ここで、相互干渉を無視して、2 つの制御変数(Y1、Y2)を、それぞれ、フィードバック制御してみます。ただし、その前に、比較のために、どちらか片方だけ制して、他方を無制御としたときの、制御応答を調べておきましょう(図 9.2-375)。
◆
図の左側は Y1 だけを制御して Y2 は無制御のとき、図の右側は Y2 だけを制御して Y1 が無制御のときです。当然、無制御側の制御変数は、制御した側の操作変数の変動によって、大きく変化しています。
◆ 次に、両側共に、自動制御してみます(図 9.2-376)。
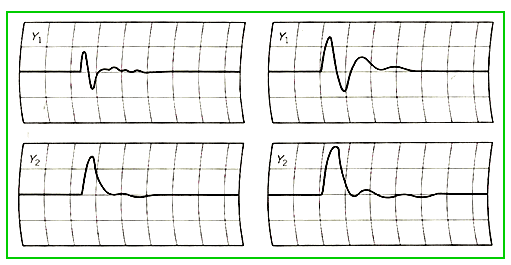
◆
相互干渉があるために、制御応答波形、とくに Y1 は、複雑な波形になっています。この例では、制御成績は、それほど悪くは、なっていません。ただし、制御対象の特性によっては、相互干渉のために、制御応答が、大幅に悪くなる場合も、あります。
◆
図 9.2-377 は、単独の制御では、正常に動作するにも関わらず、両側共に制御したために、不安定な現象を起こしてしまった例です。
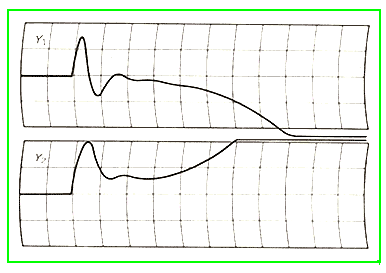
◆
ただし、この例は、特殊な条件のときであり、通常の制御系の組み方では、起こらない現象です。
相互干渉は、制御成績を、悪くするとは、限りません。場合によっては、相互干渉が、制御成績を良くすることもあります。
◆
しかし、相互干渉があると、PID などの制御パラメータを変更したときに、予期できない制御応答を、示します。この意味で、分かり難いのです。分かり難いということは、仮に、非常に良い制御応答が存在する場合であっても、その良い条件を見つけ出すことが、困難です。
分かり易ければ、その範囲内での、最適な条件を、容易に見出すことが、できます。
◆
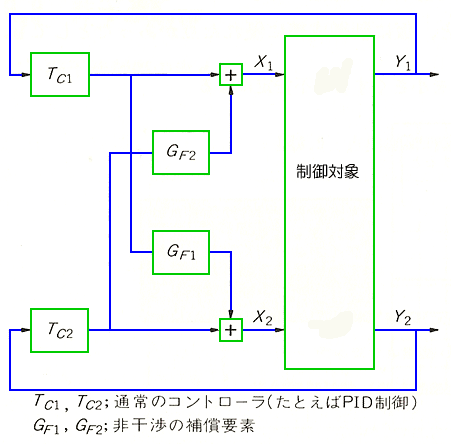
ここに、相互干渉を無くすことができる、非干渉制御の出番があります(図 9.2-378)。

◆
非干渉制御の補償要素 (図の GF1、GF2)は、フィードフォワード制御の考え方と同じです。たとえば、Tc1 の操作出力によって、X1 を変化させたとき、その X1 の変化によって引き起こされる、Y2 の変化を打ち消すように、補償要素 GF1 を介して、X2 を変化させます。
◆
非干渉制御の具体例を示します。加熱炉の例です(図 9.2-379)。この加熱炉には、4 本のコイルが入っています。
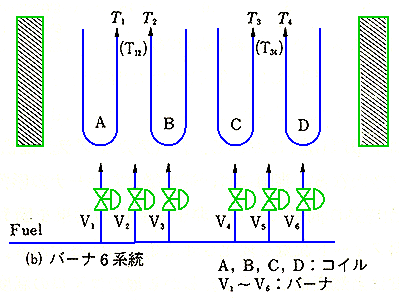
◆
コイルの出口温度は、それぞれのコイル毎に、別々に制御する必要があります。バーナーは、6 系統で、コイルとは、一対一には対応していません。コイルの加熱には、相互干渉があります。
非干渉制御を実施して、この問題の対応しています。
◆
制御対象の特性は、不変ではありません。時と共に変化します。たとえば、使い古せは、性能は低下します。周囲温度によって、特性が変化する場合も、あるでしょう。
ある特定の条件に合わせて、コントローラの制御パラメータを、最適に選んでおいても、時が経ったり、温度などの周囲条件が変化すれば、最適条件から外れてしまいます。
◆
たとえば、ロボット(図 9.2-380)は、いろいろな姿勢を取りますから、ロボット動作の特性は、ロボットの姿勢によって、大きく変化します。

◆ このようなときに、効果があるのが、適応制御 です(図 9.2-381)。図は、適応制御を、PID 制御と、対比させて、示してあります。
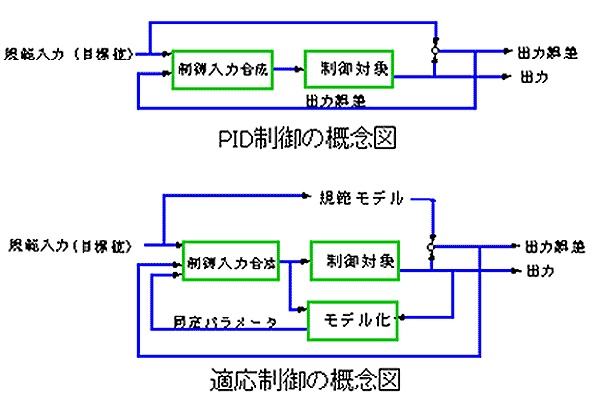
◆
ロバスト制御 の、ロバストとは、頑丈なという意味です。ロバスト制御は、制御対象の特性が、ある程度変化しても、安定に動作することを、保証する制御です。
PID 制御も、制御対象の特性が、若干変化しても、うまく制御できる性質を持っています。しかし、安定に動作することを、保証することは、できません。
◆
ロバスト制御の手法には、H∞ 制御などがありますが、具体的な説明は、省略します。車両、鉄鋼プロセスなど、とくに安定性を重視する制御対象に、利用されています。
★ フィードバック制御というと、最新の技術のように、思われます。しかし、意外にその歴史は古いのです。
★ 人間が、人力で、道具を使っていた時代には、もちろん、自動制御は、必要ありませんでした。しかし、産業革命で、動力が、使われるようになると、自動制御が必要になります。ワットは、蒸気機関を発明しました。

★ このとき、蒸気機関を制御するために、ガバナ と呼ばれるフィードバック制御装置が、登場したのです。
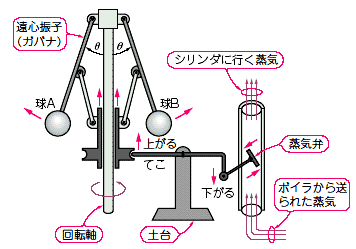
★ このワットのガバナの成功に刺激されて、その後多くのフィードバック制御が実用化しました。しかし、自動制御して見たけれども、うまく行かないという事例も、続発しました。この、うまく行かない制御を、何とかして、ものにしようとして、自動制御理論 が、誕生したのです。
★ このように、フィードバック制御は、最初、機械系を対象として、スタートしました。
機械、電気・電子の分野と並ぶ、フィードバック制御の、もう一つの応用分野が、プロセス制御 の分野です。
石油や化学のプラントは、昔は、バッチプロセスが、主体でした。バッチプロセス では、一つの装置(たとえば反応装置 )に原料を投入し、その装置の中で、複数の工程をこなして、製品を作ります。下の写真は、バッチ式反応装置です。

★ このバッチプロセスに対して、連続プロセス が、あります。連続プロセスでは、複数の装置があって、装置ごとに、異なった工程を分担します。各装置は、配管(パイプ 、パイプライン)で繋がっていて、原料は、各装置を、次々に流れてゆく間に、加工されて、製品になります。連続プロセスの代表例が、石油精製プラント です。

★ 連続プロセスでは、装置が液で満たされているものを除いて、液を取り扱っている場合は、各装置の底に液が溜まり、液面を作ります。この液面の高さは、厳密に制御する必要は、ありません。しかし、連続プロセスを、スムーズに運転するためには、液面を空にしたり、溢れさせたりすることは、許されません。
★ 制御変数は、それを無制御の状態で放置してときに、放置してままでも、ある値に落ち着く性質を持つものと、放置したときに、値が、一方的に変化してしまうものとが、あります。

★ 多くの制御変数は、放置すれば、外乱によって値が変化しますが、ある値に落ち着いて、一方的に変化し続けてしまうことは、ありません。
しかし、液面は、一方的に変化し続けてしまう場合が、あります。それは、液面それ自体が、積分特性を持っているからです。積分は、入力がゼロのときは、出力は、ある一定値を保持しますが、入力がゼロでないときは、出力は、変化し続けます。
★ 外乱が入っても、制御対象の特性によって、制御無しで、ある一定の値に近付き、一方的に変化して しまわない 性質のことを、自己平衡性 があると言います。多くの種類の制御変数には、自己平衡性があります。
自己平衡性は、下図のように例えると分かりやすいでしょう。
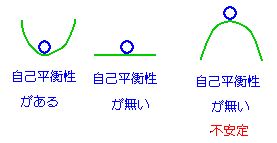
★液面の系は、それ自体では、自己平衡性がありません。フィードバック制御によって、平衡性を持たせてやらないと、安定した運転が、できません。
★ 連続プロセスにおいては、まだ、自動制御が無かった時代には、液面のところに、人が張り付いて、人力で液面制御を行っていました。この作業は、無味乾燥の作業です。
連続プロセスで、フィードバック制御が、いち早く、取り入れられたのが、省人化を目的とした、液面制御系でした。
★ 逆に、温度制御は、発熱反応などの、特殊なものを除いて、自己平衡性があります。自己平衡性が あれば、放置しても、少なくとも、危険な状態には、なりません。
ただし、温度制御は、自己平衡性は、ありますが、厳密な制御を必要とするもが多いのです。そのような場所には、早くから、温度制御が取り入れられて、いました。
★ なお、液面の系も、下図のようなときには、自己平衡性を持ちます。
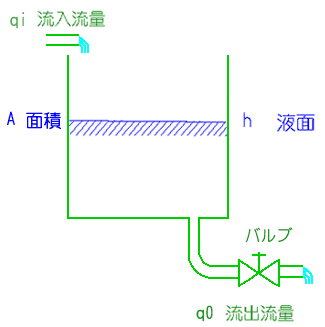
★ 上図において、バルブの開度を固定とすれば、バルブを流れる流量 qo は、バルブに掛かる差圧に比例します。バルブに掛かる差圧は、液面の高さ h (ただしバルブの位置から高さを測る)に比例します。したがって、液面系の面積を A とすれば、
A s H = Qi ー Qo
となります。ただし、s は、ラプラス変換子で、ラプラス変換領域を大文字で表してあります。
★ ここで、Qi を定数とし、Qo = k H (k は定数)とすれば、
H = 1/(T s + 1)
となり、この液面系は、1 次フィルタの式で表されることが、分かります(3.2.(2-C-a) および 3.2.(2-C-c) 参照。なお、制御の分野では、1 次フィルタのことを1 次遅れ 、n 次フィルタのことを、n 次遅れと呼んでいます。
★ さて、上記の、ガバナからスタートした、自動制御は、プロセス制御など、その適用分野を広げると同時に、制御方式と、そのバックグラウンドとなる制御理論も、各種のものが、取り入れられてきました。下図の始めの、古典制御というのが、この講座で、説明してきたものです。多変数制御は、現代制御に属します。
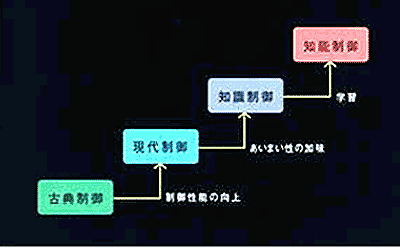
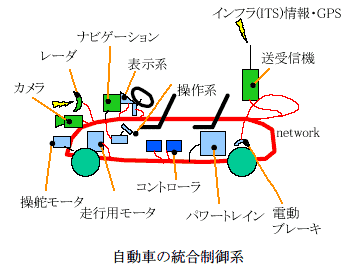
★ 自動車における制御の適用例を、下図に示します。
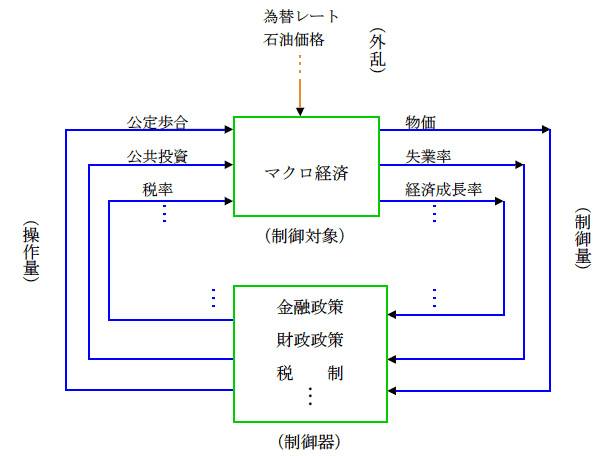
★ 経済や政策も、フィードバック制御系として、とらえることが、できます。