

◆ ノイズ対策上の、基本であり、かつ対照的な性質を持つアナログ回路が、積分回路 と微分回路 です。
通常積分回路/微分回路と呼ばれているものには、それぞれ、幾つかの回路があります。それらの中には、真の積分/微分を実行する完全積分回路/完全微分回路と、不完全積分回路/不完全微分回路と呼ばれている、真の積分/微分とは異なる特性を有する回路とがあります。
◆ また、積分回路/微分回路には、アクティブ回路で構成されるものと、パッシブ回路で構成されるものの両方があります。パッシブ回路では、完全積分/完全微分を実現することはできません。全て不完全回路です。
積分回路と微分回路は、周波数特性を持っています。周波数特性を持たせるためには、周波数特性を有する素子を使用する必要があります。周波数特性を有する基本素子には、コンデンサとインダクタとがあります。
この講座では、積分と微分については、回路的な解説に止めてあります。さらに詳細は、別の講座「自動制御」の3.1.3.(1)、3.1.3.(5)を参照してください。
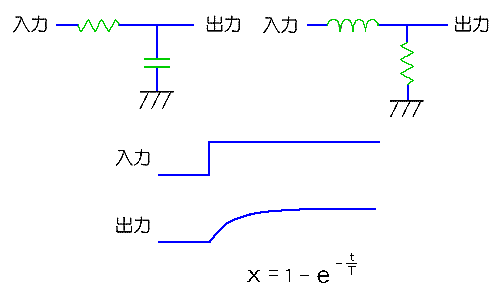
◆ パッシブの不完全積分回路 を、図.1に示します。図から分かるように、同じ特性を持つ回路を、R と C、および、L と R の組み合わせで、2 通り作ることができます。
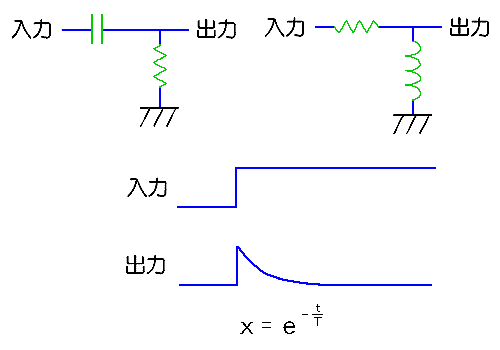
◆ 不完全微分回路 を、図.2 に示します。これも、2 通りあります。
◆ 図.1、図.2 は、コンデンサを使用した回路と、インダクタを使用した回路の両方を示しました。どちらを使用しても、作ることができます。しかし、一般に、コンデンサと、インダクタとを比較すると、コンデンサの方が、寸法が小さく、価格が安く、かつ、理想特性に近いものを、入手しやすいという、傾向があります。したがって、他に理由が無ければ、コンデンサを使用する方がベターです。この理由から、以降は、原則としてコンデンサ使用の場合のみを示します。
図.1、図.2 から、推定されるように、この 2 通りは、直列と並列との素子を交換し、同時に、コンデンサとインダクタとを取り替えると、特性が等しいものを作ることができます。
不完全積分回路/不完全微分回路と言う言葉があると言うことは、完全積分回路/完全微分回路が存在するはずです。しかし、完全積分回路/完全微分回路は、パッシブ回路では作ることができません。アクティブ回路で構成します。
◆ 不完全積分回路/不完全微分回路の言葉は、歴史的な過程から生まれたものと思われます。すなわち、増幅器が得られ無かった時代には、アクティブ回路で、真の積分回路/真の微分回路を作ることができなかったので、やむを得ず、代わり不完全積分回路/不完全微分回路を使用したのでしょう。
しかし、不完全積分回路/不完全微分回路は、真の積分回路/真の微分回路とは、異なる特性を持っています。そして、真の積分回路/真の微分回路と、特性が異なるが故に、有用な用途が存在します。代用品ではありません。
◆ 不完全積分回路/不完全微分回路のことを、単に積分回路/微分回路と、呼ぶことがあります。不完全積分回路/不完全微分回路は、真の積分回路/真の微分回路とは、特性が異なります。単に積分回路/微分回路と呼んだのでは、どちらであるのか、はっきり分かりません。
異なった内容のものを、同じ言葉で呼ぶことは、混乱と誤解の元になります。この講座では、以降、区別を明確にするために、完全積分回路/完全微分回路および、不完全積分回路/不完全微分回路と、フルネームで、呼ぶことにします。
図.1、図.2のコンデンサ使用の回路は、ディジタル回路と呼ばれている回路の中でも、ディジタル IC と共に、その補助として、しばしば使用されています。すなわち、非常にポピュラーな回路です。
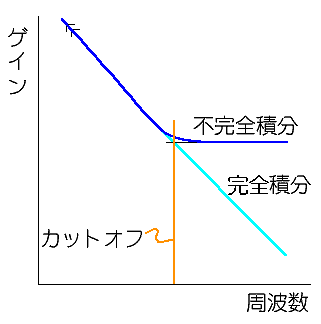
◆ 不完全積分回路は、ローパスフィルタの1種で、1次フィルタと呼ばれるフィルタと、同じ回路です。
不完全積分回路は、ノイズフィルタとして、アナログ回路、ディジタル回路を問わず、広く使用されています。時定数 T は、抵抗を R、キャパシタンスを C とすれば、T = RC です。カットオフ周波数 fc は、fc = 1/(2πRC) です。
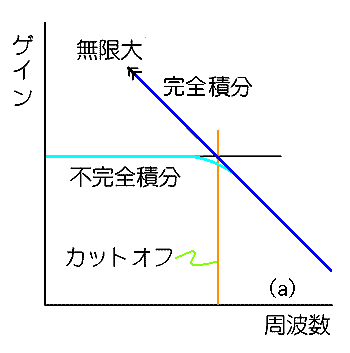
不完全積分回路の周波数特性を、図.3 に示します。
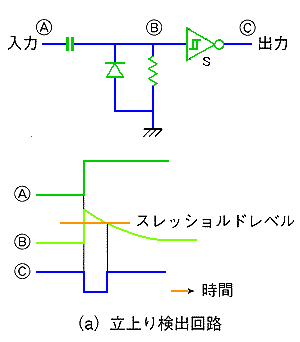
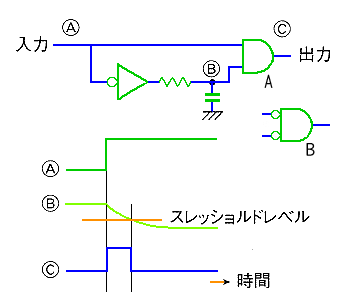
◆ 不完全積分回路は、アナログ回路です。しかし、不完全積分回路は、ディジタル回路中で、一定のディレイを作る、ディレイ回路 として利用されています。純粋にディジタル回路で作るよりも、簡単/安価/省スペースだからです(図.4)。ただし、この回路の時間精度は低いので、概略で差し支えないときしか使えません。図で、バッファ s は、シュミットトリガです。
◆ 精度を要する用途で、時間が短い場合(とくにnsオーダー)は、ディレイライン と呼ばれる製品を使用します。ディレイラインの素子は、ディレイ時間が固定ですが、タップ付きのものも、あります。
長いディレイには、モノマルチバイブレータまたはタイマーIC (一定時間を作る IC)を使用します。また、長い時間には、むしろディジタルタイマ を使用することが多くなっています。ディジタルタイマは、カウンタです。クロック信号を、一定数カウントすることによって、一定時間を作ります。
マイコンを使用していれば、ソフトウェアで、タイマーを作り、ソフトウェアタイマを、使用することができます。また、マイコンの周辺回路として、ソフトウェアで設定可能な、ディジタルタイマがあり、これを利用することも、できます。
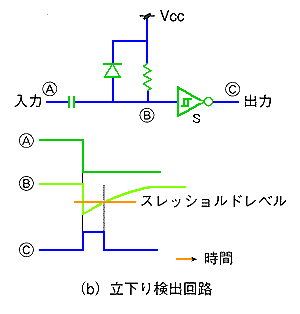
◆ 不完全微分回路は、ディジタル信号の、立ち上がり/立下りの検出に使用されます(図.5)。バッファ s は、シュミットトリガです。立ち上がり/立下り検出とは、図のように、パルスの立ち上がり、または立下りのところに、細いパルスを作る回路です。このパルスは各種の用途に利用されます。
◆ 完全微分回路は、パッシブ回路では作ることができませんが、後述するように、アクティブ回路なら作ることができます。
ただし、完全微分回路は、作ることは可能ですが、ノイズに極めて弱く、実用することは、不可能です。代わりに不完全微分回路を使用する必要があります(図.6)。
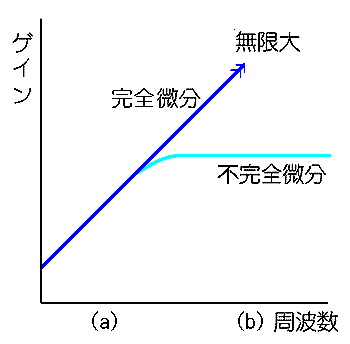
◆ 完全微分回路は、高い周波数において、ゲインが無限大になります。ノイズは、一般に信号より高い周波数です。このため完全微分回路は、ノイズ増幅器になってしまい、信号がノイズに埋もれてしまいます。
不完全微分回路は、高い周波数帯域において、ゲインが頭打ちになります。周波数特性の形は、1次フィルタ(不完全積分回路)と対称で、ハイパスフィルタです。不完全積分回路と同様に、時定数、カットオフ周波数が定義されます。
不完全微分回路では、ゲインが頭打ちになるという特性から、不完全微分回路は、完全微分回路の欠点を緩和します。すなわち、微分において、不完全微分回路を使用するのは、やむを得ないからではなく、ノイズ対策上必要なことなのです。
◆ 不完全微分回路を、ハイパスフィルタとしてではなく、微分特性を実現する回路として使用するときは、信号の周波数帯域において微分特性を持ち、それより高い周波数において頭打ちになるようにカットオフ周波数を設定します。すなわち、信号の周波数帯域が、図.6 の(a)になるようにして使用します。逆に、同じ回路を、ハイパスフィルタとして使用するときは、信号の周波数帯域が、図.6の(b)になるように使います。このように、特性曲線のどの部分を利用するかによって、用途が変わります。
不完全微分回路は、完全微分回路の欠点を緩和しますが、積極的に減らすのではありません。さらに積極的にノイズの影響を減らすためには、不完全積分回路を併用(直列接続)して、高周波のノイズを、減衰させます(図.7)。図のように、低周波、高周波共に減衰しているフィルタは、バンドパスフィルタです。
◆ 立ち上がり検出回路は、不完全積分回路を使用することによっても、作ることができます(図.8)。なお、図の A を B に変更することによって、立下り検出回路になります。
◆ この回路は、下記の理由によって、図.5の回路よりも優れているとして、文献に紹介されている回路です。次の内容です。
「微分回路はノイズに弱い。積分回路はノイズに強い。この理由から、図.5の回路よりも図.8の回路を使用すべきである」。
しかし、この解説は間違いです。一般論として、積分が、微分よりもノイズに強いと言うことは、嘘ではありません。ただし、それは、一般論であって、全ての場合に当てはまるわけでは、ありません。
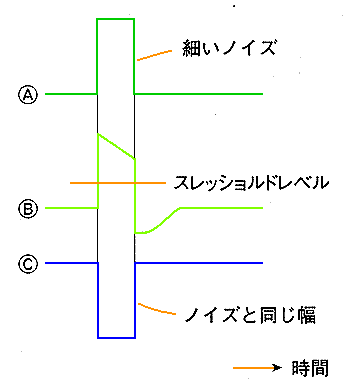
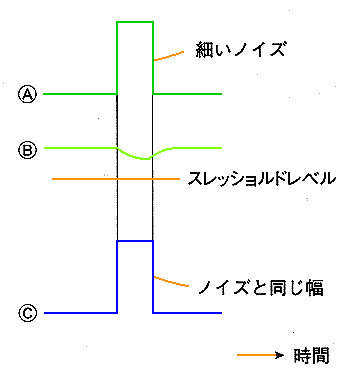
図を比較すれば分かるように、その応答波形は、ほとんど変わりません。したがって、ノイズに対する強さも、大差が、ある筈はありません。図.9は、このことを検証するために、細いパルス状のノイズに対する応答を、比較したものです。細部の応答は、若干異なりますが、大きな違いはありません。応答波形が、大体同じと言うことは、ノイズに対する強さが、大体同じと言うことです。先の文献は、微分はノイズに弱い、積分はノイズに強い、という思い込みから、実際の応答を調べないで、結論を出したものと考えられます。
[図.9] ノイズに対する応答の比較
(a) 図.5の回路
(b) 図.8の回路
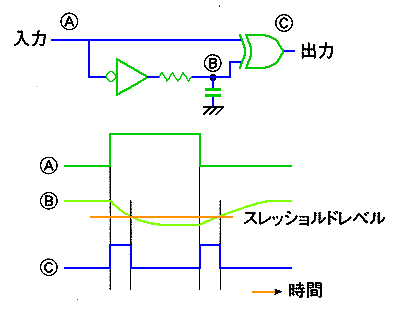
◆ 立ち上がり/立下りの両方を検出する回路もあります。この回路は、不完全積分回路の応用回路です(図.10)。
◆ モノマルチバイブレータ (ワンショット )の IC は、立ち上がり検出や、一定時間幅のパルスを作るなど、各種の用途があり、以前はよく使用された IC です(図.11)。しかし、ノイズに弱いので、過去の遺物と考えた方がよいでしょう。代わりに、ディジタルタイマを使用します。しかし、モノマルチバイブレータは、ノイズ対策の立て方の、良い見本ですから、その意味で、解説します。
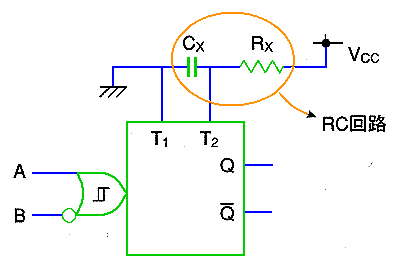
◆ 抵抗 Rx とコンデンサ Cx とで、不完全積分回路を構成し、これによってディレイを作っています。この部分が、ハイインピーダンスになることが多く、このため、ノイズに弱いのです1.(3-E-b)。
この IC は、ディジタル IC に属しています。このため、ディジタル回路の中で使用されます。周囲にディジタル信号線が走っています。ディジタル信号は、アナログにとって強力なノイズ源です。
ノイズ対策として、RC 部分の配線を最短とし、かつ、この付近に他の信号線を近づけないようにする必要があります。この RC 回路のプリントパターンのところに、他のディジタル信号のパターンが走っていたために、誤動作した実例があります。
◆ フィルタは、非常にシャープなカットオフ特性が要求される場合があります。パッシブフィルタでは十分シャープなフィルタを作ることができません。アクティブフィルタで対応する必要があります。
しかし、ノイズ対策用のフィルタは、特殊な用途(アンチエリアスフィルタ)を除いては、一般に、ゆるい特性のもので十分です。したがって、パッシブフィルタが多く使用されます。ノイズは、通常、信号よりも高周波です。ローパスフィルタ(不完全積分回路)を使用します。
ノイズ対策用にアクティブフィルタを使用する場合には、後述する理由によって、パッシブフィルタを併用する必要があります。
◆ 信号のレベルが低く、または高精度が要求されるときは、部品が出すノイズが問題になります(15.(2-A))。部品が出すノイズは、信号の周波数帯域の平方根に比例するものが多いので、信号の周波数帯域を狭くすることによって、ノイズを減らすころができます。
交流増幅では、直流をカットします。この直流カットのためのコンデンサは、ハイパスフィルタを構成します。これと高周波のイズカット用のローパスフィルタとを組み合わせることによって、バンドパスフィルタになります(図.12)。
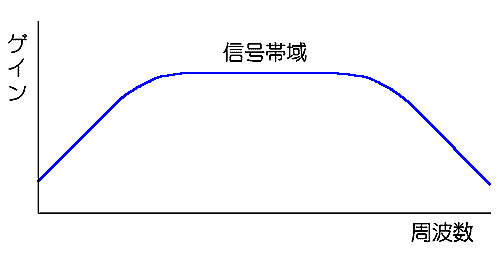
◆ バンドパスということでは、図.7と同じです。ただし、使い方が異なります。図.7の用途では、欲しい特性は、微分領域です。微分領域より高周波の周波数帯域は、不要な帯域ですから、できるだけ、はやく減衰して欲しいわけです。したがって、フラットな特性の部分が無く、高周波は、直ちに減衰させます。
それに対して、交流増幅器では、必要な信号周波数帯域が、フラットな特性を持っていなければなりません。ただし、ノイズ対策の立場からは、帯域幅が、必要にして十分であることが望ましく、帯域が、広すぎることは、ノイズを大きくします。大は小を兼ねません。
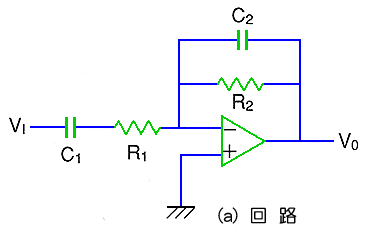
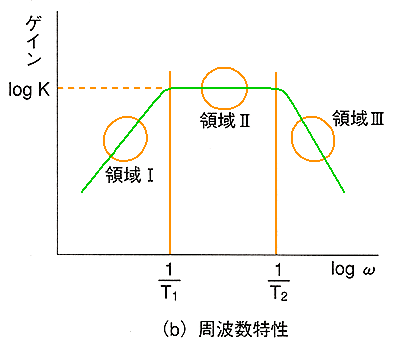
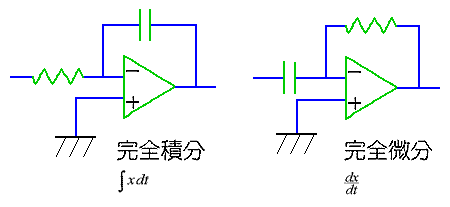
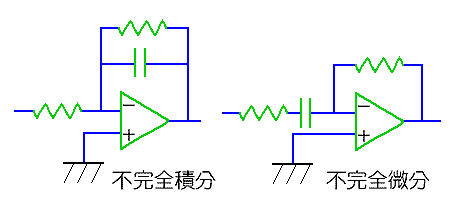
◆ さきに16.(2-A)で示したように、パッシブ回路では、完全積分回路/完全微分回路を作ることはできません。完全積分回路/完全微分回路を作るためには、アクティブ回路が必要です。完全積分回路/完全微分回路を図.13 に、その特性を図.14 に示します。
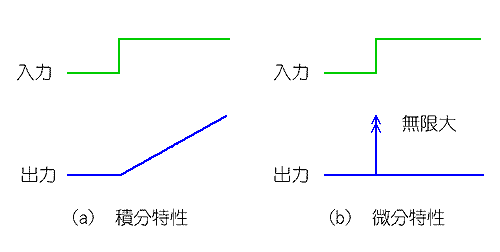
◆ しかし、完全微分回路は実用になりません(16.(2-C))。したがって、アクティブ回路においても、不完全微分回路を使用しなければ、なりません。。
完全積分回路は、実用があります。しかし、アクティブ回路においても、不完全積分回路を使用することが必要な場合があります。アクティブの不完全積分回路 /不完全微分回路 の 1 例を図.15 に示します。
◆ ある範囲の特性を持つ、フィルタは、パッシブ、アクティブどちらでも作ることが可能です。しかし、アクティブフィルタでなければ、作ることができない、特性のものもあります。とくに、より特性の優れたフィルタは、アクティブでなければ作ることができません。
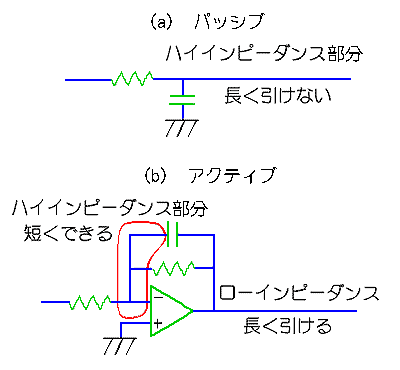
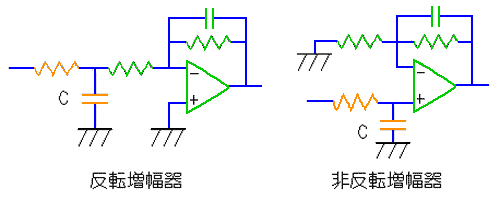
パッシブでも、アクティブでも、同じ特性のものが得られる場合は、当然パッシブフィルタの方が、簡単で安価です。しかし、ノイズ対策の立場から、アクティブフィルタを使用した方が、良い場合があります(図.16)。ただし、パッシブフィルタであっても、フィルタの下流にバッファまたは非反転増幅器を挿入すれば、耐ノイズ性の点では、アクティブフィルタと、ほぼ同等になります。
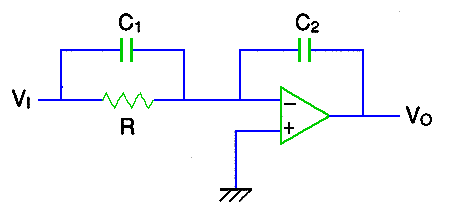
◆ アクティブの不完全積分回路は、上記に説明した、パッシブフィルタと同じ特性を持つものの他に、別の特性を持つものを作ることができます(図.17)。
[図.17] 別の特性を持つ不完全積分回路
(a) 回 路
(b) 周波数特性
◆ この特性は、低周波で完全、高周波で不完全特性を持ちます。一般の電子回路では、あまり使用されませんが、この特性は、自動制御のコントローラで、PI動作の名で実用されています。
◆ 完全積分回路は、通常は、問題なく使用することができます。しかし、不完全微分回路が、完全微分回路の代わりに利用できたのと同様に、不完全積分回路も完全積分回路の代わりに使用することができます。すなわち、図.3 における(a)の周波数帯域は、不完全積分回路であっても、完全積分回路の特性と同じですから、どちらを使用しても同じです。
ただし、積極的に不完全積分回路を利用した方が良い場合もあります。
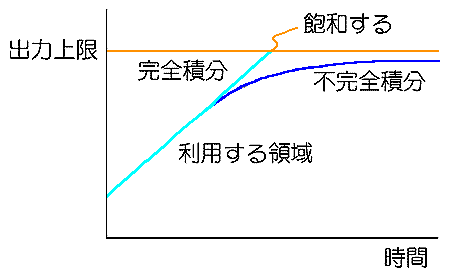
アクティブの完全積分回路は、入力がゼロで無い限り、その値を積分し続けるために、出力が飽和します。すなわち電源電圧で決まる最大または最小値にへばりつきます。
オペアンプの機種によっては、飽和が起こると、正常動作に回復するのに、時間を要するものがあります。これが問題になる場合には、不完全積分を使用すると、飽和を避けることができる場合があります(図.18)。ただし、不完全積分回路を使用しても、条件によっては、飽和が起こります。実際に使用する回路で、飽和が起こらない条件を求める必要があります。
◆ ノイズ対策として、ノイズをフィルタする目的で使用するときは、アクティブフィルタにも制約があります。一般に、全ての素子は、回路図に無い回路で、理想特性から隔たります。通常、信号の周波数帯域の範囲で、ほぼ理想特性を満足するように、素子を選定します。
ところがノイズは、信号周波数よりも高周波です。抵抗やコンデンサを、ノイズ周波数で効果があるように選んでも、オペアンプの周波数帯域がこれをカバーしないと、これによってアクティブフィルタが、高周波のノイズ周波数では機能しなくなります。すなわち、ノイズに対しては効かなくなってしまいます。
◆ オペアンプの機種を、ノイズ周波数をカバーするように選択することも、考えられます。しかし、信号に対して所定の特性を満たし、かつノイズ周波数においても動作するオペアンプを得ることは困難です。得られたとしても高価です。
より実用的なのは、パッシブフィルタを併用して、高い周波数のノイズに対しては、パッシブフィルタで対応することです(図.19)。図の C が、パッシブフィルタです。
◆ ノイズ対策用フィルタは、通常シャープな特性を必要としません。しかし、アナログ/ディジタル変換におけるノイズフィルタ(アンチエリアスフィルタ)の場合には、シャープな特性を必要とします。
このためには、アクティブフィルタが必要です。かつ、高次フィルタ と呼ばれるフィルタを使用します。フィルタには、次数と呼ばれるものがあります。高次フィルタは、2次以上のフィルタの総称です。フィルタの次数が高いほど、シャープな特性を実現することができます(図.20)。
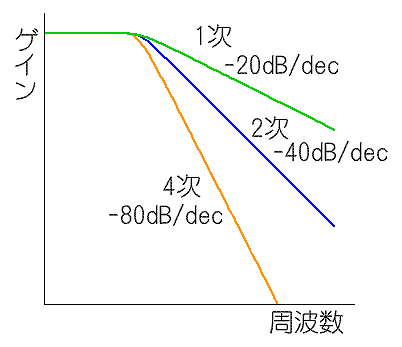
◆ 図で、-20dB/dec は、周波数が 1dec(10倍)につき -20dB 変化することを示します。次数に比例して特性がシャープになっていることが分かります。
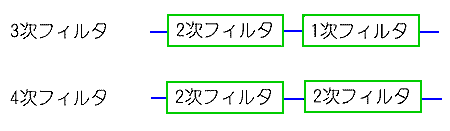
2 次フィルタ が高次フィルタの基本です。2 次以上のフィルタは、通常、2 次および 1 次フィルタを組み合わせて作ります(図.21)。
◆ 以下、2 次のローパスフィルタについて説明します。図.22は、2 次ローパスフィルタ回路の 1 例です。
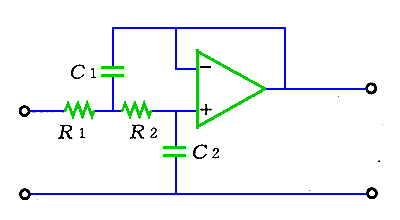
◆ 1 次フィルタは、抵抗とコンデンサが、各 1 個で構成されます。2 次フィルタは、抵抗とコンデンサが 2 組あります。一般に n 次フィルタは、抵抗とコンデンサが、n 組になります。
この 2 次フィルタのカットオフ周波数 fc は、
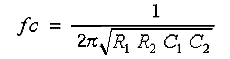
です。また、Q (QUALITY FACTOR)が、次式で与えられます。
1 次フィルタでは、波形は一定でしたが、2 次フィルタでは、波形が変わります。波形を決めるのが Q の値です。Q と周波数特性との関係を図.23に示します。
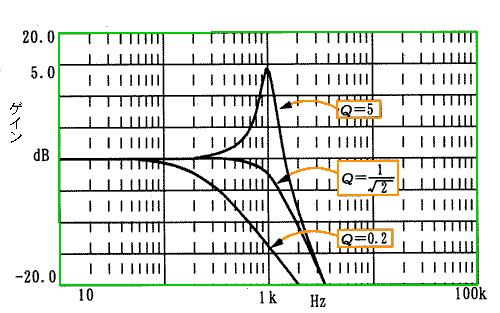
◆ 図は、カットオフ周波数が 1 kHzの場合を示します。周波数が十分低い通過域と、周波数が十分高い阻止域は、Q による特性の違いはありませんが、カットオフ周波数の付近の特性は、Q に大きく支配されます。
Q が小さいと、カットオフ特性がゆるくなります。これに対して、Q が大きいと、ゲインにピークが発生します。これは、共振 現象です。一般的なローパスフィルタでは、共振現象は好ましくありません。Q=1/√2 のときをクリティカルダンピング (臨界制動 )といい、ゲインにピークが発生しない条件で、もっともシャープなフィルタ特性を示します。
◆ パッシブフィルタでは、クリティカルダンピングの条件に、ある程度までは近付けることができますが、クリティカルダンピングよりも、ゆるい特性のものしか作ることができません。