◆ 通常、3 次以上の遅れを一括して多次遅れ と呼んでいます。多次遅れでは、次数が異なれば、定量的性質はもちろん異なりますが、定性的には似たような特性になります。
n 次遅れ は、伝達関数の分母が s の n 次式になっています。
基本的には、2 次遅れと同様に、振動的な解と、非振動的な解があります。振動的な解のときは、特性方程式の根に、複素根が存在します。非振動的な解は、特性方程式の根がすべて実根です。
n 次遅れの周波数応答は、ゲインの高周波領域の減衰が 20×n dB/dec になります。高周波領域での位相は 90×n °です。振動的な解になるときは、ゲインにピークが現われます。
非振動条件では、2 次遅れと同様に、n 次遅れは n 個の 1 次遅れのカスケード接続になります。
◆ 3 次遅れ の標準的な形を示します。
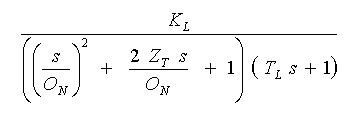・・・ (3-1-16)
この式は、3 次遅れで示される、多くの制御要素に適用できますが、この形で表されない 3 次遅れもあります。3 次遅れの応答を図 3-1-25 〜図 3-1-26 に示します。
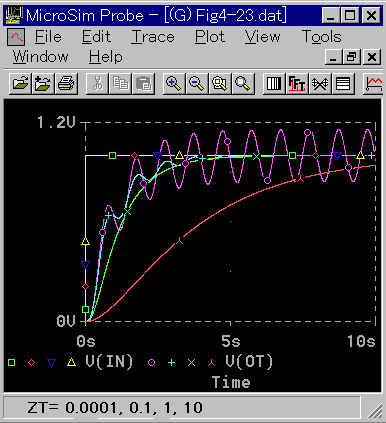
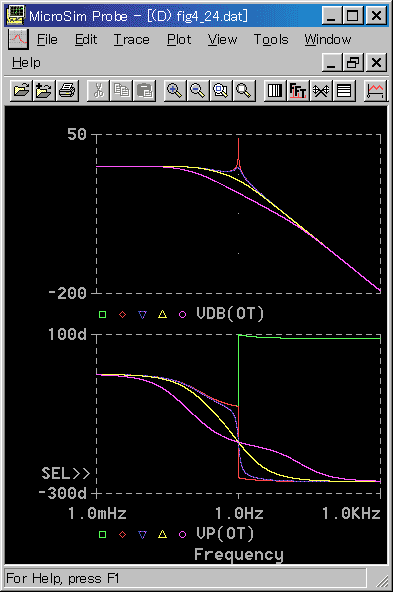
◆ n 次遅れの周波数応答の位相は、高周波領域では、-90×ｎ°の筈です。ところが図 3-1-26では、ZT = 0 のとき、周波数応答の高周波領域の位は -270°にならないで、逆にプラス90°になっています。エラーメッセージは出ませんが、明らかにエラーが発生しています。
ちょうど、360°ずれています。正弦波形は、位相が 360×n °ずれたものは、同じものです。ZT ≒ 0 のときは、カットオフ周波数(1kHz)のところで、位相が跳躍しています。
このため PSPICE が間違えたのでしょう。間違えたことに気付かなかったので、エラーメッセージも出なかったのでしょう。
[ケース・スタディ 3-1-3]
★ fg3-1-25.cir 〜 fg3-1-26.cir では ZT だけを変えています。他のパラメータも変えて、ケース・スタディしてみてください。
★ なお、シミュレーションに興味がある読者は、次のことも試みてください。
図 3-1-25 のステップ応答では ZT=0 が入っていません。ZT=0 を実行してください。
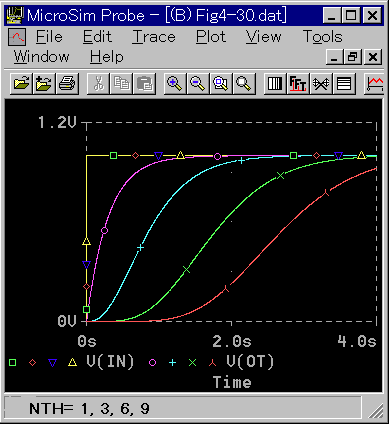
◆ 2 次遅れ以上のステップ応答では、最初の立ち上がりが水平方向から始まります。したがって、波形には変曲点があります。1 次遅れでは、最初の立ち上がり時の傾斜が最も急で、変曲点はありません (図 3-1-27)。
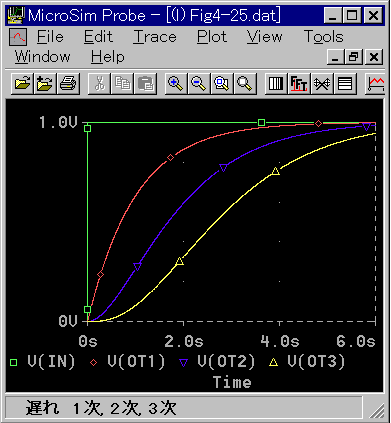
◆ このように、ステップ応答は、1 次遅れだけは、波形に大きな特徴がありますが、2 次遅れ以上について、それが何次遅れであるかを区別できるような、大きな特徴はありません。
[注] 図 3-1-19 および図 3-1-21 では、2 次遅れの最初の立ち上がりが、水平ではなく、もっと急のように見えます。しかし横軸を拡大して観測すれば、水平から立ちあがっていることが分かります(PROBE 画面のスケール変更は2.1.6.(2-E-a) 参照)。
◆ 高次遅れのステップ応答においては、振動的な解の中には、振幅が発散 する場合があります (図 3-1-28)。
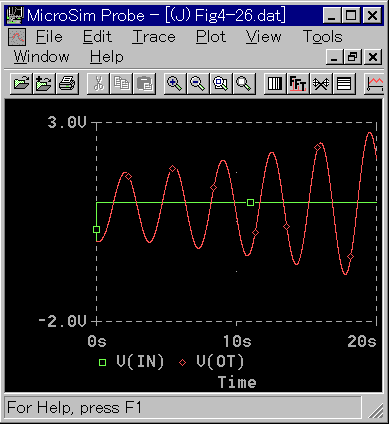
◆ 発散するときは振幅は無限大になります。すなわち不安定です。
2 次遅れでは最も不安定な場合でも持続振動であり、発散することはありません。
[注] 式 3-1-16 では発散する解は得られません。図 3-1-28 は、別のモデルを使用しています。
フィードバック制御が実用化さた初期には、自動制御によって安定させようと思ったにも関わらず、逆に不安定になってしまうことがあり、その原因がわからないので、大きな問題になりました。
フィードバック制御理論の始まりは、この問題を解決するためでした。それが発展して、現在の制御理論になったのです。
[ケース・スタディ 3-1-4]
★ このケース・スタディは、fg3_1_28.cir が対象です。シミュレーション自体に興味がある読者が実施してください。
★ PSPICE では、伝達関数それ自体が発散条件であると、警告が出て、解が異常になります。このモデルでは (KP = 9) のときが該当します。したがって、発散する解を直接シミュレーションすることはできません。
★ しかし、モデルを変形して、フィードバック形にし、フィードバックを掛けない条件では非発散のモデルとすれば、発散する正常な解が得られます。ただし、計算の途中で、解の数値がシミュレーションの範囲を超えるときは、演算途中で打ち切られて、エラーになります。
★ 図 3-1-28 はフィードバック形を使用して、発散条件をシミュレートしています。回路ファイルには、オープンループ形のモデルも入れてあります。それを試してみてください。
非発散の条件 (KP = 7) では、オープンループ形でも正常な解が得られます。
★ この講座では周波数応答は示してありませんが、これも試してください。周波数応答では、(3-A) に示した、位相の 360°の跳躍があります。
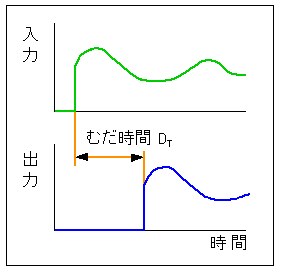
◆ むだ時間 要素も、遅れの一種ですが、n 次遅れとは違った特性を持っています。時間領域では、入力を x(t) 出力を y(t) とすると、むだ時間は、
・・・・ (3-1-17)
となります (図 3-1-29)。
◆ また、むだ時間の伝達関数は
・・・・・ (3-1-18)
です。この伝達関数は、式(3-1-17) をラプラス変換することによって得られます。
むだ時間のステップ応答を図 3-1-30に、周波数応答を図 3-1-31 に示します。
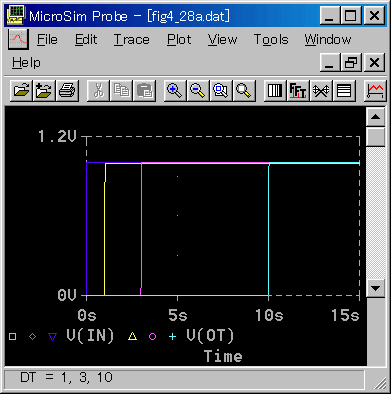
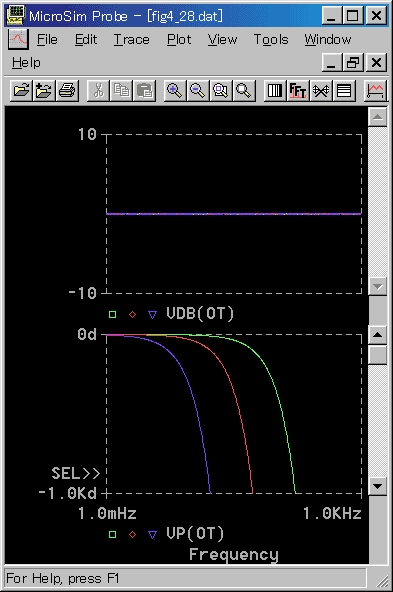
◆ ゲインは全周波数帯域で 0 dB です。位相遅れは、周波数の増加とともに急速に増大します。
高次遅れは、むだ時間ではありませんが、等価的にむだ時間が発生します。とくに、時定数が等しい 1 次遅れを多数直列に接続したとき、大きな等価むだ時間になります (図 3-1-32)。
◆ むだ時間の代表例は、コンベア・システムです (図 3-1-33)。
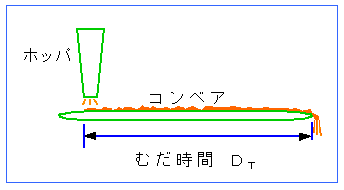
コンベア上の粉体流量の、ホッパの直下からコンベアの終端までの間の応答は、むだ時間となります。コンベア速度が一定であれば、むだ時間は一定です。
◆ PID 制御には、積分と微分とを含んでいます。ここでは先ず、積分と微分 単体の特性について解説します。
◆ 積分 は微分の逆演算です。ラプラス変換において、微分 d/dt は s に変換されました(3.1.1.(4))。積分 ∫dt は 1 / sに変換されます。すなわち、ラプラス変換領域では、微分と積分は逆数の関係にあります。
積分要素のステップ応答と周波数応答を、図 3-1-34 〜図 3-1-35 に示します。
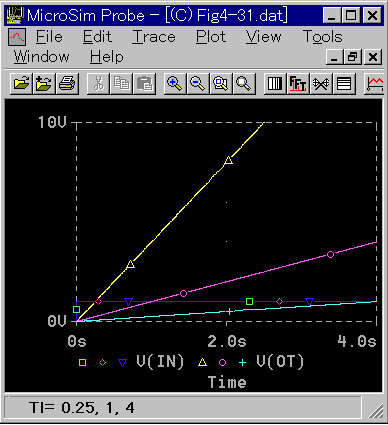
◆ 積分ですから、一定値の入力に対する出力は、一定速度になります。
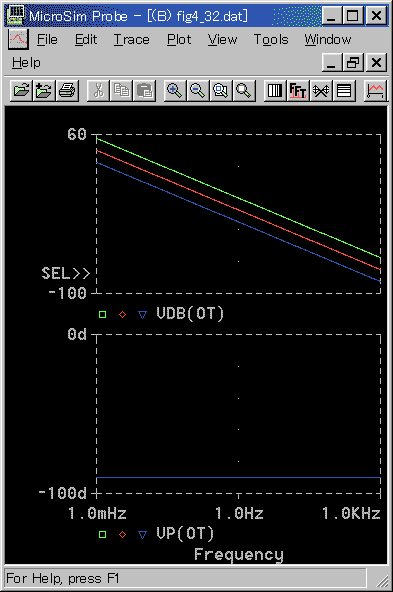
◆ 周波数応答のゲインは -20 dB/dec の直線になります。したがって周波数 f → 0 のときゲインは ∞ です。位相は -90°で一定です。
◆ 微分 d/dt のラプラス変換は、すでに示したように s です。微分は、その定義から、真のステップ応答は値が無限大で幅がゼロのパルスになります。
PSPICE のステップ入力は、真のステップではなく、有限の時間で立ち上がります。
しかし、それでも伝達関数 s のステップ応答を求めようとすると警告が出て、演算のステップ幅が異常に短くなり、その結果演算時間が長くなり、しかも波形が異常になります。
周波数応答は、正常な解が求まります (図 3-1-36)。
ゲインは 20 dB/dec の直線で、位相は 90°で一定です。
◆ 以上の、シミュレーション上の問題とは別に、微分動作には、実用上の問題があります。
微分は、図 3-1-36 からも分かるように、入力の周波数が高いときゲインが非常に高くなります (周波数が ∞ のときゲインは ∞)。
PSPICE のような、シミュレーション上の信号はきれいですが、現実の信号には必ずノイズが存在します。ノイズの周波数は、一般に信号の周波数よりも高く、しかも周波数が高いほどノイズが多くなる傾向があります。
微分を行なう前の信号の S / N (信号とノイズとの比) が良好であっても、微分要素の出力は、ノイズが増幅される結果、本来の信号が、ノイズに埋もれてしまいます。
これを防止するためには、微分要素を使用するときは、高周波のノイズをカットするローパス・フィルタを併用する必要があります。
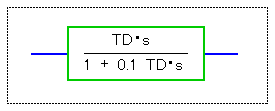
◆ 本来は、そのシステムのS/Nを調べて、それにマッチした最適なフィルタを使用するのが、良い筈です。しかし実用上は、微分時間の 1 / 10 の時定数をもつ 1次遅れ要素(フィルタ)と組み合わせれば、十分です (図 3-1-37)。
◆ これを使用すれば、ほとんどの場合ノイズの問題はなくなり、実用上、十分な微分効果が得られます。
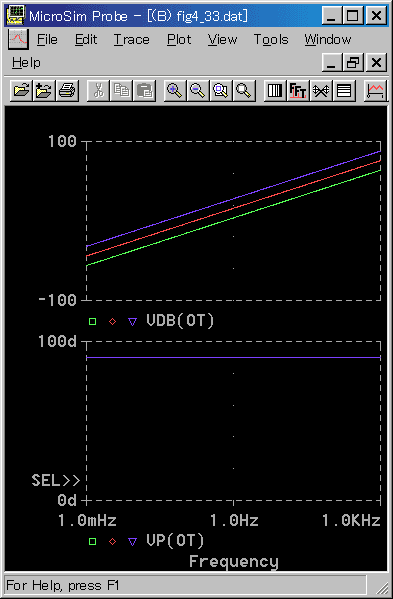
この、実用微分要素 の特性を、図 3-1-38 〜図 3-1-39 に示します。
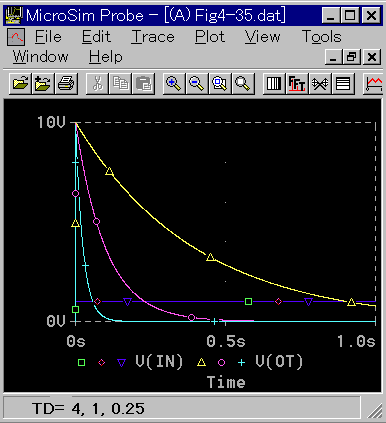
◆ ステップ応答は、ピーク高さが入力ステップの 10倍の指数関数になります。
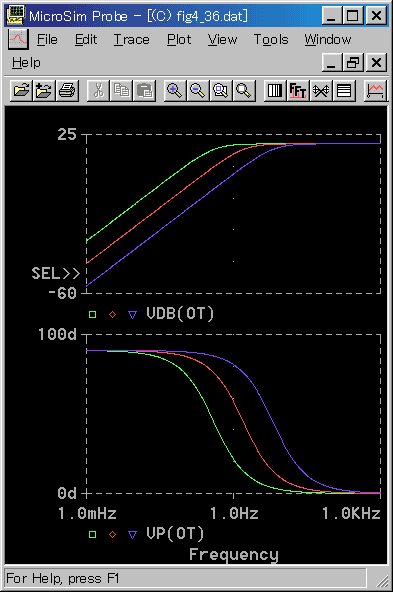
◆ 周波数応答は、低周波領域では微分特性を示します。高周波領域ではゲインが 20 dB で頭打ちになり、ノイズを過大に増幅することを防いでいます。
微分特性の特徴は、位相が 90°進むことにあります。高周波ではその特徴は失われています。したがって、低周波では微分特性が、そのまま発揮されますが、高周波では、微分特性が失われます。
[注] 2.2.5.(2-A) リスト 2-2-4 に示した PID の制御演算式はRC回路ですが、微分動作に 1 次フィルタが付加してありました。このフィルタは上記の目的だったのです。
★ 実用微分要素の 1次遅れの時定数は、微分時間の 1 / 10 です。FIG4_35.CIR と FIG4_36.CIR において、この比
KD を変えて、特性の変化を調べてください。
★ なお、シミュレーションに興味がある読者は、上記の比を大幅に変えて、1 次遅れがない状態を含めてケーススタディすると良いでしょう。
