1. 自動制御とは
◆ 自動制御 は、制御のやり方によってシーケンス制御とフィードバック制御に大別されます。
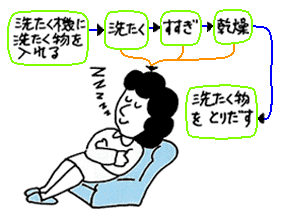シーケンス制御 は、たとえば全自動洗濯機で、一連の洗濯の操作を自動的に行うような制御です。
フィードバック制御 は、たとえばエアコンで、室温を一定にするような制御です。
シーケンス制御は、論理演算が主体の制御であり、もともとディジタルの制御です。これに対して、フィードバック制御は、従来は、ほとんどがアナログ・コントローラを使用していました。
しかし、今やディジタルの時代です。フィードバック制御もディジタル化が進んでいます。ディジタル化によって、より容易かつ安価に、しかも高度な制御が可能です。
◆ フィードバック制御は、あらゆる分野で利用されています。その中で、代表的な応用分野として、機械産業を対象とした、メカニカル制御 と、装置産業を対象とした、プロセス制御 があります。
◆ 図 1-1 に、温度制御 を例にとって、フィードバック制御系の構成を示します。
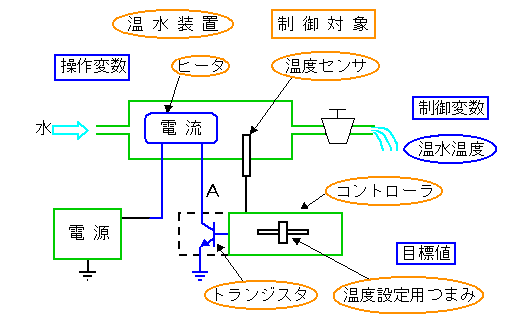
◆ 「制御対象」 (この例では温水装置) の、制御したい量 (この例では温度) を「制御変数」、制御するために操作する量 (この例ではヒーター電流)を「操作変数」と呼びます。「センサ」によって制御変数の値を検出しています。
制御変数の望ましい値を「目標値 (設定値) 」と呼びます。図の例では、「温度設定用つまみ」によって手動で目標値を変更できます。
そして、制御を実行する装置が「コントローラ (調節計または調節器) 」です。
◆ 図 1-2 は、図 1-1をハードウェア的に抽象化した図です。
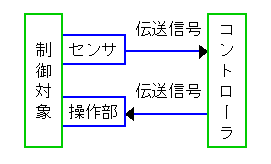
◆ センサは、制御変数を検出する部分です。
「操作部」は、コントローラからの出力を受けて、制御対象に働きかける部分です。
操作部は、自動制御のための要素ですが、むしろ制御対象に含まれると考えられます。コントローラは、情報 (信号) の処理を行います。操作部は、情報(信号) をパワーに変換する部分です。
図 1-1 の例では、電流を変化させる機構 (トランジスタ) によって電力を制御し、ヒータによって電力を熱に変えています。この例では、操作部の働きは情報をパワーに変換すること、そのものです。
◆ 機械系の制御では、多くの場合、操作部は、信号を物の動きに変換します。物を動かすためには、パワーが必要です。物を動かすための操作部を、アクチュエータ といいます。
プロセス系の制御では、操作部は、多くがバルブ の開度を調節するによって、プロセスの各流量 を変化させます(図 1-3)。バルブの開閉も、物の動きに帰着します。
◆ 操作変数は、制御変数の値を十分に変化させる能力を、持っていなければなりません。これは、当然のことですが、うっかりすると、忘れることがあります。
◆ 図 1-1 を、信号の流れとして、抽象化して表したものが、図 1-4 です。このような図を「ブロック図 (ブロック ダイヤグラム)」と呼んでいます。
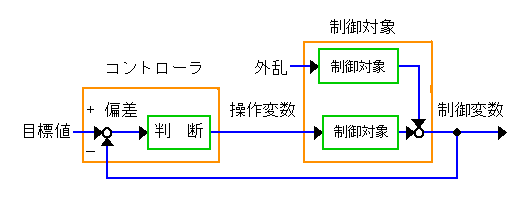
◆ 制御変数と目標値との差を「偏差」と言います。フィードバック制御の目的は、この偏差をゼロにすることです。
コントローラは、この偏差をゼロにするためには、操作変数の値をどのような値にすればよいかを、「判断」します。
判断するということは、人間で言えば、頭脳の働きを持っている、ということです。すなわち、コントローラは、手足の働きをする、単なる機械ではありません。
この判断のやり方には各種あります。判断のやり方によって、簡単なコントローラから、高度なコントローラまで、さまざまなものがあります。
判断の内容は演算なので、この部分は「制御演算」、「制御演算式」、「制御アルゴリズム」などと呼ばれています。
◆ ブロック図では、図 1-2のところに示した考え方から、操作部は制御対象に含まれるとして、明示されていません。図 1-2 と対比すると、図1-4 に示した操作変数の部分は、コントローラ出力であり、操作変数ではありません。
実際の物理的な流れは、コントローラ出力信号が操作部に入り、操作部で操作変数に変換されています。したがって、コントローラ出力信号と操作変数とは、1 対 1 に対応しています。
操作部の記載が省略されているブロック図においては、判断から制御対象にいたる信号は、コントローラ出力であり、また同時に操作変数をも表している、と考えることができます。
この意味で通常は、この部分を操作変数と呼んでいます。
◆ フィードバック制御系は、図から分かるように、信号が閉じて、ループを描いていることが、特徴です。このことから、フィードバック制御を、「クローズドループ制御」とも呼んでいます。
また、コントローラの数を数えるときに、1 台、2 台と呼ばないで、1 ループ 、2 ループという呼び方をすることがあります。
◆ 「外乱」は、制御変数の値を変化させ、制御を乱す要因です。図 1-1 の温度制御の例では、たとえば、水の流量を変化させることが、外乱です(図 1-5)。加熱量が同じで、水量を変化させれば、水温は変化します。
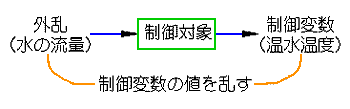
◆ 外乱がなければ、自動制御しなくても制御変数の値は変化しないで、一定に保たれるはずです。外乱が存在し、外乱によって制御変数の値が変化してしまうから、フィードバック制御が必要になるのです。
◆ 図 1-1 のような温度制御では、一般に目標値の値は一定です。自動制御しないと、外乱によって温度が変化してしまうのを、フィードバック制御によって、温度を一定に保ちます。このように、目標値が一定で、外乱によって制御変数の値が、変化してしまうことを防ぐ制御を、「定値制御」と呼んでいます。
定値制御において、外乱が発生したときに、制御無しの場合と、制御を行ったときとで、制御変数の変化が、どのように違うのか、その例を図 1-6 に示します。図の横軸は時間で、縦軸は各変数です。
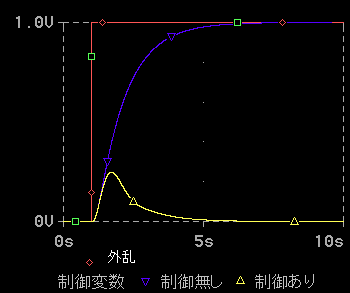
◆ この講座では、シミュレータ によって、シミュレーション を行っています。この、図 1-6 は、シミュレーション波形です(以降に示す波形もシミュレーション波形です)。赤は外乱で、ステップ状の外乱が入ったときの制御応答です。
フィードバック制御していないときは、青のように大きな偏差が発生します。しかし、フィードバック制御のおかげで、外乱が発生しても、黄色のように、制御変数の値は元の値に戻ります。
しかし、フィードバック制御を行っていても、図に示すような、一時的な偏差の発生を、避けることは、できません。
[注] この第 1 章では、シミュレーションによる波形は、結果だけを示します。つぎの 2.1.、2.2. 章で、シミュレータ、およびシミュレーションについて、解説します。第 3 章以降は、シミュレーションを含んだ、解説を行います。
◆ 目標値が、一定ではなく、目標値が時間と共に変化し、その目標値を追いかけて、制御変数を追随させる形の、制御もあります。これを「追値制御」と言います。目標値が変化する原因と、目標値変化が変化する波形には、さまざまなものがあります。
追値制御の例を、図 1-7 に示します。追値制御の場合でも、制御変数は、目標値に直ちに追尾することは、できません。図に示されているような「遅れ」が存在します。
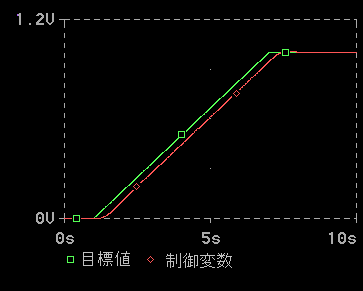
◆ 追値制御は機械系の制御で多く使われています。機械系における追値制御のことを「サーボ」とも呼んでいます。サーボとは召使の意味です。制御を、主人の指図どおりに働く、召使にたとえて、名付けられたものです。
召使の場合は、指図の内容は、「1 歩進め、右を向け」、といった指図ではありません。「部屋を掃除しろ」、と指図すれば、どのように掃除するかは、召使が判断して、実行してくれます。
◆ しかし、簡単なコントローラは、召使のように高度な判断は、してくれません。単純な判断しか、行いません。しかし、自動制御が、自主的に判断する機能を、持っているということは、単なる機械と、根本的に異なります。
◆ 定値制御においても、制御の開始時など必要に応じて目標値を変化させることがあります。
たとえば、図 1-1 の温度制御系においても、温水の温度を変更したい場合があります。このような場合には、一般に、目標値を図1-8 に示すようにステップ状に変化させます。
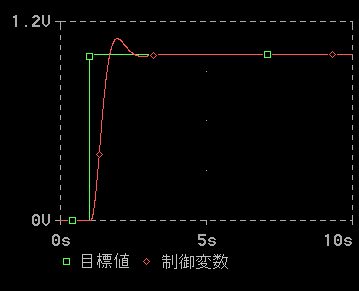
◆ これも、1種の追値ですが、通常は、このような、目標値のステップ状の変化に対しては、追値制御とは言いません。図 1.7 のように、目標値が、あるパターンで変化する場合を、追値制御と呼んでいます。
◆ 制御においては、図 1-6、図 1-7、図 1-8 に示したように、ある要素に信号が入力されたとき、その出力が、どのように変化して行くかという、時間的変化が問題になります。
入力の変化と、その変化に対応して出力が変化する様子を「応答」といいます。
特定の、典型的な入力波形を使って、応答を調べれば、対象の特性を、直感的に分かりやすく、表現することができます。最も単純で、直感性の高いのは、ステップ状の入力波形に対する応答です。これをステップ応答と言います。
図 1-6 は外乱入力に対する制御変数のステップ応答、図 1-8 は目標値変化に対する制御変数のステップ応答の例です。
◆ 図 1-7に示すような、一定速度の関数をランプ関数 といいます。ランプ関数入力に対する応答がランプ応答 です。
