◆ PID制御 の制御演算式は、次のようになります。
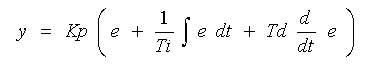・・・・ (1-2)
ここで、e は偏差、y は制御出力で、Kp、Ti、Td は定数です。制御演算式は、3 つの項から、成っています。
第 1 項 e は、偏差に比例する制御出力を、与えます。すなわ、ち比例制御の項(P動作)で、PID 制御の基本になる項です。
比例定数 Kp は、比例項の比例定数を意味します。比例ゲイン (略して単にゲイン) と呼びます。
式(1-2)では、Kp は 3 つの項全体に、かかっています。このようにする方が、実用上便利だからです。
◆ 第 2 項は、偏差 e の時間積分です。この項を「積分動作」と呼び、積分 (インテグラル) の頭文字を取って、I動作 とも呼びます。
この項の比例定数は 1/Ti で、Ti は時間の次元を持つので積分時間と言います。
第 3 項は偏差 e の時間微分です。「微分動作」と呼び、微分 (ディファレンシャル) の頭文字を取ってD動作 とも呼びます。
この項の比例定数は Td で、微分時間と言います。
積分動作と微分動作は、比例動作の、欠点を補うための、補助動作です。
[注]
一般に、PID動作の制御式は、式 1-2 のように、説明されています。
しかし、実際には、この式を若干変形したものが、多く使われています。定量的には、違いがありますが、定性的な動作は、同じと考えて、差し支えありません。
◆ P動作(比例制御)の効用はすでに1.4. (2) に示しましたが、さらに詳しく調べて見ます。図 1-28 は目標値変化に対する制御応答、図1-29 は外乱入力に対する制御応答です。
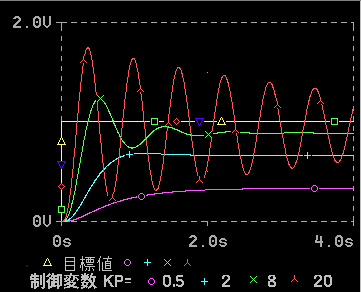
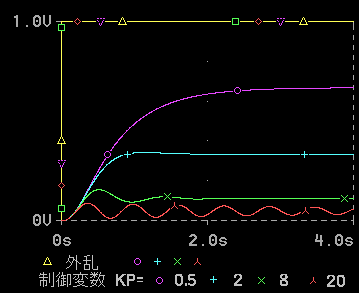
◆ 図 1-28、図 1-29 は、共に、比例ゲイン Kp をパラメータに取ってあります。どちらも、比例ゲイン Kp を大きくするほど、制御応答が速くなっていることが、分かります。
ただし、比例ゲイン Kp をさらに大きくする(図では、Kp=20）とハンチングが発生します。図は、減衰振動 の範囲ですが、Kp をさらに大きくすれば持続振動 となり、さらに Kp を増加すれば発散 (振幅が増大し、ついには無限大になる不安定な現象) します。
以上から、比例ゲインを上げるには、限界があることが、わかります。
◆ 図 1-28、図 1-29 どちらも、十分に時間が経過して、定常状態に達したときに、偏差がゼロにならないで、一定の値に落ち着いてしまう、現象があります。このように、定常的に残る偏差のことを、「オフセット」と呼びます。
オフセットは好ましくない現象です。オフセットの値も、比例ゲインを大きくするほど小さくなります(図 1-28、図 1-29 とも)。
オフセットの面からも、比例ゲイン Kp の値を大きくすることが望ましいわけです。しかし、上記の制約があります。
すなわち、P 動作では、オフセットをゼロにすることができません。
◆ フィードバック制御では、制御対象の特性によって、制御応答が大幅に違います。これまでのシミュレーション波形は、同じ制御対象を使用して、その他の条件の違いによる特性の変化を見てきたのです。
図 1-30 は、これまでとは異なった、制御対象に対して、図 1-28と同様に、P 動作の制御を行ったものです。
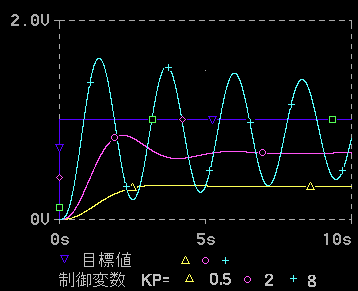
◆ 図 1-28と比べてみると、同じ比例ゲインでの制御応答が、より振動的です。 制御可能な、比例ゲインの大きさは、大幅に、抑えられてしまいます。したがって、制御応答も悪く、オフセットも、大きくなっています。
この例のように、制御応答は制御対象の特性によって大きく支配されます。したがって、制御実験を行うときは、下記の2種類の比較を行う必要があります。
(1) 同じ制御対象において、制御演算式や制御パラメータの違いによる、制御応答を比較する。
(2) 制御対象の特性の違いに対する、制御応答を比較する。
◆ 今後、各種の実験 (シミュレーション) を行います。
それらの実験において、制御対象の特性による違いを、検討する場合には、主に、次の2種類の制御対象を使用して、シミュレーションを行います。その制御対象の名前、を下記のように定めます。
●「標準N」の制御対象
比較的制御が容易な制御対象の代表として、使用します。これは、図 1-28 で使用した、制御対象です。
●「標準K」 の制御対象
比較的制御が難しい制御対象の代表として、使用します。これは、図 1-30 で使用した、制御対象です。
◆ 一方、制御成績の評価基準も、制御対象によって、異なります。たとえば、オフセットは、各制御対象ごとに、許容限界が与えられます。その制御対象において、許容される値以内であれば、仮にオフセットの絶対値が大きくても、その制御対象においては、合格であり、使用に耐えます(1.7参照)。
オフセットの値を、許容限界内に抑えることが、できない場合には、P 動作だけの制御で、は対応できません。次項で説明しますが、I 動作を導入する、必要があります。
◆ 積分動作(I 動作)は、オフセット をゼロにする能力を、もっています。したがって、P 動作の欠点を、補うことができます。I 動作を P 動作と組み合わせた、PI 動作 の制御演算式は、
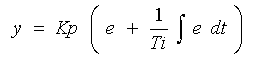・・・・ (1-3)
になります。ここで、Kp : 比例ゲイン、Ti : 積分時間です。
シミュレーションの結果を、図 1-31 (目標値変化)、および図 1-32 (外乱入力)に、示します。PI 動作の効果が、よく現れるように、制御対象は、「標準K」を使用しています。
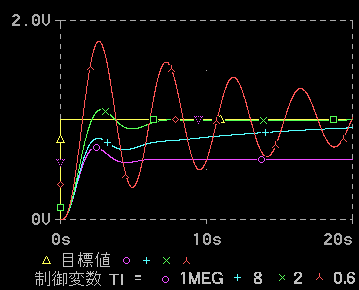
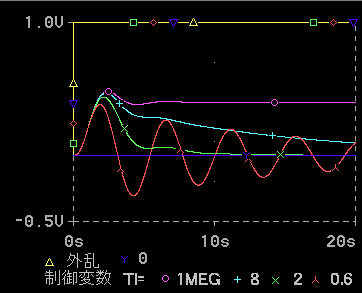
◆ 図は、比例ゲイン Kp の値を一定 (=1.5) にして、積分時間を変えたものです。積分時間 Ti を小さくすれば積分動作がよく効きます。Ti = 1MEG (≒∞)は積分動作なし (P 動作単独) を意味します。
比例ゲインを効かせ過ぎた場合(図 1-28、図 1-29)と同様に、積分を効かせすぎると、振動的になります。積分を適切に効かせれば、P 動作単独のときに比べて、若干応答が遅くなりますが、オフセットをなくす効果が、絶大です。
◆ I 動作 (積分動作)は、単独でも制御能力があります。したがって、I 動作のみの制御が可能です。しかし、図 1-33 に示すように、PI 動作と比べて、大幅に、制御応答が悪くなります。
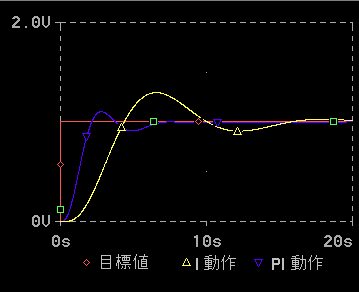
◆ アナログ制御の、初期の時代には、簡単で安くできる場合があることから、I 動作単独の制御が、使用されたことがあります。しかし、最近では、使用されることは、ほとんどありません。
◆ D 動作(微分動作)は、制御応答の改善に、使用されます。I 動作とは異なり、D 動作は、単独では制御能力がありません。P 動作と併用し、PD 動作 として使用します。PD 動作の演算式は、次のようになります(Kp : 比例ゲイン、Td : 微分時間)。
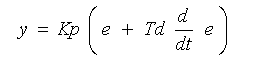・・・・ (1-4)
[注] 実際に使われているPD 動作の式は、これとは少し形が異なります。この演算式には、実用上の欠点があるからです。以下のシミュレーションでは、(1-4)式ではなく、実際に使われている式を、使用しています。
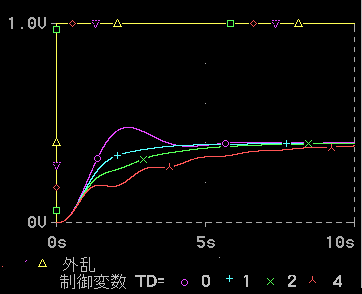
◆ 実験結果を、図 1-34 と図 1-35 に示します。この制御対象も「標準K」 です。比例ゲイン Kp を一定 ( = 1.5)にして、微分時間 Td を変えています。Td = 0 は微分なしです。
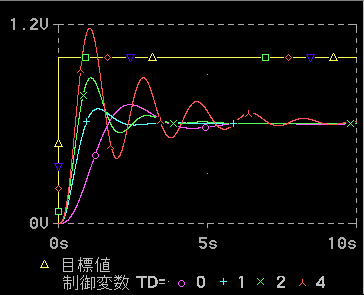
◆ 目標値変化の場合、P 動作単独 (微分時間 Td = 0) に比べて、制御応答が速くなっていることが分ります。D 動作も、効かせすぎれば、振動的になります。
外乱入力の場合は、P 動作では、オフセットがなくならないので、効果が若干分かりにくいのですが、制御応答が速くなったことによって、外乱の影響が減っていることが、分かります。
◆ オフセットも無くしたい、制御応答も速くしたい。この両方を満足させるには、PID 動作 を使用します(制御演算式は式 1-2)。シミュレーション結果を図 1-36、図 1-37 に示します。
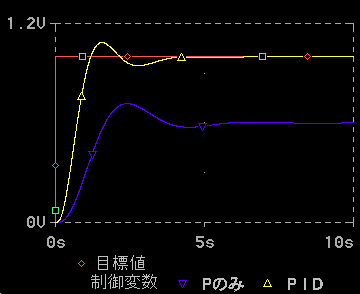
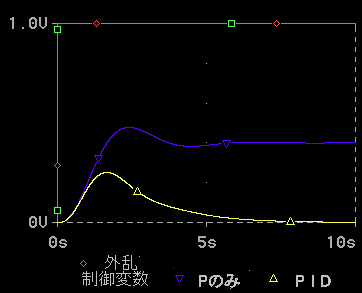
◆ I 動作と、D 動作の、両方の効果が現われて、良好な制御を行っているのが分かります。
[注] このシミュレーションも、実際に使われている式を使用しています。
一般のコントローラ製品(とくにディジタル製品)はPID 動作が普通です。これをPI 動作で使用しても、P 動作単体で使用しても、コストに違いはありません。
それならば、すべての制御に、最も良い制御成績が得られる筈の、PID 制御を使用すればよいように思われます。
しかし、世の中のあらゆるものには、長所と欠点とがあります。長所だけで、欠点無しというものは、存在しません。
いつでも、PID 制御が優れているとは、言えないのです。目的や用途によっては、PID 動作よりも P 動作、PI 動作、PD 動作のほうが適している場合も、あります。使い分けが、必要です。
◆ これまで見てきたように、制御応答は、制御対象の特性、制御演算式、およびその制御パラメータに依存して、大きく変わります。
制御対象と制御演算式とが決まれば、それに対して最も優れた応答を示す、最適な制御パラメータ の値 (PID制御であれば比例ゲイン Kp、積分時間 Ti、微分時間 Td )が、存在します。制御対象と、制御演算式に応じた、最適な、制御ぱラメータの値を求め、その値に設定することが、望ましい訳です。
では、どのような応答が、最適なのでしょうか。実は、最適な応答 も一定ではありません。
それぞれの制御対象によって、最適な応答波形が違います。最適な応答を、評価するパラメータが、複数存在し、それぞれの制御対象によって、どのパラメータを、重要視しなければならないのか、が異なるのです。
◆ 制御応答には、振動的な応答と、非振動的な応答とがあります。振動的応答における、制御成績を評価するパラメータ を図 1-38 に示します。
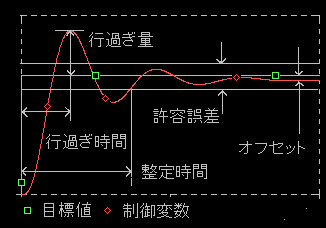
◆ 「許容誤差」はその対象システムにおいて許容される、偏差の値です。図に示されているように、この許容誤差は、初期の行き過ぎ状態が、収まった後の値です。許容誤差の値は、各制御対象によって異なります。
「行き過ぎ時間」は、応答における、最初のピークの位置までの時間です。
「整定時間」は最後に許容誤差の範囲内に入ったときの (すなわち、これ以降は許容誤差範囲内にあるという)時間です。
「行き過ぎ時間」と「整定時間」は、制御系の、即応性に関するパラメータです。非振動的な応答の場合には、「行き過ぎ時間」は存在しませんから、「整定時間」だけで、評価します。当然、これらの時間は、短いほど、好ましいわけです。
「行き過ぎ量」は、「行き過ぎ時間」における偏差量です。「オフセット」はすでに定義した通りです。この二つは偏差の大きさに関するパラメータです。
◆ 図 1-27 以降の各種制御応答を、比較すれば分かりますが、図 1_38 に示したパラメータは、互いに関連し合っています。しかも、あちらを立てれば、こちらが立たない、という関係があります。制御対象によって、何を重要視するかも、違ってきます。
最適な応答は、これらの妥協になります。したがって、高い汎用性を持った、総合評価指数は、存在しません。それぞれの制御対象ごとに、評価関数 を設定する必要があります。
◆ しかし、そうは言っても、何か、汎用的な目安がある方が便利です。世間で広く使用されている、評価関数があります。この評価関数も、万能では、ありませんが、かなり広い用途で、一応の目安になります。それは、次に示す、評価関数です。
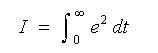・・・・ (1-5)
この評価関数の値は小さいほど優れています。評価関数の値が、偏差の 2 乗についての、面積になっていることから、2 乗誤差面積 と呼ばれています。
この形の評価関数は、制御だけでなく、広く使われている、評価関数です。数学的な取り扱いが簡単で、しかも比較的汎用性が高いからです。
ただし、制御成績の評価に使用する場合は、この評価関数は、あくまでも、1つの目安と考えてください。
◆ この評価関数は 2 乗してあることがミソです。単なる偏差だと、持続振動しているときに、プラスとマイナスが、互いにキャンセルされて、良い評価になってしまいます。2 乗によって、これを防げます。
また、2 乗することによって、評価が重み付けされます。偏差が大きいほど悪い評価になります。この意味でも、優れています。
この 2 乗誤差面積は、無限時間まで積分します。したがって、オフセットが存在するときは、2 乗誤差面積の値が、無限大となるため、利用できません。
制御成績が問題になるような、制御対象では、通常、I 動作(積分動作)を使用します。I 動作によって、オフセットが無くなりますから、この評価関数は一般性を失いません。
◆ (1-5)式を、評価関数とした、最適な制御応答の例を、図 1-39 の「行過ぎ有」に示します。図から分るようにかなり振動的です。
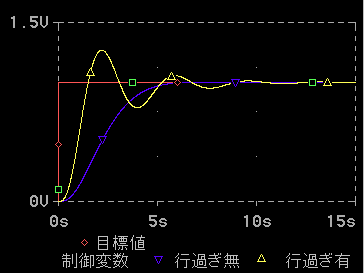
◆ 減衰振動では減衰率が定義されます。減衰率は隣り合うピークの振幅比です。この例では減衰率は約 5 です。
一般に、最適な応答の減衰率は 4 または、その近辺にあることが多いので、減衰率 4 の応答を、1/4 応答と呼んでいます。
評価関数が 2 乗誤差面積である、最適な応答の減衰率は、制御対象の特性や、制御演算式に依存し、一定の値ではありません。しかし、通常は、4 に近い値をとります。したがって 1/4 応答は、最適応答の、一応の目安になります。
ただし、ほぼ 1/4 応答であっても、最適応答から、かなり外れている場合もありますから、過信しないでください。
◆ 以上のように、2 乗誤差面積による、最適条件は、振動的な解になります。振動的であっても差し支えない制御対象では、多くの場合、一応は合理的な解です。
しかし、行き過ぎを許容できない制御対象も、たくさんあります。このときには、行き過ぎがないという条件の下での、2乗誤差面積を最小にする解を使用します。
このときの制御応答例が、図 1-39 の「行過ぎ無」です。
以上の二つが、最適応答の代表的な例です。両者を比較すると、評価関数の値は、行き過ぎ無しの方が、約1.9倍大きくなっています。
しかし、行き過ぎ無しの方が、速く落ち着いていることが分かります。許容誤差の値によって、どちらが優れているかが、異なってきます。
目的用途によっては、この中間の応答が、優れている場合もあるでしょう。制御対象によっては、もっと別な波形が、良いこともあり得ます。
◆ 制御演算式が P 動作の場合は、制御パラメータが比例ゲイン KP 1 つだけですから、最適応答をトライアルで求めても、それほど大変ではありません。
しかし、PID 制御では制御パラメータは 3 つあります。トライアルで、最適解を求める場合、トライアルする、パラメータの数が、問題になります。トライアルする、パラメータの数が多いと、必要なトライアルの数は、飛躍的に増大します。単なるトライアルではなく、効率良く、最適条件を求める手法が、必要です。
◆ これを「最適調整」または「パラメータ・チューニング」と呼んでいます。
