◆ 以下に、代表的な制御要素の、伝達関数と、その応答を示します。
◆ 1 次フィルタのことを、制御の分野では、1 次遅れ と呼んでいます。
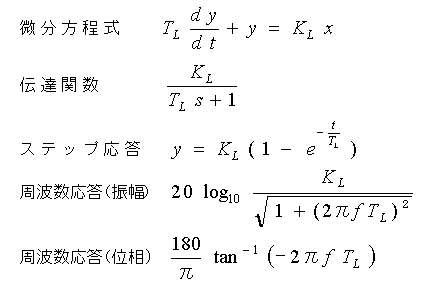・・・ (3-1-9)
式 3-1-9で、TL は時定数です。KL は定数でゲインと呼んでいます。f は周波数です。
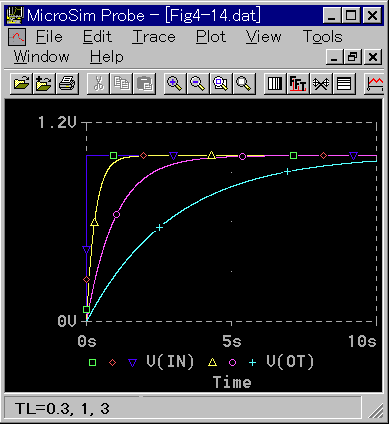
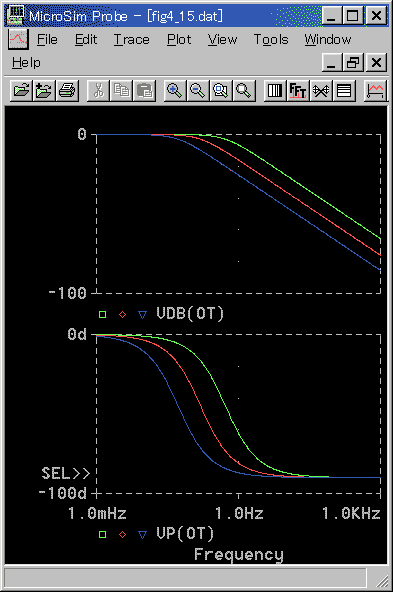
1 次遅れのステップ応答を図 3-1-16 に、周波数応答を図 3-1-17 に示します。
[注]
以降 PROBE画面は、原則として編集しないで、そのまま示します。
ただし、画面に複数曲線を表示しているときは、画面の下部に、パラメータ値などを示してあります。これは、元画面には無い、書き加えたものです。
◆ 1 次遅れにおいては、波形は全て同じ形をしています。そして、時定数 TL が小さいほど、即応性が高くなっています。
周波数応答においては、低周波の領域でゲインは水平、位相は 0°です。また、高周波の領域でゲインは -20 dB/dec (dec : 10倍) の傾斜、位相は -90°です。
[注 1]
ここのゲインは、周波数応答における振幅比です。ゲインの名は、色々なところに使われています。
[注 2] 周波数応答では、本当は、位相では無く位相差です。しかし、位相そのものが、元々、相対的な性質を持っていることから、位相差のことを単に位相と呼ぶことが多いのです。この講座でも、しばしば位相の言葉を使用します。
そして、低周波と高周波との中間の周波数では、なめらかに移行します。この、低周波と高周波の境を、カットオフ周波数 といいます。カットオフ周波数 fcは、
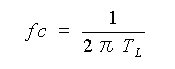・・・・ (3-1-10)
です。カットオフ周波数におけるゲインは -3 dB、位相は -45°です。
[ケース・スタディ 3-1-1]
★ 周波数応答の PROBE画面表示については、2.1.6.(2-B-c) 〜 (2-C-c)
を参照してください。
★ ステップ応答 (fg3_1_16.cir)、周波数応答 (fg3_1_17.CIR) のそれぞれについて、次の (a) および(b) のケース・スタディを行ってください。
(a) .PARAM KL=1 の KL の値を変えてみます。同じ入力に対して出力レベルが変化します。
(b) .STEP PARAM TL LIST の部分で、TL の値を変えてみます。応答速度が変化します。なお、複数の値を列挙するときは、降順または昇順のどちらかでなければなりません。
どちらの場合も、周波数応答では波形の形は変化せず、元の波形が平行移動します。この波形は 1次遅れに固有の波形です。
[注] ステップ応答も、見た目には形が変わりますが、本来の波形という意味では変わりません。
◆ すでに示したように、RCフィルタは 1次遅れです (2.1.6.(2-C))。
◆ 図 3-1-18 に示すタンクの液面 は、代表的な 1次遅れ系です。
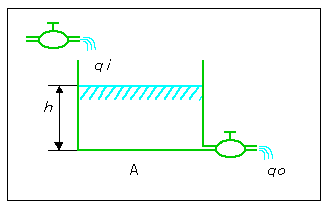
◆ タンクの断面積を A、タンク液面の高さを h、流入流量を qi、流出流量を qo とすれば、単位時間に qi - qo の液量がタンク内に蓄積され、液面 h を変化させます。したがって
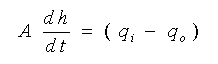・・・・ (3-1-11)
となります。流出流量は、液面が高くなるほど増加します。流出流量 qo が、液面高さ h に比例するとすれば、
h = R×qo
です。ただし、R は電気の抵抗に相当する比例係数です。また、液面 h は電気の電圧、流量 qo は電気の電流に相当します。したがって、
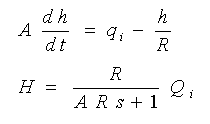・・・・ (3-1-12)
が成立します。
[注] 実際には、流出量は液面高さには比例はしません。しかし、近似的に比例すると、考えることができます。
◆ 2次遅れ とは、伝達関数の分母が s の 2次式であるものです。1次遅れ要素を 2個カスケード接続すると、2次遅れになります。
この形の 2次遅れは、すでに 2次フィルタとして紹介しました (2.1.6.(2-F))。
2次遅れは、さらに一般化して、伝達関数を
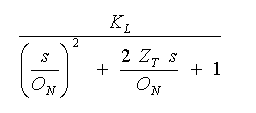・・・・ (3-1-13)
の形で表わすことができます。ここで、ON を固有角周波数 、ZT を減衰係数 といいます。
角周波数とは角速度 のことです。角速度 ω と周波数 f は比例関係 (ω = 2πf) にあります。したがって、どちらを使用しても、単位が異なるだけで、同じことを表わします。一般に、実用上は周波数を、理論上は角速度を使用します。
◆ 周波数応答のグラフの横軸は、周波数応答の名前からは、周波数のはずです。しかし、周波数応答と称するグラフで、横軸を角速度で目盛ることが、しばしばあります。このようなことから、角周波数という言葉が生まれました。
固有角周波数という用語は、本来の「固有周波数 」という用語から派生したものです。
[注 1]
一般に角速度は ω で、減衰係数は ζ で表わします。しかし、SPICE では英文字しか使えません。しかも大文字と小文字とが区別されません。
[注 2]この講座では、SPICE で使用する式は、SPICE で使用する記号と統一するために英大文字で表記します。また、式 (3-1-13) では、添え字を使用していますが、SPICE では、添え字は存在しませんから、通常文字になります。
◆ 2 次遅れには 3 つのパラメータがあります。このうち、ゲイン KL は 1 次遅れのゲイン KL に、固有角周波数 0N は 1 次遅れの時定数 T に対応します。
1 次遅れと同様に、ゲイン KL はゲインを変え、固有角周波数 0N は応答速度を変化させます。波形を変えることはありません。これに対して、減衰係数 ZT は波形を大きく変えます。
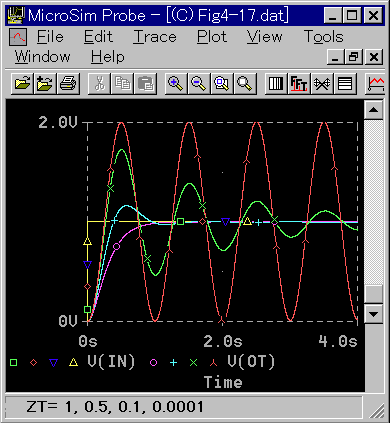
◆ ステップ応答を図 3-1-19 に、周波数応答を図 3-1-20 に示します。
[図 3-1-19] 2次遅れ (ZT < 1) のステップ応答
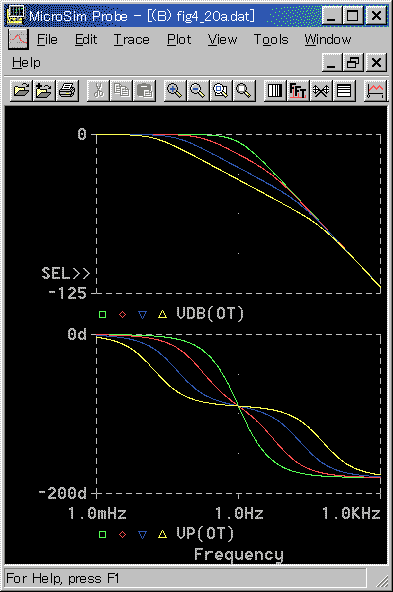
[図 3-1-20] 2次遅れ (ZT < 1) の周波数応答
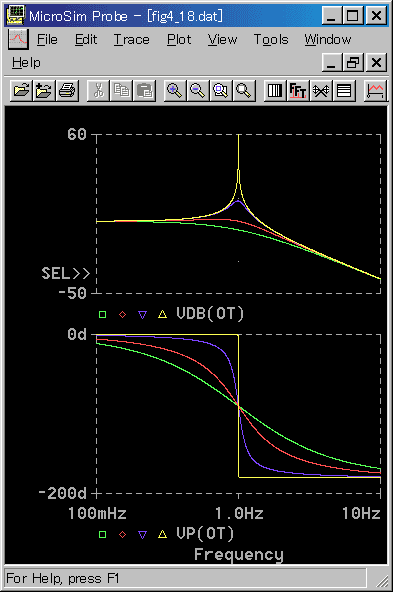
◆ この条件では、振動的な解になります。とくに、ZT = 0 では持続振動になります。 0 < ZT < 1
では減衰振動で、ZT が大きいほど減衰が大きくなります。
減衰係数 ZT = 0、すなわち制動がない自由振動(持続振動)のとき、振動の周波数は固有周波数 fN (= ON / 2π) になります。ZT > 0 のとき、振動の周波数は低くなりますが、僅かです。
解が振動的であるということは、共振 が発生していることを意味します。このことが、周波数応答に現われています。すなわち、ゲインが 1 よりも高くなり、ピークを作っています。
完全な共振状態では、持続振動になります (ZT = 0)。このときゲインは無限大です。
この ZT < 1 の条件は、伝達関数の分母をゼロと置いた方程式
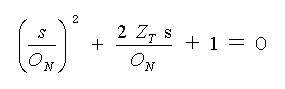・・・・ (3-1-14)
の根が、複素数となるときです。この、伝達関数の分母をゼロと置いた方程式のことを、特性方程式 といいます。
◆ この条件では、非振動的な解となります (図 3-1-21 〜図 3-1-22)。
[図 3-1-21] 2次遅れ (ZT < 1) のステップ応答
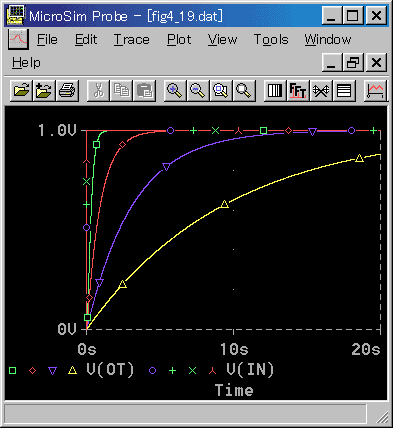
[図 3-1-22] 2次遅れ (ZT < 1) の周波数応答
◆ 特性方程式の根は実根です。根が実数であるということは、因数分解できるということです。すなわち、図 3-1-23 の形で表わすことができます。
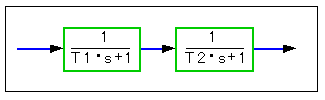
◆ 減衰係数 ZT = 1 のときに、特性方程式の根が等しく (重根) なります。すなわち、T1 = T2 です。
ZT が大きくなると、T1 と T2 との差が大きくなります。この条件では、2 つの 1 次遅れが分離した形になります。周波数応答では、低周波の部分は、1 次遅れの特性を示します。そして、周波数が高いところで、2 次遅れの特性が現われます(3.2.2.コラム 3-2-2 参照)。図 3-1-22 の ZT = 30 (黄)は、この特徴が良く現われています。
◆ 全体として、2 次遅れでは、低周波領域で、ゲインは水平、位相は 0°です。また、高周波領域では、ゲインは -40 dB/dec、位相は -180°になります。
そして、カットオフ周波数 fc は、fc = 1 / 2πON です。カットオフ周波数においては、位相は -90°です。ゲインは、減衰係数が ZT < 1 のときはピークを作ります。これらの特性は、2 次遅れに固有の性質です。
このように、周波数応答では、制御要素の伝達関数の形と波形の特徴が、良く対応しています。
このことから、逆に、制御要素の周波数応答の波形を調べることによって、その制御要素が伝達関数の形で、どのように近似できるかを推定することができます。
★ fg3_1_19.cir 〜 fg3_1_20 について行います。何れも減衰係数 ZT の値を変えてみてください。
fg3_1_19.cir では、減衰係数と振動減衰の関係に注目してください。
fg3_1_20.cir では、減衰係数の値が小さいとき、ゲインのピークがシャープなだけでなく、位相の変化が急峻になっていることに注目してください。
★ fg3_1_19.cir では、減衰係数の値が大きいと遅れが大幅に大きくなっています。減衰係数の値が大きいと、図 3-1-23 に示した 1 次遅れの時定数 T1 と T2 の差が開き、大きい方の時定数の値も大きくなります。
このため、1 次遅れとしての 2 つのカットオフ周波数の差が開き、中間の周波数領域で、大きい方の時定数を持つ 1 次遅れに近い特性が現われます。
★ また、ゲイン KL、固有角周波数 ON も変えてみてください。
★ なお、シミュレーション自体に興味がある読者は、次のことも試みてください。
fg3_1_19.cir 〜 fg3_1_20.cir では、減衰係数の値をゼロにしないで、十分小さい値にしてあります。この値を真にゼロにするとどうなるでしょうか。
また、fg3_1_20 では、AC 解析の点数 (2.1.6.(1-B) 参照) を 1000 と大きく取ってあります。この点数を (大幅に) 変えると、波形 (とくにシャープなピーク、ZT = 0 のときを含む) にどのような影響があるか、試してください。
◆ 減衰係数が大きくて、2 つの 1 次遅れと見なすことができる場合については、2.1.6.(2-E) 〜 (2-F) の RC 2 段回路に示しました。
次に、インダクタ L とコンデンサ C とからなる、LC 回路 を考えてみます。LC 回路と称していても、一般には、インダクタに存在する抵抗分 R を無視することはできません。また、積極的に抵抗を加えることもあります。図 3-1-24に示すように、RLC回路を考える必要があります。
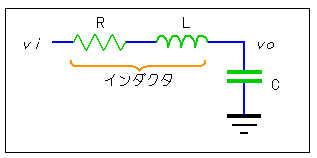
◆ インダクタ L は、インダクタに加わる電圧 v と電流 i の関係が、コンデンサとはちょうど逆になっています。すなわち、
v = L di/dt
です。したがって、インピーダンスは jωL で伝達関数は Ls です。
図 3-1-24 から分かるように、VO の点は (抵抗 + インダクタ) とコンデンサとの分圧となります。したがって、
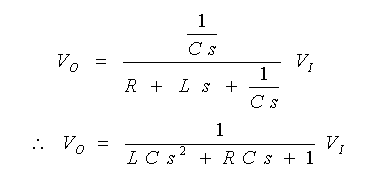・・・ (3-1-15)
となります。ここで、抵抗 R が小さいと、減衰係数が 1 よりも小さくなり、振動的な解になります。
