


◆ モータのフィードバック制御は、速度制御と位置制御の 2 つに大別されます。まず速度制御について解説します(図 6-2-1)。
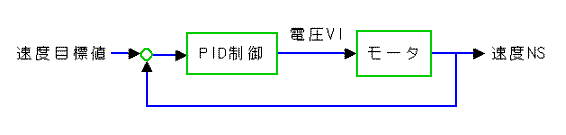
◆ なお、この講座では、特定のモータをモデルとしてシミュレーションを行います。この講座で述べていることは、大略の傾向は同じですが、定量的には、個々のモータや負荷によって、異なります。
◆ シミュレーションには、アナログ制御を使用します。ディジタル制御も、サンプリング周期が十分短ければ、アナログ制御で近似されます(1.5.(5)、4.2.3.(3-B))。
また、ここの目的は、モータの制御応答を調べることです。ディジタル制御の特性を調べる必要はありません。
コントローラは、サブサーキット PIDAW を使用します。このサブサーキットは、制御出力にリミッタがあり、リセットワインドアップ防止を含んでいます(5.5.(3))。
モータの制御では、リセットワインドアップを考える必要はありませんが、コントローラ出力にリミットがある場合の応答が必要になります。
[注] PIDAW は、デフォルトでは、リミットが無く、普通の PID 制御のサブサーキット PIDA と同じに動作します。アナログ PID 制御は、全て、PIDAW を使用して差し支えありません。
◆ ここまでの説明では、コントローラは、全て、シミュレーションの上で取り扱ってきました。実際に制御を行うときは、製品としてのコントローラです。この両者は、比例ゲイン KP の定義 が異なります(図 6-2-2)。
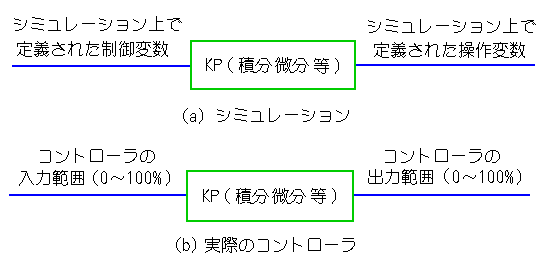
◆ したがって、シミュレーションで得られた、比例ゲイン KP の値を、そのまま実際のコントローラに使用することはできません。換算する必要があります。
なお、積分時間や微分時間は、そのまま使用することができます(秒と分など単位の換算は必要です)。
◆ アナログ制御、ディジタル制御どちらの場合にも、モータ制御では、スイッチング制御が使われます。
アナログ制御であっても、スイッチング制御は非連続な制御です。ディジタル制御は、もともと非連続ですが、通常のディジタル制御とは異なります。
アナログ、ディジタルを問わず、スイッチング制御について、検討する必要があります。ただし、スイッチング制御は、次章の解説となります。
◆ モータ速度制御の制御応答を、図 6-2-3に示します。
[図 6-2-3] モータ単体 速度制御(出力リミット無し)
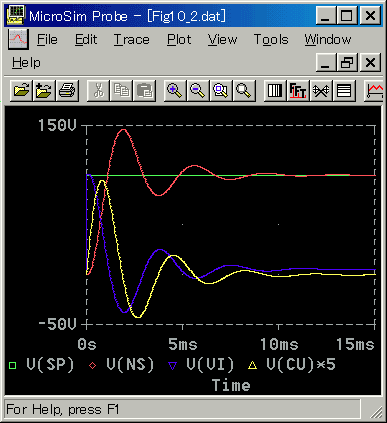
◆ ほぼ最適な応答になるように、制御パラメータを調整してあります(3.3.2 コラム 3-3-1)。PI 動作で、比例ゲイン KP = 1、積分時間 TI = 10ms です。
[注]
PI 動作の代わりに、PID 動作を使用すれば、制御応答を、さらに改善することができます。
しかし、その改善の程度は大体推定できます(3.2.4.(4-E))。この講座では、PI 動作で検討します。
良好な制御を行なっています。減衰がありませんから、電流 CU の定常値はゼロです。ただし、無視できるとはいっても、実際には、僅かな減衰がありますから、微少な電流が必要です。
電圧 VI の定常値は約 5.3V です。これは、モータの回転によって発生する逆起電力に対抗する電圧です。
起動時には、電圧/電流はピークを作り、VI ≒ 100V、CU ≒ 18A です。起動時には、起動トルクを必要としますから、それをまかなうためのピークです。
★ 図 6-2-3 では、制御変数のほかに、各種の変数を表示しています。
制御応答を解析し、制御応答を改善するためには、制御変数だけでなく、関連する各種変数の挙動を知ることが有効です。
また、制御対象の特性自体を、良く理解することができます。
実際の制御対象では、ふんだんにセンサを付けて、計測するわけには行きません。また、測定不能な変数もあります。
★ ただし、実際の制御においても、必ず存在し、かつ非常に役に立つ変数があります。
それは、コントローラの出力です。制御変数を記録するとき、同時にコントローラ出力を記録すると有効です。
解析や、トラブルシューティングに、活用してください。
★ シミュレーションでは、コントローラ出力はありませんが、操作変数を利用できます。本当は、実際でも、操作変数の値の方が、さらに有用なのです。
やむを得ず、コントローラ出力で代用するのですが、それでも非常に役立ちます。
◆ モデルは線形ですから変数の変化範囲に制約はありません。±無限大に変化可能です。
しかし実際の制御系には、必ずリミッタ特性があります(5.5.(2-A))。
リミッタに引っ掛かれば、変化範囲が制限されますから、それによって制御応答に遅れが発生します。より良い制御を望むなら、実際の使用条件において、リミッタに引っ掛からないように、制御系を設計しておくことが必要です。
しかし、これを実現するために、たとえば、電源電圧を高くしたり、大電流を出力できるように、しなければなりませんから、装置のコストアップにつながります。
差し支えない程度に、ピーク時の応答を抑える方が良い場合が多いと考えられます。予め、シミュレーションによって、リミッタが働いたときの応答を検討しておくことが、有効です。
◆ モータにおいては、操作変数の変化範囲のリミットを考える必要があります。電源装置の出力電圧範囲です。
この例では、電圧の定常値は、5.3Vです。電源装置の出力電圧範囲を 100V にすることは大き過ぎます。
電源装置の出力電圧範囲を、±24V にリミットしたときの、制御応答を図 6-2-4 に示します。比較のため、リミッタ無しも入れてあります。
[図 6-2-4] モータ単体 速度制御(出力リミット有り)
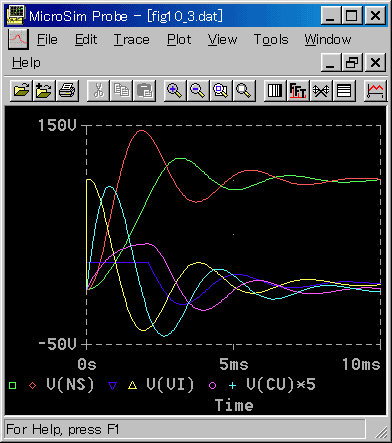
◆ 出力電圧 VI がリミットされ、その結果として電流 CU のピークも、8.3A に減少しています。その代わり、制御応答が、ぐんと、遅くなっています。
一般に、リミットに引っ掛かるような、大きなステップ状の目標値変化は、モータのスタートアップ時に発生します。
スタートアップ時の立ち上がりが、遅くても良ければ、電源電圧を低く押さえることができます。
電圧の低い電源装置を使用すれば、電流値も低く押さえられますから、電源装置のコストを引き下げることができます。
一般にスタートアップ以外は、目標値の大きなステップ状の変化はありません。また、スタートアップをステップではなく、あるシーケンスで徐々に加速する場合も多いでしょう。
スタートアップ時以外の通常の操作では、リミッタに引っ掛からないようにすれば、応答が遅くなることは、ありません。
◆ 以上のほかに、電流値には、実用上の制約があります。電流値が大きいと、発熱量が増えます。
またさらに、永久磁石形モータでは、過大な電流によって発生する磁界が、永久磁石を減磁 させてしまうという、現象があります。
永久磁石が減磁すると、モータの性能が低下してしまいます。この減磁が起こらないように、電流をリミットする必要があります。
このモータで、電源電圧を100V以上に取り、リミッタ無しの運転をすれば、実は、この減磁の問題に引っ掛かります。電源電圧を押さえることによって、過大電流を防止することは、このためにも必要なことです。
◆ モータには、上記のように、電流値の制約があります。電源電圧が低くても、異常時には過大電流が流れる可能性があります。通常、電流制限回路 を設けて、過大電流を防止します。
ただし、電流制限回路は、異常対策です。スタートアップも含めて、正常動作時に、電流制限回路が動作しないように、システムを設計する必要があります。
モータには、定格電圧と定格負荷があります。定格電圧以下の電源電圧で、定格負荷以下の負荷で使用するように設計します。
電流制限回路は、異常対策ですから、シミュレーションモデルに、電流のリミットを組み込む必要はありません。
★ 図 6-2-3 の制御は、本物で実験すれば、モータを損傷します。シミュレーションなら、実行することができます。
★ 耐圧が10Vの部品に1kVの電圧を掛けても、100Wのモータに、1MWの電力を加えても、パソコンから火を吹くことはありません。
そしてその条件で、もし部品が正常に働いたとしたら、どうなるかを、ちゃんと示してくれます。
★ 安心して、極端な条件を、試してみることができる。これも、シミュレーションの効用の一つです。
◆ トルク TD の外乱に対する応答を、図 6-2-5 に示します。比較のため、リミッタ無しも入れてあります。
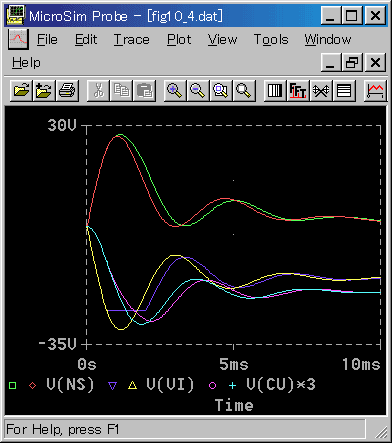
◆ 外乱のステップ幅は制御変数 回転速度 NS の振れ幅が、目標値変化と大略等しくなるように選びました。
この条件では、僅かですが、電圧VIにリミットが掛かっています。通常は、このように大きなステップ状の外乱はありません。
外乱は、十分に打ち消すことが必要です。一般論としては、予想される外乱に対して、操作変数がリミットに掛からないように、制御系を設計します。ただし、このケースでは、リミッタへの引っ掛かりが僅かですから、リミッタの影響は、余りありません。
目標値変化のときと、制御パラメータの値は、同じに取ってあります。目標値変化に比べて積分動作の応答が緩やかになっています。これは、制御一般の傾向と同じです(3.2.4.(4-E))。
外乱としてトルクが掛かりましたから、それを駆動するために、電流 CU の定常値が発生し、それによって外乱のトルクを打ち消しています。
◆ 次に追値制御の例を示します。簡単な例として、台形制御を行ないます(図 6-2-6)。
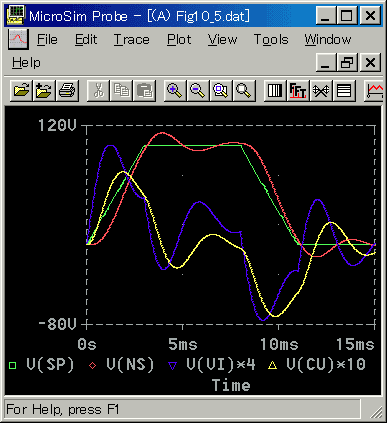
◆ DC モータですから、ステッピングモータのような問題(6.1.3.(1))は、ありませんが、スタートアップ、シャットダウンを緩やかにする目的で、使用されます。
この例では、目標値 SP の変化速度が速いので、十分に追従していません。
しかし、ステップ応答のときと異なり、操作変数 VI の値はリミットに達していません。ステップ応答と比べれば、変化速度が緩やかなので、偏差の値が大きくならないからです。
外乱も、通常は変化速度が緩やかなので、外乱の大きさが大きくても、偏差は小さな値です。
目標値の変化速度が十分に低いときは、図 6-2-7 に示すように、目標値に対して良く追随します。
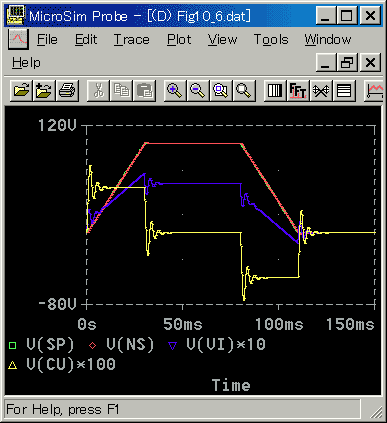
◆ 当然、追値制御は、通常このような使い方をします。図 6-2-6 は、応答を理解するために、故意に普通でない使い方を示したものです。
回転速度 NS が、一定速度で変化しているということは、加速度が一定だということです。これはトルク一定を意味し、さらに電流値 CU が一定であることを意味しています。このとき、電圧 VI は、一定速度で変化しています。
また、回転速度が一定のときは、トルクがゼロで、電流 CU もゼロです(減衰係数 ゼロ を仮定)。
さらに、最初の立ち上がりの部分を拡大して眺めて見ましょう(図 6-2-8)。
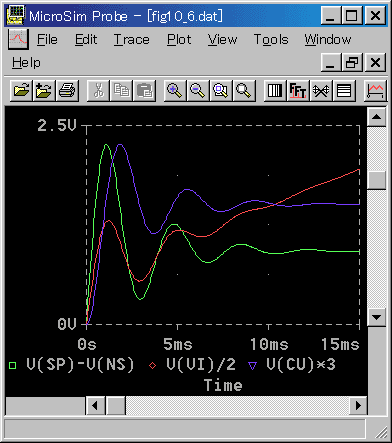
◆ 拡大波形を見やすくするために、少し細工をしてあります。回転速度 NS の代わりに、偏差 SP - NS を示してあります。
図 6-2-7 を見ると、回転速度の立ち上がりは、目標値と一致しているように見えます。しかし一致しているのではなく、一定の遅れを持っています(1.3.(1-B))。したがって、偏差は、一定値に落ち着いています。
応答波形を見ると、減衰振動になっています。
この応答は、定常偏差がありますから、最適調整に、直接、2乗誤差面積を使用することができません。したがって、1/4 応答を、最適調整の目安に使用します。
次に、立ち上がりから水平に移る部分の拡大波形を、図 6-2-9 に示します。
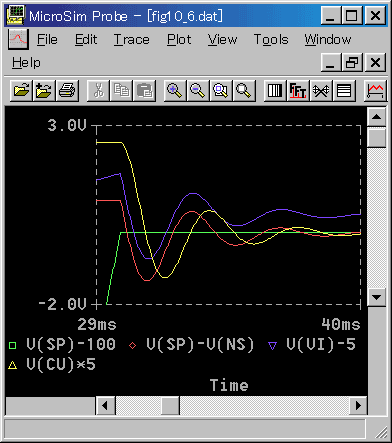
◆ これも、波形の表示を、細工してあります。図の変数の説明を見れば、意味は分かると思います。この部分の応答は、目標値が一定になるのですから、積分動作が効いて、偏差はゼロになります。
波形そのものは、立ち上がりのときと、ほぼ同様です。