


◆ 基本式の周波数応答を図 4-2-7 に示します。なお PI 動作 は、実用式を使用しても、基本式と同じです。違いはありません。
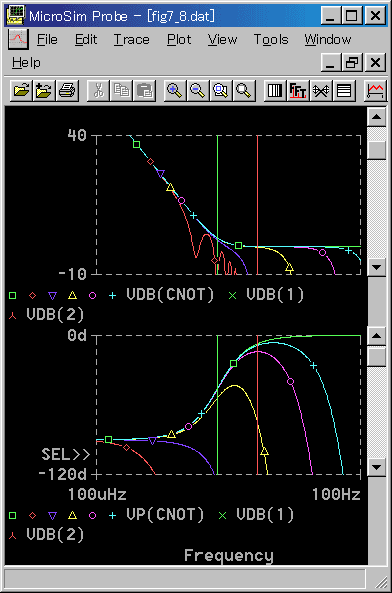
◆ サンプリング周期 TS を変えたときの特性の変化を示してあります(積分時間 TI 固定で、TI / TS を変化)。また、比較のために、アナログ制御の特性も付加してあります。
積分時間 TI は、標準Kの制御対象
で良い制御制御成績が得られる、限界感度法から、さらに修正した値に合わせてあります(3.3.3.(4-B)表 3-3-3)。
十分低い周波数では、アナログの特性と良く一致していますが、周波数が高いところでは、とくに、TI / TS の値が小さいときは、大幅に異なっています。
周波数応答を評価するときは、安定限界における周波数付近の周波数帯域に注目する必要があります(3.2.2.(5))。限界周期 TU と積分時間 TI を周波数に換算(コラム 4-2-3 参照) すると、表 4-2-1 になります。
| - | 時間 | 周波数 |
|---|---|---|
| 限界周期 TS | 2.23 | 0.45 |
| 積分時間 TI | 2.77 | 0.057 |
◆ この周波数の位置を図に表示してあります。
アナログと大きく異なるのは、高周波における位相の遅れです。アナログとほぼ同等なのは、TI/TS=500、せいぜいTI/TS=100です。
また、TI/TS≦1では、位相の立ち上がりがありません。これは、たかだか I 単独動作としてしか働かないであろうことを意味しています(3.2.4.(2-C))。
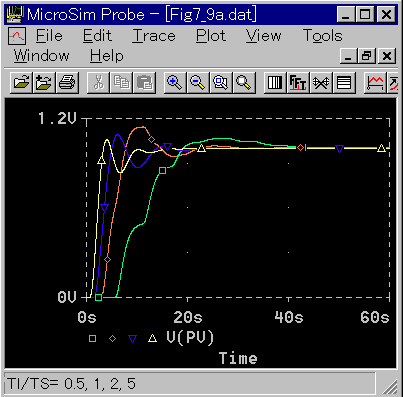
◆ サンプリング周期を変えて制御を行なった結果を図 4-2-8、図 4-2-9 に示します。
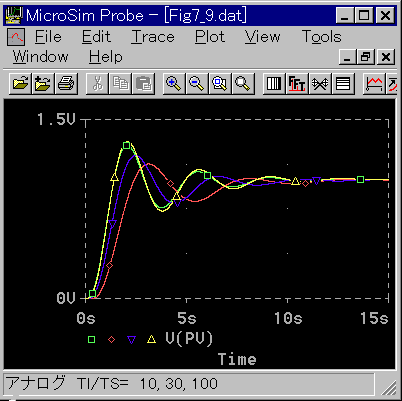
[図4-2-9] PI 動作(基本式)の制御応答(その 2)
◆ サンプリング周期 TI / TS = 100 は、アナログと良く一致しています。
サンプリング周期 TI / TS ≦ 30 では、制御パラメータの値をアナログ制御よりもゆるくする必要があります。TI は、そのままで、KP を小さくしました。
制御成績は、TI / TS が小さくなるにつれて、次第に悪くなります。
とくに TI / TS = 0.5 は波形が妙な形になっています。これは、サンプリング周期が、制御対象の特性に比べて長いために、サンプリング毎に、ステップ応答になっていると考えられます。遅れは大きいですが、ちゃんと制御しています。
この現象を確認するために、制御対象を 1次遅れにした、シミュレーション実験を行いました(図 4-2-10)。
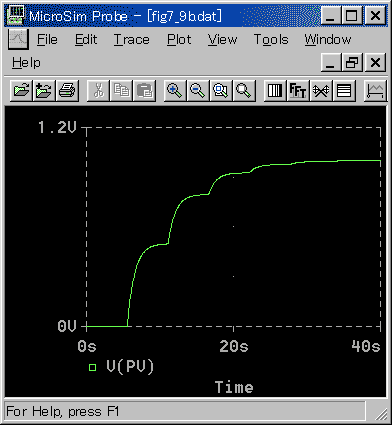
◆ サンプリング周期毎に、1次遅れのステップ応答が連続しています。この実験から、上記の推定は、確かなものと思われます。
シミュレーションは、このように、理由や予想を確かめるために、簡単な実験を行うことができます。実験の結果は、確実な証拠とすることはできませんが、良い状況証拠になります。
表 4-2-2 は、制御成績を評価関数の値(アナログ制御に対する相対値)で示したものです。図 4-2-11 は、サンプリング周期と評価関数との関係です。
[表 4-2-2] サンプリング周期と制御成績の比較(PI 動作)
| サンプリング周期( TI / TS ) | 0.5 | 1 | 2 | 5 | 10 | 30 | 100 |
| 比例ゲイン( KP ) | 0.25 | 0.5 | 0.7 | 1.0 | 1.4 | 2.0 | 2.8 |
| 評価関数の値( Id / Ia ) | 10.4 | 5.4 | 3.4 | 2.2 | 1.6 | 1.2 | 1.06 |
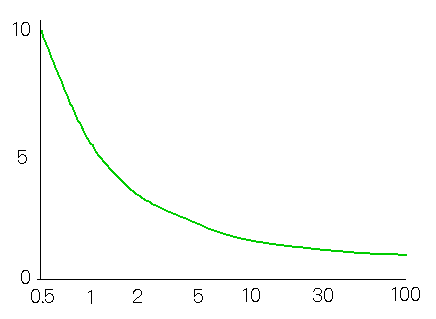
◆ TI / TS の変化の割には(とくに TI / TS が大きい範囲では)、制御成績の違いは、案外少ないことが分かります。
すなわち、制御成績が、アナログよりも、若干悪くなることを許容すれば、サンプリング周期を大幅に延ばすことが可能です。
★ 1 次遅れ要素には、カットオフ周波数があります。1 次遅れ要素の時定数を TL、カットオフ周波数を fc とすれば、式 3-1-10 が成立します。
カットオフ周波数 は、1 次遅れ要素の周波数応答において、位相が -45°、ゲインが -3dB になる周波数で、ゲインが水平から -6dB / dec の傾斜に移る周波数を示しています。
★ 周波数応答におけるこの性質は、1 次遅れ要素だけでなく、PI 動作や、PD 動作においても見られます。
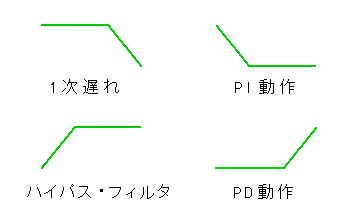
★ 図は、周波数応答を、折れ線近似で表わしています。折れ点の周波数がカットオフ周波数です。
PI 動作や PD 動作では、積分時間 TI、微分時間 TDが、1 次遅れの時定数 TL と同じ意味を持っています。
★ 複数の制御要素をカスケード接続したとき、全体の特性は、ボード線図上では加算になります(コラム 3-2-2)。そして、各々のカットオフ周波数のところに折れ点ができます。
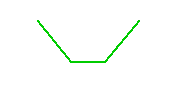
図は、PI 動作と PD 動作とを組みあわせた PID 動作です。
★ PID 制御の最適調整を行うと、積分時間 TI と微分時間 TD とが接近しているため、実際の特性曲線では、水平の部分がなく、極小値を持った曲線になります。
このようなときは、PI 動作と PD 動作とに、それぞれカットオフ周波数を考えるよりも、一つの極小値の周波数を考える方が合理的でしょう。この周波数は、ほぼ二つのカットオフ周波数の幾何平均となります。
★ なお、最適調整における限界周期 Tu は、正弦波形の周期です。時定数ではありません。限界周期と限界周波数との関係は、
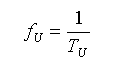
です。時定数とカットオフ周波数との関係(式 3-1-10)とは異なります。
◆ PD 動作 は、I 動作を含みませんから、時間領域形と周波数領域形との違いは、ありません。基本式と実用式の差は、フィルタの有無です。
◆ 基本式の周波数応答を図 4-2-12 に示します。
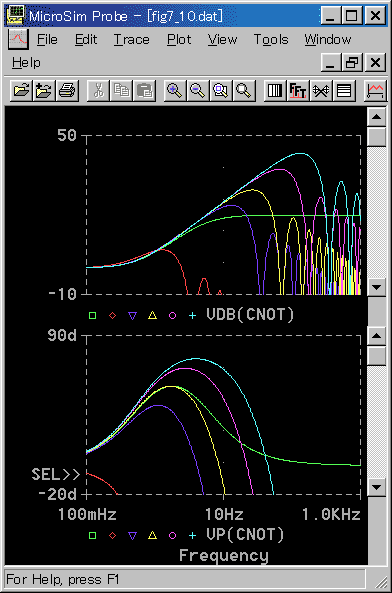
◆ サンプリング周期が短いと、位相の進みはアナログよりも大きくなり、効能は高くなります。しかしゲインのピークが高く、副作用が大きくなります。そして、TD / TS = 20 で位相、すなわち微分効果がアナログとほぼ一致しています。
この TD / TS = 20 のとき、ゲインについては、ピークの値がアナログよりも約 9dB 高くなっています。しかしさらに高い周波数では、アナログよりも小さくなります。
副作用に関しては、制御対象のノイズ状況により異なり、一概には言えません。まあ、アナログと同等と考えて良いでしょう。ノイズの問題については、5.4.(3)を参照してください。
TD / TS ≦ 1 では、位相の進みがありません。したがって、微分効果は期待できないと考えられます。
◆ PD 動作(基本式)においては、サンプリング周期を適切に選ぶなら、アナログと同等の制御が期待できます(図 4-2-13)。
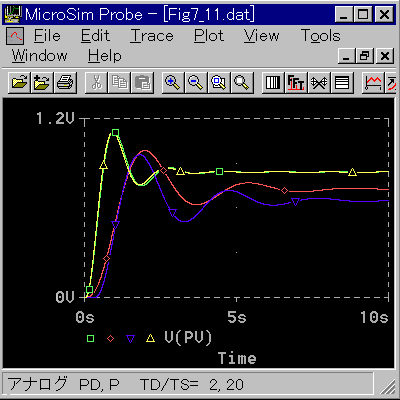
◆ 予想通り、TD / TS = 20 で、アナログの PD 動作(緑)とよく一致しています。
サンプリング周期を長く(TD / TS = 2)すれば、応答は遅くなります。しかし、アナログのP動作(赤)と、ほぼ同等の制御成績になっています。アナログの P 動作と同等の制御成績で良い場合には、サンプリング周期を長くできるという、効果があります。
◆ 実用式の周波数応答は、図 4-2-14です。
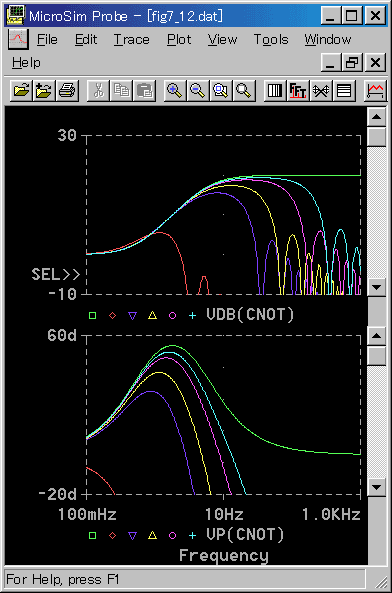
◆ 実用式にはフィルタが入って入ますから、サンプリング周期が十分短いと、アナログの特性と一致します。しかしサンプリング周期が長いと、サンプリングの影響が表われます。
アナログと同等と見なすことができるサンプリング周期は、フィルタが入っている分、基本式よりも小さくなります。アナログと十分に一致したと見なせるのは、TD / TS = 50 以上です。
しかし、TD/TS=10 でも、かなりの効果は期待できそうです。
実用式(実はフィルタの効果)は、サンプリング周期が十分に短い範囲では、サンプリング周期を微分時間に連動させることなく、固定できる点が便利です。
基本式(実はフィルタ無しの特性)では、サンプリング周期が短すぎると、特性が悪くなります。
ただし、実用式は、基本式に比べて、同じ微分効果を得るためには、サンプリング周期を、基本式よりも短くしなければならない、という欠点があります。
◆ PID 動作 の基本式の周波数応答を図 4-2-15 に、実用式の周波数応答を図 4-2-16 に示します。縦の補助線は、PI 動作のものと同じ意味です。
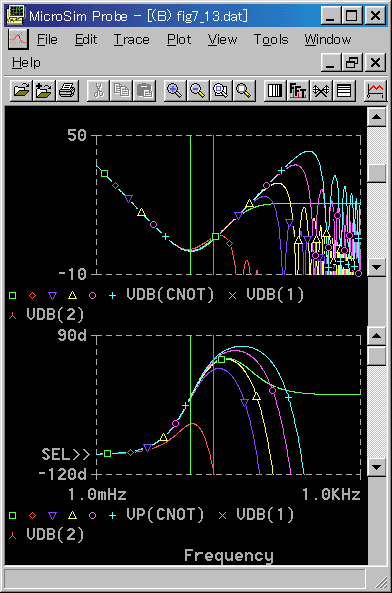
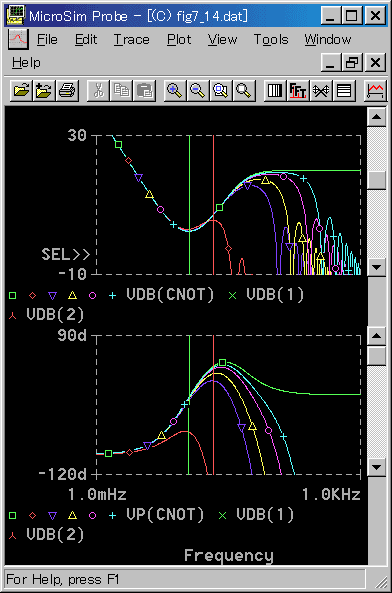
◆ 基本式は、時間領域のアナログと比較しています。
TI と TD の値は、いずれも、アナログ制御において、限界感度法を適用したときの最適条件(限界感度法の値を修正したもの 3.3.3.(4-B) の表 3-3-4 の値です。限界周波数は、0.45Hz です。
積分動作についてはアナログと良く一致しています。
微分動作に関しては、PD 動作と同様に評価できます。基本式では、TD / TS = 20 で、アナログと同等です。それよりも TD / TS が大きいときは、微分効果は高くなりますが、副作用も大きくなります。
実用式は、限界周波数付近においては、TD / TS = 20 で、アナログよりも劣ります。それより TD / TS が増加したとき、アナログに近付きます。
◆ さらに、TD / TS = 20 における、実用式と基本式とを、比較してみます(図 4-2-17)。
[図 4-2-17] 実用式と基本式の比較(TD/TS = 20)
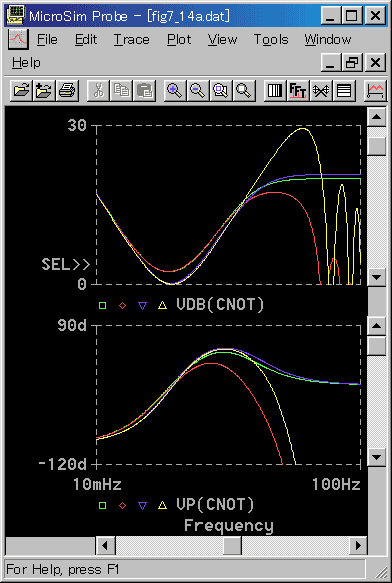
◆ 両方とも、アナログとの一致度が高いので、アナログの差が、ディジタルにも、良く現われています。
すなわち、ゲインにおいて、基本式よりも実用式の方が、谷底の高さが高くなっています。これは、周波数領域形と時間領域形との違いです。
なお、図 4-2-15 と図 4-2-16 から分かるように、この時間領域形と周波数領域形との谷の高さの違いは、TD / TS の値に関係なく成立します。
[ケーススタディ 4-2-2]
★ PID 動作で、積分時間 TI を、図 7-14、15 のケースよりも大きくして、図と同様な周波数応答を求めてください。
★ なお実用価値はありませんが、逆に TI の値を小さくしたらどうなるかを試みるのも面白いでしょう(なぜ実用価値が無いかが分かります)。
◆ 周波数応答の検討によって、十分推定されると思いますが、ステップ応答で確認して見ましょう。
基本式の制御応答を、図 4-2-18 に示します。
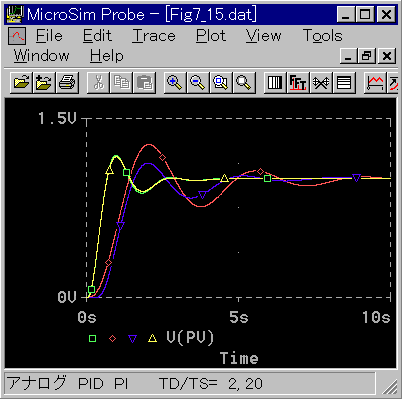
◆ 比較対象のアナログ制御は、時間領域形です。
PD 動作と同様に、TD / TS = 20 で、アナログと良く一致しています。
また、PD 動作と同様に、アナログの PI 動作と同等の制御成績で良いならば、D 動作を活用することによって、サンプリング周期を長く取ることができます(TD/TS = 2)。
◆ 実用式で、アナログに近い応答例を、図 4-2-19 に示します。
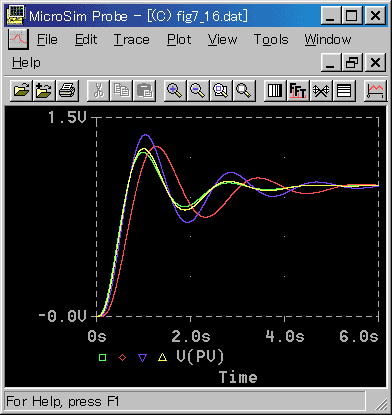
◆ TD / TS = 100 は、アナログと同等の応答です。TD / TS = 20 も、かなり良い応答です。
TD / TS = 10 になると、若干遅れが目立ちます。しかし、D 動作の効果は、十分に認められます。
次に、TD / TS が小さいところを、図 4-2-20 に示します。
[図 4-2-20] PID動作(実用式)の制御応答(TD/TS 小)
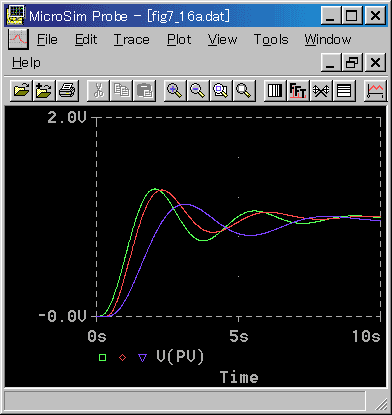
◆ TD / TS = 2 は、アナログの PI 動作と同等の制御を行っています。ほぼ同じサンプリング周期のディジタル PI 動作と比較すれば、かなり応答が速くなっています。4.2.2.(2) 図 4-2-6 のところで、「それなりの効果は期待できるかも知れません」と述べたことは、確かだっだのです。
以上、PID 動作の、制御成績をまとめると、表 4-2-3 になります。
[表 4-2-3] サンプリング周期と制御成績の比較(PID動作・実用式)
| サンプリング周期 TD/TS | 2 | 10 | 20 | 100 |
| 比例ゲイン KP | 1.5 | 3.1 | 4.4 | 4.4 |
| 積分時間 TI | 1.6 | 2.2 | 2.2 | 2.2 |
| 微分時間 TD | 0.50 | 0.72 | 0.72 | 0.72 |
| 評価関数 Id/Ia | 2.7 | 1.5 | 1.3 | 1.03 |
◆ 実用式は、制御対象の特性に対して、サンプリング周期を十分に短く取ることができる、コントローラを使用する場合には、サンプリング周期を十分短い値に固定しておくとくことができる、という利点があります。
しかし、制御対象の特性に対して、サンプリング周期を十分に短く取れないときは、同じサンプリング周期で制御応答が優れているという点では、基本式が勝っています。
◆ ここで、同時出力形と中間出力形について、ちょっと眺めて見ましょう。PID 制御(基本式)の同時出力形の周波数応答を図 4-2-21 に、次回出力形との比較を図 4-2-22 に示します。
[図 4-2-21] 同時出力形(PID 基本式)の周波数応答
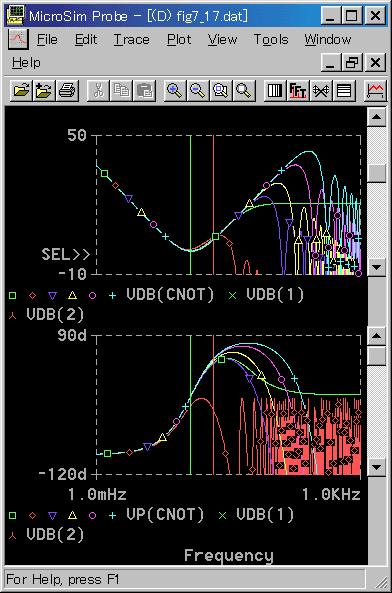
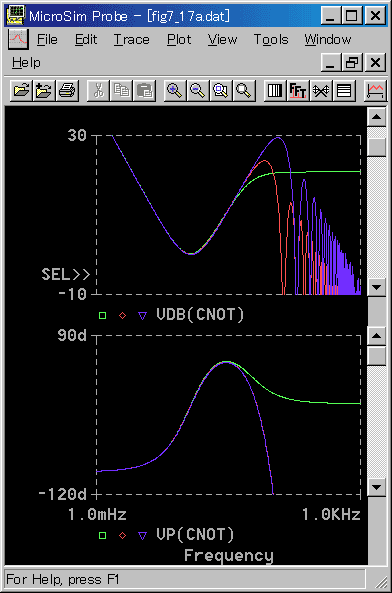
◆ 同時出力形の TD/TS = 10 と次回出力形の TD/TS = 20 の特性が、高周波部分を除いて、良く一致しています。これは、同じ制御応答を得るのに、同時出力形は、次回出力形に対して、サンプリング周期を 2 倍にできることを意味しています。
同時出力、中間出力(50% 時点)、次回出力の制御応答の差が、図 4-2-23 です。
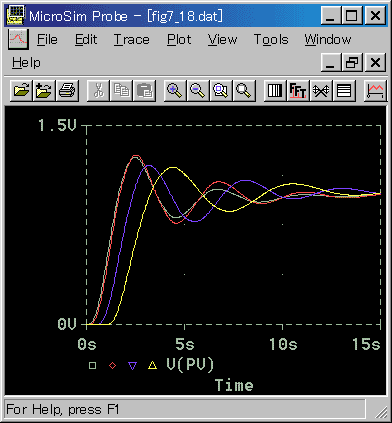
◆ サンプリング周期が長いほど差が大きいので、サンプリング周期が長いところ(TD / TS = 1)を取ってあります。
制御成績の面では、同時出力形の優位性は歴然です。しかし実用上、同時出力形を実現できるのは、限られた条件のときだけです。
ただし、中間出力形であっても、サンプリング周期に比べて出力までの時間が短いときは、制御成績は、かなり改善されます。
マイクロプロセッサを他の演算処理と共用しているときは、制御変数の入力から操作変数の出力までの間に、他の演算処理が入らないようにして、出力までの時間を最短にすることが非常に有効です。
ディジタル制御では、マイクロプロセッサの多重処理機能を活かして、1 台のマイクロプロセッサで、多数の制御ループを処理することがあります。
このような場合には、1 つの制御ループについて、制御演算と、出力処理との間を空けないで、続けることが有効です。
1 台のマイクロプロセッサで、10 ループを処理する場合(図の TL = 0.1)には、実用上、同時出力形と見なすことができます。