


◆ DC モータ単体の応答を、シミュレーションモデルで調べて見ます。シミュレーションの対象モータの仕様を、表 6-1-2 に示します。以降、この講座では、原則として、このモータを使用します。
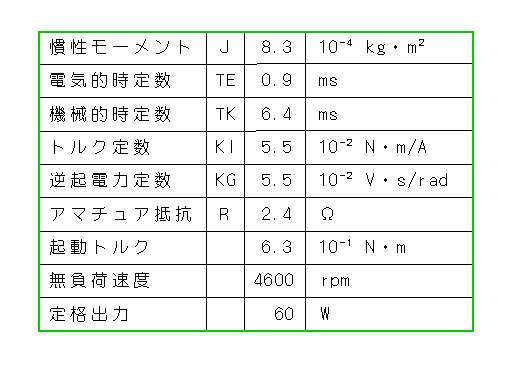
◆ 表のモータは、減衰を無視できますから、減衰係数は記載してありません(6.1.4.(2-A))。しかし、シミュレーションで検討するのですから、ループのままの方が汎用性があります。
サブサーキットのモデル(図 6-1-22)で、減衰係数 DN をゼロとします。これを、2 次遅れモデル と呼ぶことにします。2 次遅れモデルは、図 6-1-23 の上側です。
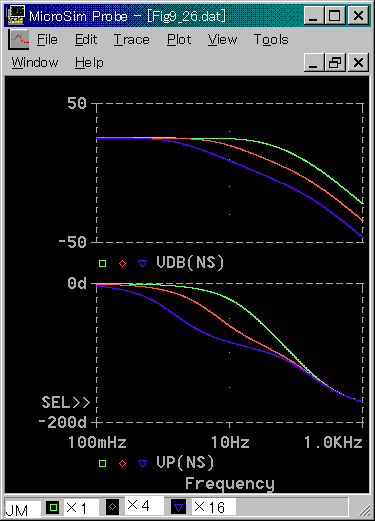
周波数応答を図 6-1-27 に示します。入力はモータに加える電圧です。
[図 6-1-27] モータ単体の 2 次遅れモデル(周波数応答)
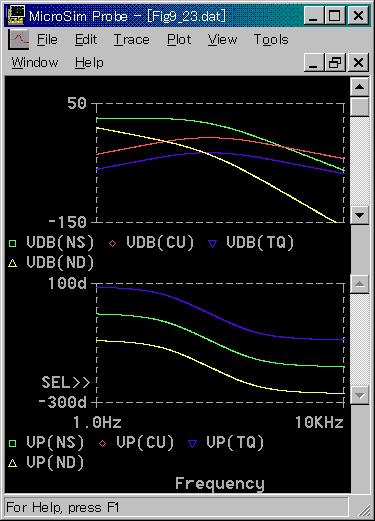
◆ 出力の回転速度 NSは、当然 2 次遅れになっています。
電流 CU と、トルク TQ は、低周波領域(定常状態)でゲインが低くなってゆき、位相はプラス 90°になっています。これは、微分の特性です(3.1.3.(5-B-b))。
2 次遅れモデルでは、トルク TQ (力 F)は、積分要素を経由して回転速度 NS (速度 V)になっています。したがって、積分要素を経由する前の波形は、経由した後の波形に対しては、微分された形になっているのです。
トルク TQ の特性は、微分 + 2 次遅れの特性です。したがって、高周波領域は 1 次遅れの高周波部分の特性を示します。そして中間に、ゲインのピークがあり、位相がゼロの点があります。
電流 CU も、トルク TQ と同じ波形です。
回転角度 ND は、低周波領域でゲインが高くなってゆきます。定常状態では、回転速度 NS は一定値です。それを積分していますから、定常値が無限大になります。位相も回転速度 NS より 90°遅れています。
◆ 仕様には、機械的時定数が示されています。この値を使用して、図 6-1-24 の「さらに近似したモデル」でシミュレートして見ます(図 6-1-28)。
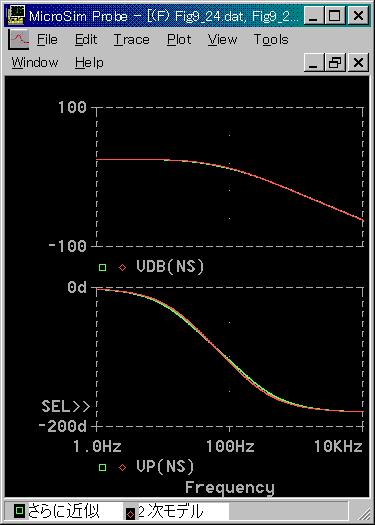
◆ 比較のために、図 6-1-27 の波形も表示してあります。非常に良く一致しています。この近似が成立する条件は、式(6-1-3) でした。
このモデルでは、TK (機械的時定数) / TE (電気的時定数) = 7.1 > 4 です。一応式(6-1-3) を満足している程度ですが、少なくともこの場合には、十分に良く一致しています。
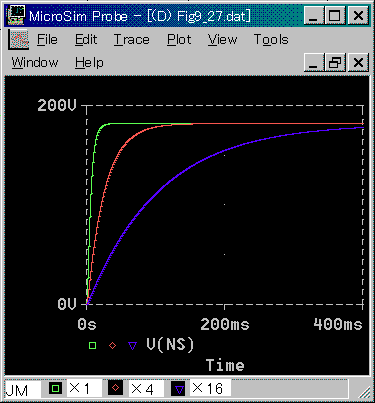
◆ モータ単体の 2 次遅れモデルの、ステップ応答を図 6-1-29 に示します。
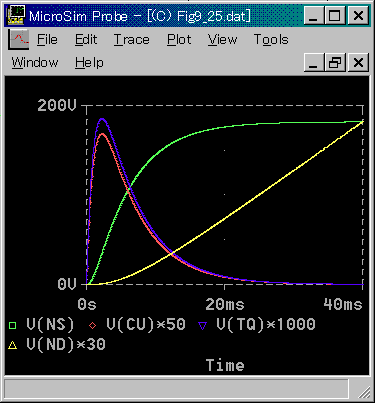
◆ 回転速度 NS は、2 次遅れですが、2 つの 1 次遅れの合成で近似されますから、非振動的な波形です(3.1.3.(2-B-b))。
電流 CU とトルク TQ は、遅れを含む微分特性の波形です。定常状態の値はゼロです。これは、系に減衰係数を含まないからです。
無視できる程度に小さいとはいっても、実際には、減衰係数はゼロではありません。その分若干の定常電流が流れ、定常トルクがあります。
定常状態では一定回転速度ですから、回転角度 ND は一定速度で増加します。
★ 図 6-1-28 の表示は、回転速度 NS を基準にしています。このため、他の変数は縦軸のスケールが大幅に異なります。図を見易くするように、縦軸をスケール変換しています(変換係数は図に表示されています)。
シミュレーション・モデルを作成するとき、各変数について、本来の単位をそのまま使用したからです。SPICEは、アナログ・シミュレーションですが、内部の演算はディジタルであり、浮動小数点演算を使用しています。
★ このため、各変数のスケールが大幅に異なっても、精度を損なわずにシミュレーションを行なうことができます。
この特徴を活かして、各変数をスケール変換しないでシミュレートしました。SPICEでは、各変数の値を、ディジタルで表示させることができますから、値を間違いなく読み取ることができます。
★ ディジタルコンピュータではなく、アナログ回路を使用した、真のアナログシミュレーションでは、シミュレーション上でのスケールがほぼ揃うように、スケール変換を行なって、シミュレーション・モデルを作成する必要があります。
これをやらないと、誤差が非常に大きくなり、使い物になりません。真のアナログシミュレーションは、ディジタル演算の固定小数点演算に相当します。
★ スケール変換したモデルを作るのには、手間が掛かります。また、単に相対的なアナログ波形を見るのには問題ありませんが、数値を読み取るとき、スケールを取り間違えるというミスを犯す可能性もあります。
この点、SPICEは楽です。
◆ この講座での負荷は、6.1.4.(3)に示した、慣性モーメントで代表される負荷に、限定します。負荷を掛けると、モータ単体と比べて、2 つの変化が現れます。1 つは、等価的に慣性モーメントが増加することによる、応答の遅れです。
もう 1 つは、モータ単体では無視できた、減衰係数が無視できなくなる場合が、出てくることがあります。
先ず、慣性モーメント増加の影響を調べて見ましょう(図 6-1-30、図 6-1-31)。
[図 6-1-30] 負荷(慣性モーメントJM 増加)の影響(周波数応答)
[図 6-1-31] 負荷(慣性モーメントJM増加)の影響(ステップ応答)
◆ 負荷の増加にしたがって、応答は遅くなります機械的時定数の値は、図 6-1-24に示されているように、慣性モーメント J (質量 M )の値に比例します。
電気的的時定数 TE は変化しないで機械的時定数 TK だけが増加します。
このモデルは、2つの 1 次遅れの合成で近似されます。機械的時定数の増加にしたがって、2つの 1 次遅れの時定数の差が大きくなり、分離された形になります(3.1.3.(2-B-b)、3.2.2.コラム3-2-2)。
◆ 負荷が、大きな摩擦を持っていれば、減衰係数が大きくなります。負荷が、ほとんど摩擦だけの場合を想定して、慣性モーメントの大きさが、モータと同じであるときの、減衰係数の増加の影響を調べます。
図 6-1-32、図 6-1-33に、回転速度の応答を示します。
[図 6-1-32] 回転速度における負荷(減衰係数増加)の影響(周波数応答)
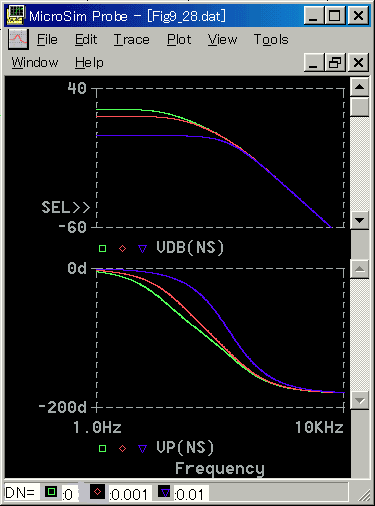
[図 6-1-33] 回転速度における負荷(減衰係数増加)の影響(ステップ応答)
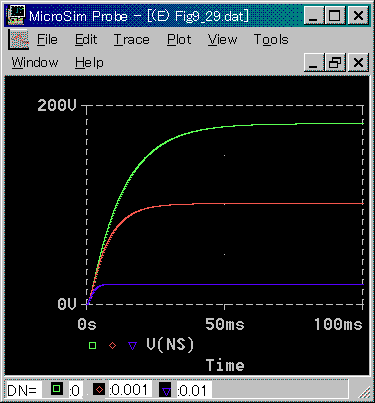
◆ 減衰があれば、定常状態における回転速度は低くなります。しかし、減衰係数が大きい方が、応答は速くなっています。応答は速くなりますが、振動的になるのではなく、逆の方向です。
応答が速くなるのは、メカ時定数が小さくなるからです。メカ時定数 TM の値は、図 6-1-20に示すように、減衰係数 Kv に反比例します。
次に電流値を見て見ましょう(図 6-1-34、図 6-1-35)。
[図 6-1-34] 電流におけ負荷(減衰係数増加)の影響(周波数応答)
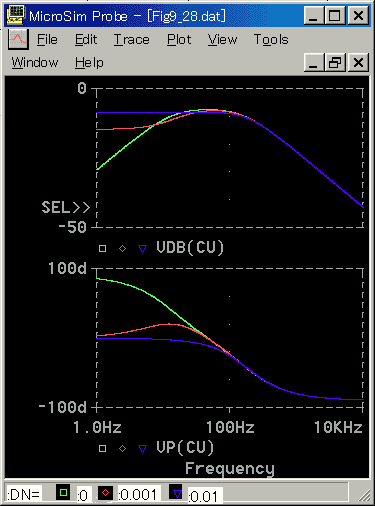
[図 6-1-35] 電流におけ負荷(減衰係数増加)の影響(ステップ応答)
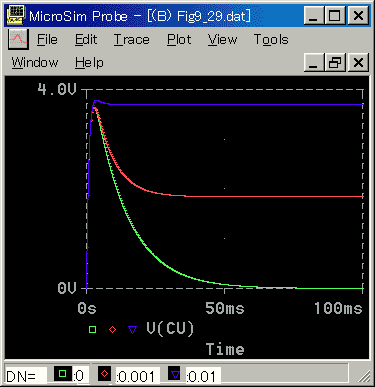
◆ 減衰がありますから、定常状態において、減衰に対抗して回転するためのトルク、したがって電流が必要です。すなわち、電流も定常電流が流れます。
減衰が大きくなるにつれて、微分特性が減っていきます。減衰が大きいと微分特性が消えて、1 次遅れ特性となります。減衰係数が 0.01 のとき、ちょうど微分が無くなっています。