


◆ 線形 とは、入力と出力との関係が直線で表されることです。非線形 は、入出力間が線形ではないことです。
基礎的な制御理論は、システムの線形性を前提としています。非線形だと、理論的取り扱いが非常に難しくなるからです。しかも非線形の問題は、ケースバイケースであり、汎用的な取扱ができません。
しかし実際には、システムの各所にさまざまな種類の非線形が存在します。
幸いなことに、多くの場合は、非線形を線形近似 して、線形系として取り扱うことができます。そして、それなりの成果がえらます。
入出力間の静特性が曲線で表わされる形の非線形では、非線形の程度が高くても、変数の変化範囲が、小さいときは、線形近似することができます(図 5-20)。
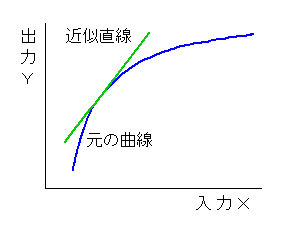
◆ 良好に制御されているときは、変数の変化範囲は小さいですから、この近似が有効です。
しかし、簡単な非線形であっても非線形系として取り扱わないと実際と大きな差が出る場合もあります。
以下この種の非線形で重要なものについて説明します。
これらの非線形は、理論的に取り扱うと、一般にかなり、面倒です。しかし、シミュレーションを利用すると、比較的簡単に解析することができます。
◆ 非線形の問題は、AC 解析では取り扱えません。
AC解析は、小信号入力として解析されます(2.1.6.(1-C))。静特性が曲線で表わされる、図 5-13 の非線形の場合には、線形近似されたものの AC 解析が得られます。
その他の非線形の場合には、全く異なった解が出てきます(たとえば、4.1.4.(3-C-a))。
非線形を、非線形として解析するためには、トランジェント解析を使用する必要があります。
◆ 最も多く現われる、というよりも現実には必ず存在すと言ってよい非線形性は、変数の変化範囲に限定があることです。すなわち、入力がある範囲を超えて変化しても、出力は変化できずに一定となります(図 5-21)。
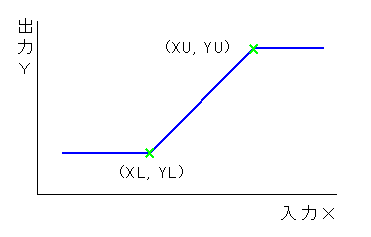
◆ このような非線形特性をリミッタ特性 (飽和特性 )と呼んでいます。
線形とは、入力と出力の関係が直線で表わされることです。そして直線は、-∞から+∞まで変化できるとことを意味します。しかし実際の変数には、必ず変化範囲があり、それを超えることはできません。
線形は、理想化された、非現実のものです。この意味では、リミッタ特性は、あるのが当然です。
ただし、実際上、リミット値を越えることが無いような使い方をしていれば、リミッタが存在することを、無視することができます。多くの場合に、線形理論を適用することができるのは、この理由によります。
◆ 制御系におけるリミッタは、少なくとも 図 5-22 に示すところに存在します(図の∨)。
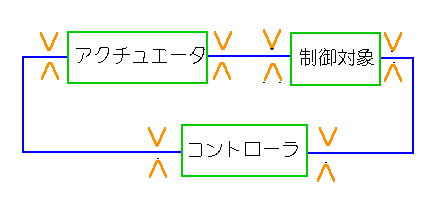
◆ 各制御要素の入出力のところに存在します。このうち、例えばコントローラ出力の 0〜100% が、アクチュエータ入力の 0〜100% に対応するといったように、マッチングが取られていれば、どちらか一方を考えればよいわけです。
マッチングが取れていなければ、厳しい方を考えればよいので、結局半数になります。
なお、制御対象が複雑な場合には、制御対象内部の思わぬところが、リミッタになっている場合がありますから、注意する必要があります。
★ アクチュエータ は、制御対象に働きかけて、制御変数を変化させます。制御出力の範囲は、アクチュエータの能力で評価することが必要です。
アクチュエータの能力が十分でないと、制御変数の値を十分に変化させることができません。
★ アクチュエータの能力は、目標値の変化範囲に対応できることは当然として、さらに予想される外乱の範囲に対して、十分に対応できる能力を持っていることが必要です。
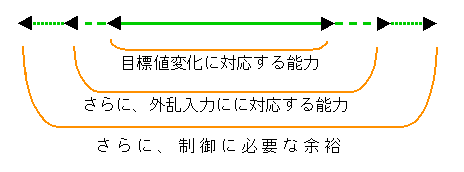
★ このとき、さらに考えに入れておかなければならないのは、制御を行うための余裕です。この余裕がないと、十分な応答性が得られません。
一方、アクチュエータに余裕を持たせるということは、一般により大きな、したがって、高価なものを必要とします。
この意味では、余裕を持ち過ぎることは、損です。
★ また、もう一つ考える必要があることは、アクチュエータの最小出力です。
ゼロから、ある値まで出力するアクチュエータ(たとえば水量を絞るバルブ)を考えます。
最小出力(水量)をゼロにできる場合であっても、通常は、ゼロまで連続的に滑らかに出力することはできません。
★ ゼロの付近では、オンオフ的に変化することが多いのです。
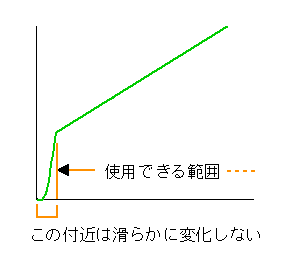
★ したがって、連続的に滑らかに制御できる範囲は、最大値だけでなく、最小値を考えなければなりません。
実際に使用できる最大値と最小値との比を、アクチュエータのレンジアビリティ といいます。
アクチュエータを選択する場合には、このレンジアビリティを考える必要があります。この意味でも、大は小を兼ねません。
◆ リミッタは、PSPICEでは、簡単に作ることができます。
アナログ・ビへービア・モデルの別の形式、テーブルによる非線形の表現を使用してリミッタを作ることができます。
書式は、
E<名称><+ノード><-ノード>TABLE {<式>}=<<入力値>,<出力値>>*
( < > は、必須 [ ] は、省略可能 *は、繰り返し可能)
で、入力値を結ぶ折れ線が、出力値を結ぶ折れ線に変換されます。テーブルの最小値と最大値は、それぞれ外側に延長されます。
したがって、テーブルで2点を指定すれば、それがそのままリミッタです。記号を図 5-21のように取れば、
<<入力値>,<出力値>>* → (XL,YL) (XU,YU)
とします。
◆ なお、この講座では使用していませんが、周波数応答を、テーブルの形で表すことができます。実測などによって得られた周波数応答を、伝達関数の形で近似することなく、直接周波数テーブルの形で利用することができます。
書式は、
E<名称><+ノード><-ノード>FREQ {<式>}=<<周波数値>,<振幅値>,<位相値>>*
( < > は、必須 [ ] は、省略可能 *は、繰り返し可能)
です。
◆ ただし上記のテーブル方式は、データの値をパラメータ(2.2.3.(1-C)、2.2.4.(1-E))にすることができないなど、使い勝手がよくありません。
そこで、使いやすいサブサーキットLIMITを用意しました。これは、図 5-23 の回路をモデル化したものです。
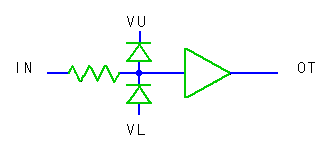
◆ ダイオードで電圧をリミットする回路です。実際にアナログのリミッタ回路として使用されている回路です。
ダイオードは、順方向に電圧を加えると電流が流れ、逆方向だと電流を阻止します。
ただし順方向に電流が流れるとき、順方向電圧が発生します。
しかもこの順方向電圧は、完全に一定ではありません(図 5-24)。
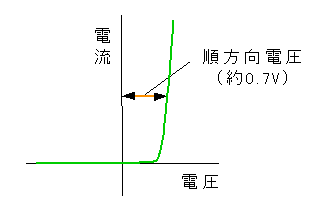
◆ PSPICE で用意されているダイオードのモデルは、実際のダイオードの特性を模擬ししていますから、この順方向電圧があります。
しかし、このサブサーキットでは、順方向電圧がほぼゼロである架空のダイオード・モデル(2.1.5.(2-G))、DIDEAL を作り、このダイオードを使用しています。
したがって、リミッタはほぼ理想的に動作します。
このダイオード・モデル DIDEAL は他にも色々と便利に利用できます。ライブラリ CONT.LIB に入れてありますから、自由に使ってください。
◆ サブサーキットLIMIT は、
* 出力 入力 高リミット 低リミット .SUBCKT LIMIT OT IN PARAMS: VH=1MEG VL=-1MEG
です。
電圧値は、VH>VL であればよく、共にプラスまたは共にマイナスで差し支えありません。
デフォルトは、1MEG V/-1MEG V ですから、実用上リミットなしになります。
1 方向だけにリミットを掛ける場合は、リミットを掛ける方だけをパラメータ指定します。
◆ コントローラの出力は、出力範囲による、リミッタ特性があります。一般的には、制御出力が制限されることは、等価的に遅れとして働いて、制御成績を悪くします。
PD 動作における制御応答を図 5-25 に、そのときのコントローラ出力を図 5-26 に示します。
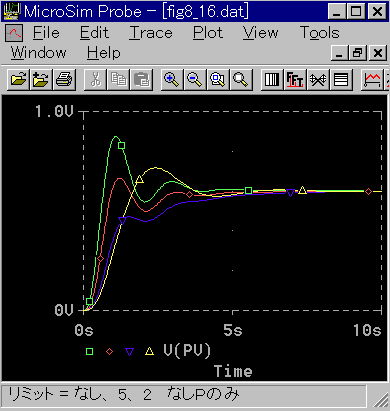
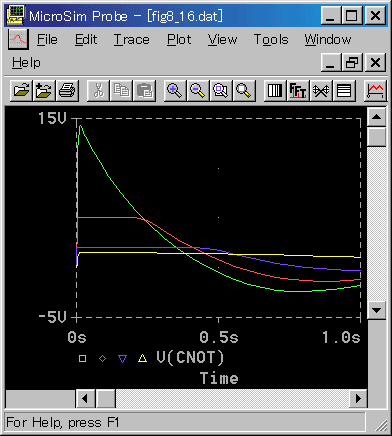
◆ 3.2.4.(3-B)図3-2-43と同じ条件で、リミッタの影響を調べたものです。
黄は比較のための、リミット無しのP動作のみです。
PD 動作で、かつステップ応答であるため、コントローラ出力の立ち上がりが大きく、そのためリミッタの影響が強く現われています。リミッタが強いほど、立ち上がりの遅れが大きくなっています。
リミット = 5 では、立ち上がりの遅れが行き過ぎを減少させ、それが適度に働いて、応答を改善しています。
リミット = 2 では、リミットされたことによって、微分効果が無くなっています。
図では、リミット値を変えていますが、実際には、故意にリミッタを入れるのではなく、コントローラ出力の 0% と 100% がリミッタとして働く場合が多いと考えられます。
そして、コントローラ出力が 0 または 100% に達したということの原因が、アクチュエータの能力不足に帰着されることになるでしょう。
◆ 微分動作を効かせたのに、制御成績が改善されない、といった原因が、案外こんなところにあったりします。
◆ リミッタによる悪影響が最も顕著に表れるのが、リセットワインドアップ の現象です。
積分動作は、偏差があるとそれを積分します。したがって偏差をゼロにする能力を持っています。
しかしこの積分効果が、制御にとってマイナスに働く場合があります。これがリセットワインドアップの現象です。
リセットワインドアップは、制御対象の特性によって、あまり影響が無いときと、顕著に現われる場合とがあります。
◆ リセットワインドアップの現象が現われやすい制御対象を、PI 動作で制御したときの制御応答を図 5-27 に示します。
制御対象は、サブサーキットPRCS(3次遅れモデル)を使用していますが、リセットワインドアップが、よく現われるように特性を変えてあります。
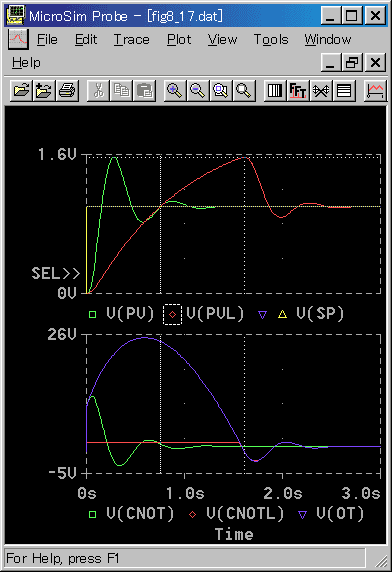
◆ リセットワインドアップは、コントローラを、手動から自動に入れて、最初に動作し始めるときに発生する現象です。
図の上段は制御変数で、下段はコントローラ出力です。リミッタ付は、リミッタなしに比べて、著しく遅れが大きくなっています。これがリセットワインドアップの現象です。
積分動作は、偏差がある限り変化しつづけます。とくにスタートアップの初期は偏差が大きいので、コントローラ内部の制御出力 OT (青)は、急速に増加します。しかしリミッタがあるので、外部への出力は CNOTL (赤)で頭打ちになります。
しかし、CNOT が頭打ち、すなわち 100% ということは、制御変数 PVL を増加させる値です。したがって、制御変数 PVL は、増加し続けます。
コントローラの演算が頭打ちとなり,減少に転じるのは、PVL がほぼ目標値を過る時点です(図のカーソル1)。この時点でもなお、PVL は増加を続けます。そして、実際に PVL が減少に転じるのは、CNOTL が、減少し始めた以降です(カーソル2)。
これがリセッワインドアップの現象です。積分動作があるために、著しい行きすぎと遅れが発生します。
◆ 制御対象が標準Kの場合にも、リセットワンドアップは発生します(図 5-28)。
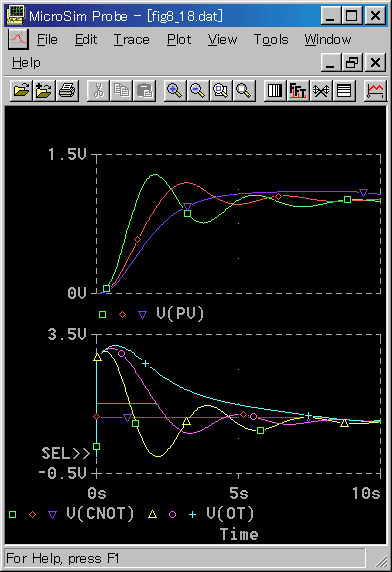
◆ リミット = 1.5 では、リミッタのために制御応答は遅くなっていますが、リセットワインドアップは発生していません。
リミット = 1.1 でリセットワインドアップが発生しています。しかし、偏差は大きくありません。リセットワインドアップの現象はわずかです。
リセットワインドアップは、制御対象によって、顕著な場合と、あまり問題ない場合とがあります。
◆ リセットワインドアップの原因は、出力がリミットされているにも関わらず、演算をそのまま続けることにあります。
したがって、単に出力をリミットするだけでなく、演算そのものを頭打ちにすれば、防止することができます。
◆ アナログの回路では、通常は、演算部分もリミットされており、そのリミット値が出力のリミッタ値にもなっています。
すなわち、通常は、とくに対策をたてなくても、リセットワインドアップ防止回路になっています。
◆ ディジタル制御においては、ベロシティフォームには、リセットワインドアップの現象はありません。
ベロシティフォームの制御演算は、実行し続けます。しかしその出力は、前回出力との差分です。
この出力を、カウンタで受けてカウントします。このカウンタの桁数は有限であり、それがリミッタ特性になっています。
演算部からは、値を送り続けますが、カウンタがリミットに達すると、演算部から送られた値は無視され、切り捨てられます。
すなわち、操作部のカウンタを総合して考えると、演算は頭打ちになっています。
ただし、カウンタの出力範囲が、アクチュエータの出力範囲よりも大きいと、リセットワインドアップの原因になります。この点に注意する必要があります。
◆ ポジションフォームは、対策を講じないと、リセットワインドアップが発生します。
制御演算式の中で、演算の切捨てを行なう必要があります。切捨て処理の具体例を以下に示します。
PI 動作においては、式 2c で、計算された演算結果の yi がリミット値をオーバーする条件のとき、出力 yi の値がリミット値になるように、積分レジスタの値を逆算して、その値を積分レジスタに書き込みます。
そして、出力値は、リミット値にします。
PID動作のときも、PI 動作の部分で、上記の処理、すなわち、積分レジスタの値を逆算して、その値を積分レジスタに書き込むことを行ないます。
このとき、微分部分の演算を行ないません。
その後に、微分部分の演算を行ないます。
前記の積分部分の演算と、微分部分の演算を総合した結果がリミット値を越えているときは、リミット値を出力値にします。
リミット値を超えていないときは、その演算結果を出力します。
実用式のときは、演算式自体が、PI 動作部と PD 動作部とに分かれていますから、単純に PI 動作、PD 動作と演算を進めれば良い訳です。
◆ リセットワインドアップ防止機能付きコントローラのサブサーキット PIDAW を用意しました。アナログ制御の周波数領域形のサブサーキット PIDA にリセットワインドアップ防止回路を付け加えたものです。
微分先行形と同様に、アナログモデルで、ディジタル制御の実用式に対応することができるモデルです。
[注]
PIDA は、伝達関数を使用しています。伝達関数では、非線形を作れません。
したがって、アナログの電子回路そのままを、シミュレーションモデルにしています。
元になる演算式は同じですが、プログラムは全面的に変更されています。
アナログの電子回路になじみが無いと、分かりにくいかも知れませんが、プログラムには、十分にコメントを付けてありますから、興味のある人は、たどって見て下さい。
◆ リセットワインドアップ防止回路は、アナログの PID 制御で使われている方式ではなく、5.5.(3-B-c)に示したディジタル方式のやりかたになっています。
書式は、
* 出力 目標値 制御変数 比例 積分 微分 上限 下限 .SUBCKT PIDAW CNOT SP PV PARAMS: KP=1 TI=1MEG TD=0 VU=1MEG VL=-1MEG
で、CNOT、SP、PV、KP、TI、TDは、PIDA と同じです。
それに、リミッタのリミット値VU(上限)とVL(下限)が加わっています。サブサーキットLIMITと同様にデフォルトは、1MEGと-1MEGです。
[注] リミッタが働かなければ、PIDA と同じに動作します。PIDA を使用しないで、全て PIDAW を使用しても、差し支えありません。
◆ サブサーキット PIDAW を使用して、シミュレーションを行います(図 5-29)。制御対象は、図 5-27と同じです。
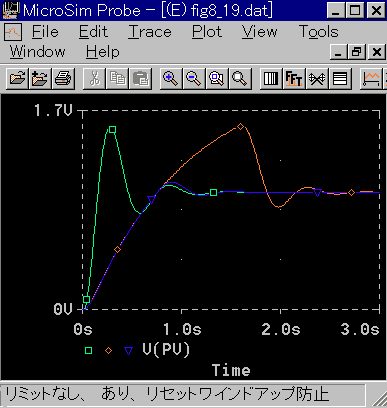
◆ 出力に制限が無いときに比べて、出力制限によって、応答が遅くなっています。これはやむを得ないことです。
しかし、リセットワインドアップが無くなっていますから、その分応答が大幅に改善されています。