◆ D 動作単独の制御演算式は、
・・・・・ (3-2-12)
です。ここで TD は微分時間です。オフセット EFD は、3.2.4.(1-A)式 3-2-6、7 から、
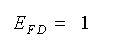・・・・・ (3-2-13)
です。
◆ これは無制御と同じですから、制御能力がないことを意味します。したがって、P 動作を補足する形で PD 動作として、また PI 動作を補足して PID 動作として使用します。
PD 動作、PID 動作として使用する場合も、元の P 動作、PI 動作のオフセットには影響を与えません。
◆ D 動作の効能は、制御応答を改善し、速くすることです。PD 動作 (1 次遅れフィルタなし) の周波数応答を図 3-2-40 に示します。
[図 3-2-40] PD 動作 (フィルタなし) の周波数応答
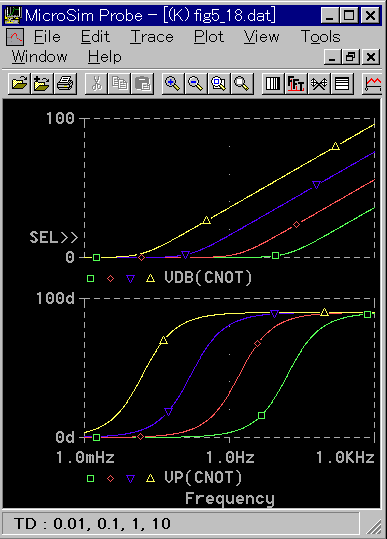
◆ 微分は積分の逆演算ですから、その性質も積分とちょうど逆になります。微分動作の効能は、位相に現われています。
位相を進めますから、一巡伝達関数の位相遅れを減らします。したがって、安定限界の周波数が高くなり、制御応答が速くなります。
ただし、その副作用として高周波における増幅率が高くなります。このことが、3.1.3.(5-B-b) で説明したように、障害となります。対策として 1 次遅れフィルタを併用したものが、実用されている式です。
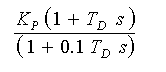・・・・・ (3-2-14)
図 3-2-41に周波数応答を示します。
[図 3-2-41] フィルタを用いた実用の PD 動作の周波数応答
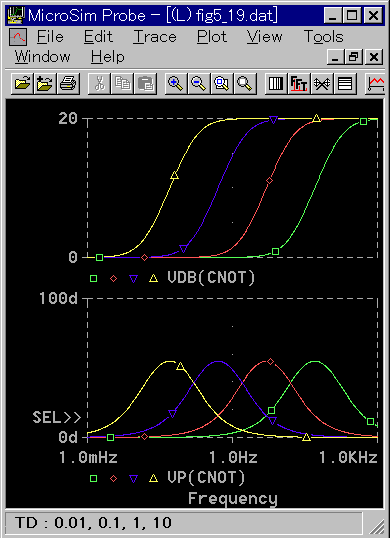
◆ フィルタのおかげで副作用が減り、高周波の増幅率は 20 dBで頭打ちになります。ただし効能の方も減り、90°の位相進みは約 55°に抑えられてしまいます。すなわち、副作用を抑えるために、効能を若干犠牲にしたことになります。
制御に適用したときの、一巡伝達関数の改善とステップ応答による効果を、図 3-2-42、図 3-2-43 に示します。
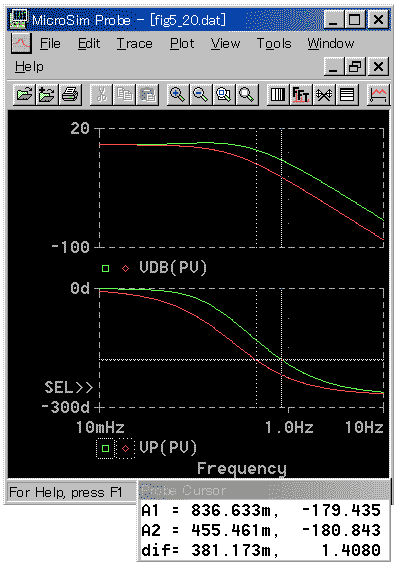
◆ 位相が改善されます。安定限界における周波数は、P 動作の455mHz が、PD 動作では、836mHz になりますから、かなりの改善です。
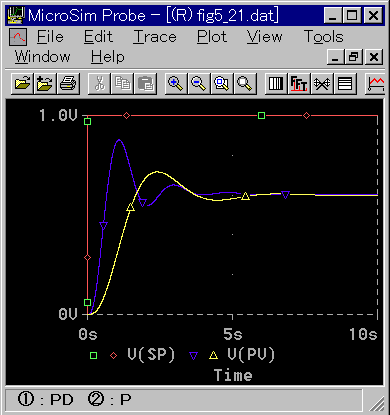
◆ P 動作の応答は、かなり緩くなっています。これは、P 動作単独の比例ゲインKP を、PD 動作のときの値と同じにして比較したためです。P 動作単独の応答は、改善可能です。
PD 動作は、図からも分かるように,オフセットがあります。D 動作の効果は大きいのですが、この点で、用途に制約があります。
また、フィルタによって副作用を抑えたとは言っても、副作用が無くなったわけではありません。ノイズが比較的大きな制御対象では、ノイズによる影響を無視することは、できません。D 動作を効かせることが、困難な場合があります。
[ケース・スタディ 3-2-2]
★ PI 動作のときと同様に、制御対象の特性を変えてケース・スタディしてください。
◆ オフセットもなくしたい、制御応答もできるだけ速くしたい、この両方を同時に満たすためには、PID 動作を使用します。
PID 動作では、I 動作の副作用である遅れの増加は、D 動作によって補われます。しかし、D 動作による副作用は、PD 動作と変わりありません。
PID 動作の制御演算式は、一般に、1.6.(1) の式 1-2 に示したものと、されています。これを伝達関数で表わすと、
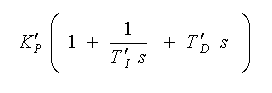・・・・ (3-2-15)
となります。この式も実際によく使用されている式です。この式を「時間領域形 」と呼ぶことにします。
◆ しかし実際に良く使われている式が、もう一つあります。
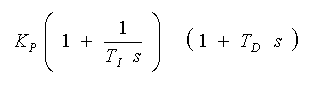・・・・ (3-2-16)
です。これを「周波数領域形 」と呼びことにします。
時間領域形と、式の形は異なりますが、実質的な内容は同じです。すなわち、式 3-2-16 を変形すると
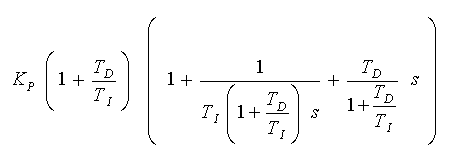・・・・ (3-2-17)
となります。この式と、式 3-2-15 から、両式の制御パラメータを比較すると、
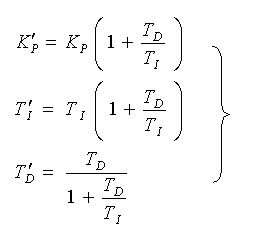・・・・ (3-2-18)
の関係があり、相互に換算することが可能です。
◆ 両式とも微分を含んでいますから、実用するためには、副作用を減らすための、1 次遅れフィルタが必要です。これを加えると、時間領域形は、
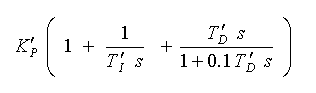・・・・ (3-2-19)
または、
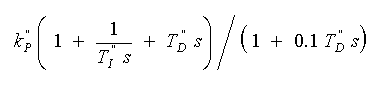・・・・ (3-2-20)
の2つが考えられます。
しかし、この両者の周波数応答は、ほとんど一致し、実用上の差は全くありません(図 3-2-44)。曲線は、ごく一部を除いて、完全に重なり合っています。
[図 3-2-44] 式 3-2-19 と式 3-2-20 の比較
◆ どちらでも良いのですが、この講座では、式 3-2-19 を使用します。
周波数領域形は、
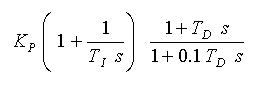・・・・ (3-2-21)
です。
周波数領域形はサブサーキット、PIDAに、時間領域形(式 3-2-18)はサブサーキットPIDJになっています。PIDJもライブラリcont.libに入っています。
◆ フィルタを含まない元の式は、相互に換算が可能です。しかし、フィルタを含む実用式では、上記のようにフィルタ特性が異なるので、両式の特性を完全に一致させる換算は不可能です。
ただし、式3-2-17の換算式から分かるように、TD / TI の値が小さければ、両者の差は少なく、換算の必要もありません。
具体的に、どの程度の差があるのかを、周波数応答で比べて見ます(図 3-2-45、図 3-2-46 )。
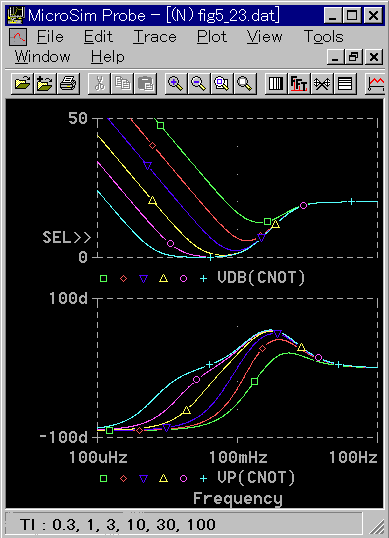
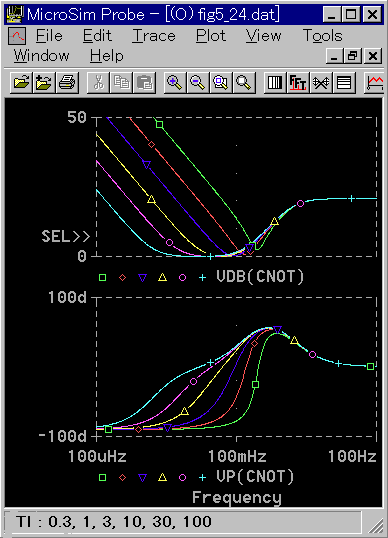
◆ 周波数応答波形は、微分時間TDと積分時間TIとの比によって変化します。図は、比例ゲインを 1 、微分時間 TD を 1 に固定して積分時間 TI を変えています。
TI > 3 の範囲では、両者は一致してると、見なせそうです。これを図 3-2-47で、さらに確認します。
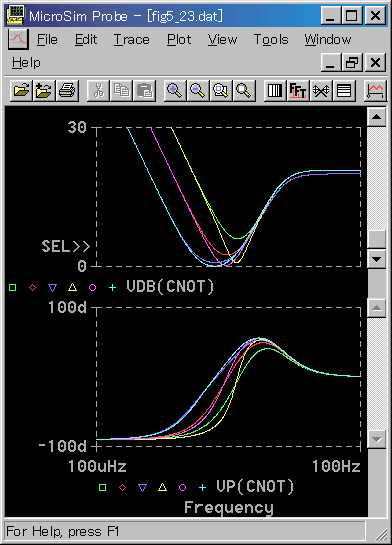
◆ 周波数領域形と時間領域形は、(TD / TI) > 1、(TI < 1)の範囲では、かなり特性の差があります。しかし、この範囲は、制御がうまく行かないので、非実用範囲です。
実際の制御に使用されているのは、(TD / TI) < 0.3、(TI > 3)の範囲です。このうち、(TD / TI) < 0.1、(TI > 10)では、よく一致しています。
(TD / TI) = 0.3、(TI = 3)の近辺では、若干の差があります。通常は無視できる程度の差ですが、この細かい差を考慮した方が良い場合もあります(3.3.2(5)参照)
◆ 解析、設計を進めるとき、パラメータの独立性 ということが、一つの指針になります。
複数のパラメータを持つシステムにおいて、その各パラメータ値は、ある特性値に対応します。たとえば、積分時間 TI は、オフセットを無くす速度を決めます。
このとき、ある一つのパラメータ値は、ある特定の一つの特性値のみを変化させ、他の特性値に対しては、無影響であることが望まれます。このような性質をパラメータの独立性といいます(図 3-2-48)。
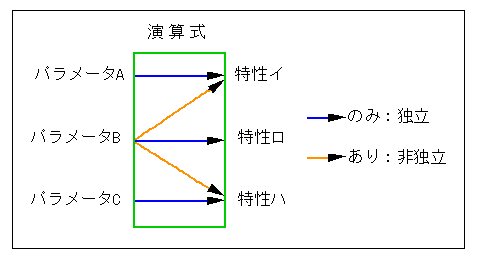
◆ システムの解析、設計を進めるとき、そのパラメータに独立性があることが、望ましいことです。逆に独立性が無く、互いに影響しあうことを、干渉 があるといいます。
さて、時間領域形は、式 3-2-19 からみて、時間領域、たとえばステップ応答において、パラメータの独立性があると考えられます。
周波数領域形は、同様に、式 3-2-21から、周波数応答の上でパラメータの独立性があります(表 3-2-3)。
| - | 時間領域における応答 | 周波数応答 |
| 周波数領域形 | 干渉あり | 独立 |
| 時間領域形 | 独立 | 干渉あり |
◆ ただし、時間領域形と、周波数領域形と、その特性の差が認められない範囲では、実質的には、独立と考えて差し支えありません。そして、どちらの式を使用しても、同じ結果が得られます。
(TD / TI = 0.3) の近辺で、細かい差が問題になる場合を除いては、両者は、同等と見なすことができます。この意味では、どちらの式を使用しても構いません。
一方、解析、設計を進める上で、時間領域で、ものを考えるのか、周波数応答を使って進めるのか、ということがあります。
実際に使用している式が、時間領域形であったとしても、周波数応答を使って解析、設計を進める場合もあるでしょう。その逆もあり得ます。
使っている式が、どちらであっても、解析、設計を進めるときに、どちらをベースにして、ものを考えているか、いうことがポイントです。
実際の制御(われわれが住んでいる世界)は、時間領域です。したがって、最終的には、ステップ応答などで確認することが多いでしょう。
しかし、ステップ応答では、詳細な情報を得られません。この点では、周波数応答が優れてます(3.1.2.(2)参照)。解析、設計の途中では、周波数領域が多く使われるでしょう。
この理由から、この講座では、周波数応答を主体にして、解説しています。したがって、制御演算式としては、周波数領域形を多く使用しています。
ただし、どちらが良いかは、好みや、慣れも大きく影響します。人によって異なります。
◆ PID 動作の制御応答を、PI 動作と比較して見ます(図 3-2-49)。
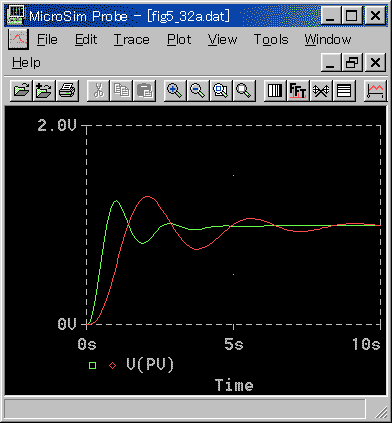
◆ PID 動作、PI 動作、それぞれ、制御パラメータの値を、ほぼ最適にして比較したものです。PI 動作は、応答が遅くなるという副作用があります。それとの比較ですが、D 動作の効果は、かなりあることが分かります。
次に、PID 動作の、目標値変化と、外乱入力に対する応答を比較して見ます(図 3-2-50)。
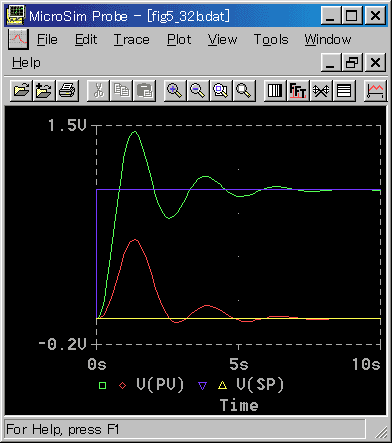
◆ 制御パラメータの値は、目標値変化に対して、ほぼ最適に合わせてあります。制御パラメータの値が等しいときは、外乱入力に対する応答の方が、積分の効きが悪くなっています。
