


◆ 最適調整の手法は多数あります。しかし、この講座では、最適調整については、代表的なものを一つだけ紹介します。この講座で紹介する最適調整の手法は「限界感度法 」です。
この手法は、PI 動作および PID 動作に適用できます。簡単であり、比較的制御対象を乱さないという点で、実用性の高い方法です。
ただし、限界感度法は古い手法ですから、最適解の正確さ、という点では、優れているとはいえません。
最適解の正確さに優れた方式が、多数発表されています。ただし、最適解の正確さは、その手法の優劣を判定する上で、必ずしも、優先度が高い項目ではありません。
最適調整の手法は、その手法が、たまたま、目的とする制御対象にマッチし、適用範囲、適合性も十分得られる場合は、きわめて有効な方法です。
しかし、一般的には、その制御対象に対して、ズバリ、マッチする場合は少ないので、最初に述べたように、「その目的用途に対して最適な解を得ることではなく、それを見出すための目安」として利用することになります。
限界感度法は、この目的に対しては、十分、利用価値があります。
◆ 限界感度法は、実際に制御を行っている状態のままで、簡単な実験を行います。そして実験で得られたデータから、簡単な表を引くことによって、PID のパラメータが得られます。
限界感度法は、自動化やマイコンの時代以前に発表された手法です。全手動の操作において、手間を省く工夫がされています。
限界感度法の実験環境を、図 3-3-4に示します。
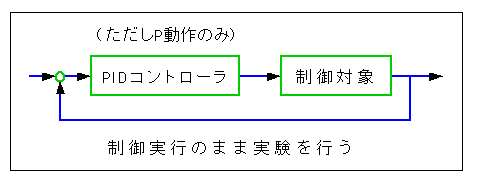
◆ 既に、制御対象を PID 制御している場合は、制御動作を P 動作だけに切り替えます。
P 動作だけはあっても、制御を続行した状態で実験を行うことができます。制御対象を乱さないという点では、制御を停止して実験を行う方式に比べて有利です。
手順の概要を、図 3-3-5 に示します。

◆ 実験は、P 動作だけの制御状態で行います。I 動作や D 動作を使用しているときは、その動作を殺して実験します。
P 動作だけに切り替えたとき、通常は安定なはずです。もし安定でなければ、比例ゲイン KP を小さくして、系を安定にします。
◆ つぎに、比例ゲイン KP の値を少しづつ増加させます。
◆ KP の値を大きくすると、系の安定度が低下します。はじめ非振動的なときは振動的になります。振動的なときは、減衰率が小さくなります(図 3-3-6 の緑〜黄)。
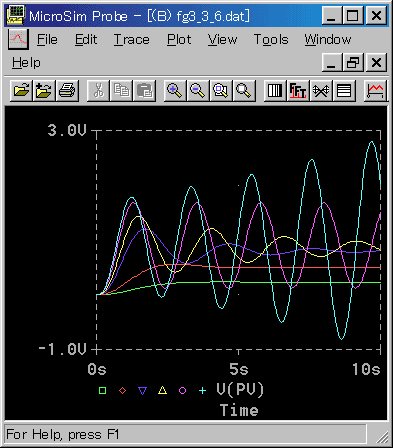
◆ そして、ついに持続振動の状態(図の藤色)になります。KP の値をさらに大きくすると振動が発散し不安定になります(図の水色)。ただし、実験は持続振動になったら終りです。不安定な状態にまで、持ってゆく必要はありません。この意味では、安全性の高い手法ですが、実際の制御対象で実験しているときは、慎重に進める必要があります。
心配なら、真の持続振動まで持って行かないで、その少し手前の、若干振動が減衰している状態に止めて、データを採取します。
◆ 持続振動の状態で、その時の比例ゲインの値 Ku を記録し、振動の周期 Tu を測定します。Ku を限界感度 、Tu を限界周期 と呼びます。
◆ 上記によって得られた限界感度 Ku と限界周期 Tu から、表 3-3-1 によって、最適な比例ゲインKm、最適な積分時間TIm、最適な微分時間TDmを求めます。
| 動作 | Km | TIm | TDm |
| PI | 0.45Ku | 0.83Tu | - |
| PID(時間領域形) | 0.6 Ku | 0.5 Tu | 0.125Tu |
| PID(周波数領域形) | 0.5 Ku | 0.5 Tu | 0.16 Tu |
[注]
限界感度法の表は、元々は、時間領域形用に作られたものです(表の PI と PID (時間領域形)。
これを周波数領域形用にモディファイしたものを追加してあります( PID (周波数領域形))。追加した理由は3.3.2.(5)で説明します。
◆ 限界感度法は、適合性に関しては十分に優れているとは言えません。
また、最適な応答波形は、本来は、制御対象によって異なります。これらの要因から、通常は、さらにトライアルを行うことが、必要になります。
ただし、3.2.1.(1)に述べたように、必要とする制御成績が得られればそれで充分な訳ですから、余計な手間をかけて、トライアルを進める必要はありません。
◆ 実験に際しての注意事項を示します。
◆ 限界感度法のベースになっている制御理論では、制御系は線形であることを前提としています。実際の系の多くは非線形です。
線形とは、一口に言えば、入力と出力との関係が,直線で表されるということです(図 3-3-7)。
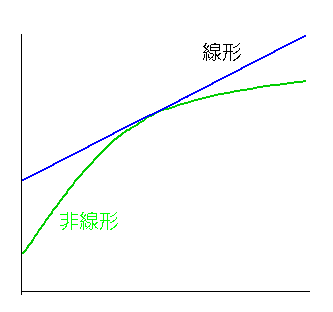
◆ 非線形は、直線では表せないものです(たとえば図ように曲線となるもの)。
非線形系は、理論的な取り扱いが、非常に難しいのです。このため、非線形系は、線形で近似して取り扱います(図の曲線の場合は、その曲線に対する接線で近似)。
しかし近似ですから、線形では説明できない現象が起こります。
系が線形であれば、持続振動を起こす比例ゲイン Ku は唯一です。
しかし系が非線形であると、持続振動はある範囲を持ち、その範囲内の比例ゲインで、持続振動となることがあります。そのような場合には、一般に、比例ゲインを大きくするにつれて、持続振動の振幅が増加します。
このような場合でも、実験は、持続振動を起こす最低の比例ゲインで止めて差し支えありません。振幅の増大を確認する必要はありません。
◆ 減衰振動を含めて、振動する条件が成立していても、振動のキッカケがないと、振動は発生しません。通常は系に常時存在するノイズが、このキッカケになり、振動を起こします。
しかし、ノイズが少ない系では、振動する条件になっていても、振動が起こらないことがあります。
この状態が起こると、振動の条件になっているにもかかわらず振動しないので、比例ゲインを大きくして行くことになります。
このような状態のときは、何かのキッカケで、突如、不安定になることが、あります。このような場合には、制御対象に、大きな影響を及ぼします。実験に危険が伴う恐れすらあります。
これを防ぐために、比例ゲインを大きくするたびに故意に振動のキッカケを作ってやると、安全に、かつうまく行きます。振動のキッカケは、たとえば、目標値をパルス状に一時的に変化させることによって作ります(図 3-3-8)。
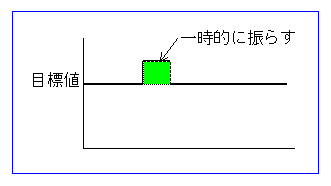
◆ パルスのパワー (図の緑色の面積) は、振動を引き起こすのに十分な範囲で、なるべく小さくします。
◆ 限界感度法は、P 動作における安定限界を求めていることになります。
制御系の解析、設計のためには、安定限界付近の周波数応答が重要です。簡単な実験という前提から、周波数応答波形を求める代わりに、最も重要な1点である、安定限界を実測している訳です。
この意味で、非常に優れた実験です。
◆ 標準Kの制御対象に、限界感度法を適用して、限界感度法による最適条件(Km、TIm、TDm)を求めて、そのパラメータを設定したコントローラの、周波数応答を、図 3-3-9 に示します。求まった限界周期はTu=2.23 (限界周波数fu=0.45)、限界感度はKu=8.9です。
[図 3-3-9] 最適条件におけるコントローラの周波数応答
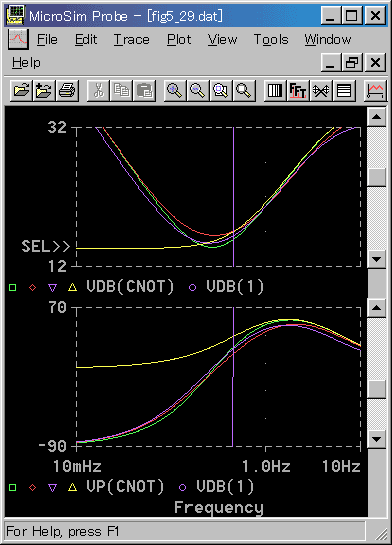
| コントローラ | 適用パラメータ | |
| 緑 : | 時間領域形 | 時間領域形 |
| 赤 : | 周波数領域形 | 時間領域形 |
| 青 : | 周波数領域形 | 周波数領域形 |
| 黄 : | PD 動作(比較用) | |
◆ 図で、コントローラは、使用したコントローラの、制御演算式のタイプです。適用パラメータは、表 3-3-1 のどれを適用したかを示します。
比較のために、PD動作(実用)「黄」を入れてあります。また、縦線は限界周波数(安定限界の周波数)です。
コントローラのゲインは谷を作っています。この谷の周波数は、ft=0.28で、限界周波数よりも、若干低いところにあります。
積分動作、微分動作が共に良く効くためには、コントローラの谷は、広い鍋底形よりも、できるだけシャープな谷であることが望まれます。
広い鍋底形だと、一方に最適だと他方の効きが悪くなります。限界感度法は、シャープな谷を作る条件を求めているわけです。
限界感度法で求めた条件は、この要求を満たしています。
◆ 積分動作の効能は、ゲインの立ち上がりです(3.2.4.(2-B))。コントローラの谷の左側は、積分動作の効能、そのものです。
コントローラの谷の右側は、微分動作の副作用です(3.2.4.(3-B))。しかし、図から分かるように、副作用の発生する周波数は、効能の発生する周波数と同じです。
PD 動作と比較すると、副作用は、ほぼ同じです。効能は、若干落ちるようですが、大したマイナスではありません。I 動作が付け加わったことによる、マイナスは少なそうです。
標準 K の制御対象で制御を行った結果(図 3-3-10「緑」)を見ると、良好に制御され、ほぼ最適と思われます。限界感度法が、よく適合していることが分かります。
また、比較のために入れた PI 動作「黄」と比べて、応答が速くなり、D 動作の効果が現われています。
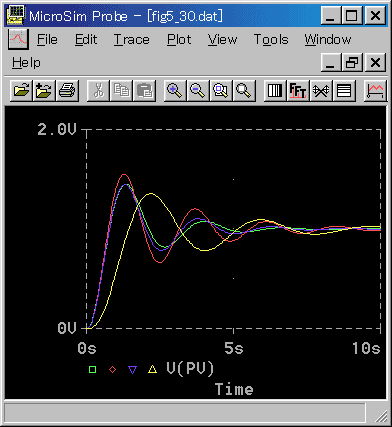
| コントローラ | 適用パラメータ | |
| 緑 : | 時間領域形 | 時間領域形 |
| 赤 : | 周波数領域形 | 時間領域形 |
| 青 : | 周波数領域形 | 周波数領域形 |
| 黄 : | PI 動作(比較用) | |
◆ 周波数領域形のコントローラで、時間領域形と同じパラメータ値を使用したときの周波数応答は、図 3-3-9 の「赤」です。時間領域形「緑」と、かなり良く一致しています。
しかし、制御応答(図 3-3-10「赤」)を見ると、かなり振動的になっています。これは、パラメータ値が、TD / TI = 0.25 であり、3.2.4.(4-B)の図 3-2-47に示した TD /TI = 0.3 に近いからです。
すなわち、ゲインの谷が、周波数領域形の方が高くなり、コントローラの比例ゲインKPを高くしたのと等価になっているのです。
この程度の応答の違いは、元々の限界感度法の適合性から考えても、無視しても差し支えない程度です。最適調整が、トライアルの出発点であることを考えれば、実用上の問題はありません。
◆ ただし、解がより振動的な方向になるということは、余り好ましいことではありません。適合性が悪いとき、非振動的な方向になることは安全サイドです。しかし、振動的になることは、危険な方向です。
この意味で、周波数領域形用に修正した限界感度法の表を、もう一つ別に作ることにしました。修正のついでに、結果として、時間領域形とステップ応答の波形が、ほぼ一致するように表の値を決めました。
これが表 3-3-1の周波数領域形です。このときの応答が、図 3-3-9と図 3-3-10の「青」です。時間領域形の応答と、良く一致していることが分かります。
★ フィードバック制御では、実際の制御、シミュレーション 共に、トライアルを多く使用します。限界感度法も、最終結果を一発で求めるのでは、ありませんから、トライアルを伴います。
PSPICE では、.STEP コマンドを利用すれば、効率よく、トライアルを行うことができます。さらに、1 つの回路ファイル内に独立した複数の回路を作る方法を利用することもできます(2.2.7.(2))。
★ 実機でトライアルを行う場合に、予め、シミュレーションによるトライアルを行っておくことが、有効です。
トライアルを、効率よく行うには、
(a) 適切なトライアルの出発点
(b) 適切なトライアルのステップ幅
が重要です。
★ 制御パラメータのチューニングでは、限界感度法が、上記 (a) に有効です。
トライアルのステップ幅は、疎調整と微調整とに分けて考えると、効率よくトライアルを行うことができます。
制御パラメータのチューニングにおいては、実用上、ルート 2 刻みが微調整として使用されます。すなわち、1.4 (1.5) 倍または、0.7 倍します。
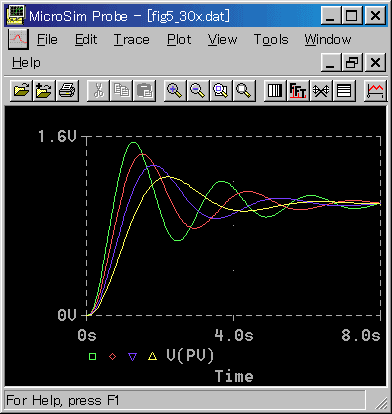
★ 図は、ルート 2 刻みで、比例ゲイン KP を変化させた、制御応答の見本です。
通常は、このルート 2 刻みで十分ですが、とくに精密に調整するときは、必要に応じて、さらに細かくトライアルします。
この講座では、通常は微調整に、ルート 2 刻みを使用しています。
★ トライアルは、トライアルする変数が 1つのときは、簡単です。変数が 2つになっても、実用の範囲です。しかし、変数が 3 以上になると、手間が掛かり過ぎます。
P 動作、PI 動作では問題ありませんが、PID 動作ででは、パラメータが 3つあります。効率よくトライアルする工夫が必要です。
★ その 1つの方法として、積分時間 TI と微分時間 TD とを、連動させる方法があります。図 3-3-9 に示したように、最適条件では、周波数応答が適切な谷を作っています。この条件は、TI / TD = 4 です(表 3-3-1)。
この事実を利用して、TI / TD = 4 に固定し、連動させてトライアルを実行します。
★ 通常は、この方法で、最適条件が求まります。このときも、通常は、ルート 2 刻みで十分です。最適条件に近いところでは、評価関数の値は、十分に細かくなります。
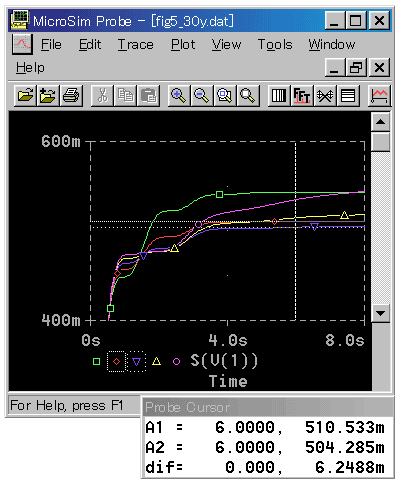
★ 図は、TI / TD = 4 で TI をルート 2 刻みで変化させたときの、評価関数の値です。最適値から隔たったところでは、大きく変化していますが、最適値の付近では、小さく(1% 程度)変化していることが分かります。
★ 図 3-3-9 では、縦の補助線が入っています。
横の補助線は、PROBE 画面で、定数を出力させれば良いので簡単です。PROBE 画面で、TRACE ADD で、TRACE EXPRESSION 欄に値だけを書き込んで作ることができます。
また、予め回路ファイルでデバイス電圧源を使用して一定電圧を作って置くことよっても可能です。
★ これに対して縦の補助線を作るのは面倒です。通常はカーソルを利用する方が簡単です。しかし、体裁を良くするために、縦の補助線も作ることができます。これは、予め回路ファイルで作製しておきます。
(A) トランジェント解析の画面に作る
トランジェント解析では、電圧源の折れ線近似波形を利用します。この書式は、
V<名称<+ノード><-ノード> PWL(<t1><v1><t2><v2>・・・<tn><vn>)
( < > は、必須)
です。各値の間は、スペース、コンマ、(、)、等を挿入します。指定した点 <ti><vi> を結ぶ折れ線を作ります。
★ 縦の補助線は折れ点を2点指定します。すなわち、 PWL(T,V1)(T+,V2) とします。
ここで T は、補助線を入れる時刻、T+ は、補助線を入れる時刻に、ごくわずかな値を加えたものです。V1 と V2 は、補助線の下と上の値です。PROBE 画面の外側にはみ出すように、値を決めます。
最初 PROBE 画面には、補助線の下と上の線が表示されますから、縦軸を編集して画面の外に追い出します。
(B) AC 解析の画面に作る
AC 解析は、やや、面倒ですが、アナログ・ビへービア・モデルの周波数テーブルによって作ることができます。
★ この周波数テーブルのモデルは、任意の周波数応答波形作るためのものです。実験で求めた周波数特性を使ってシミュレーションを行うのに利用します。書式は、
E<名称><+ノード><-ノード>FREQ {式} =<<周波数値>,<振幅値>,<位相値>>*
( < > は、必須 [ ] は、省略可能 * は、繰り返し可能)
で、周波数値は、最小から最大値へ小さい順に並べます。
★ このモデルを利用して、横および縦の補助線を作ります。横の補助線の書式は、
FREQ {V(IN)} = (F1,G,P)(F2,G,P)
で、IN は、AC 解析の入力電圧のノードです。F1、F2 は周波数範囲で、.AC で指定した周波数範囲よりも広く取ります。G はゲインの横線の位置で、単位は dB とします。
★ P は位相の横線の位置で単位は度です。縦の補助線の書式は、
FREQ {V(IN)} = (F,X1,Y)(F+,X2,Y)
です。F、F+ は、縦線の周波数で、記号の意味と使い方は、トランジェント解析と同じです。X1 と X2 は、補助線の下と上の値です。
★ 下の値は、ゲインの下の dB 値と、位相の下の度の値との両方を下回る値とし、上の値は、ゲインの上の値と、位相の上の値との両方を上回る値にします。
★ Y は使用しませんから、エラーにならない範囲の適当な値(通常はゼロ)を入れておきます。
★ PROBE 画面に出力するときは、ゲインだけでなく位相の方も、VDB を使用します。まともに位相を利用すると、PSPICE は、勝手に360°を加減算してしまうので、うまく行かないことがあります。
(C) 見本の回路ファイル
なお、これらの見本の回路ファイル HOJOSEN.CIR を入れてありますから、利用してください。
◆ 限界感度テスト用のプログラム LMTSMTST.CIR と LMTMTSF.CIR を用意しました。
◆ LMTSMTST.CIR は、制御対象を所定のものに入れ替えて使用します。限界感度法のやりかたを、そのまま行なうプログラムです。したがってトライアルが必要です。
シミュレーションですから、ステップ応答を使用しています。限界感度法を理解するためのケーススタディ用です。
◆ LMTSMTSF.CIR も、制御対象を所定のものに入れ替えて使用します。限界感度法は使用しないで、直接制御対象の安定限界を求めます。したがって、トライアル無しに一発で求まります。実際には、こちらを使用するのが便利でしょう。
周波数応答のPROBE画面は、位相については、通常通り、VP(PV) を表示します。ゲインは、dB 表示にしないで、リニアスケール V(PV) とし、その逆数 1/V(PV) を表示させます。
先ず、周波数応答の位相 (VP(PV)) が、-180°の周波数 fu を求めます。この逆数 1/fu が限界周期 Tu です。
◆ 次に、この限界周波数 fu における、1/V(PV) を求めます。この値が、直接限界感度 Ku です。
正確な値を求める必要がある場合は、コラム 3-3-3 を参照してください。
標準および標準 K の制御対象で、LMTSMTST.CIR によるテストを行なった結果を、表 3-3-2 に示します。
| - | 限界感度(KU) | 限界周期(TU) |
| 標準 | 23.8 | 0.58 |
| 標準K | 8.9 | 2.23 |
[ケース・スタディ 3-3-1]
★ 制御対象の特性をパラメータによって変更し、その制御対象の限界感度/限界周期を LMSMTST.CIR によってもとめ、次いで LMSMTSF.CIR を使って比較してください。
★ シミュレーションで作成した制御対象の、限界周期と限界感度は、回路ファイル LMTSMTSF.CIR を使用して、求めることができます。
概略値で差し支えなければ簡単ですが、正確な値を求めるのは、工夫が必要です。
また、その他にも、カーソルを正確に合わせて、正確な値を読み取ることが必要な場合があります。
★ このようなときには、手動でカーソルを合わせるのでは無く、カーソルコマンドを使用します。
「Tools」→「Cursol」→「Display」 とクリックして、カーソルを表示させた後に、再び 「Tools」→「Cursol」 とクリックすると、今度は幾つかのコマンドが表示されます。
Peak : 次のピークへ移動
Trough : 次の谷へ移動
SLope : 次の最も急なスロープへ移動
Min : y軸の最小値へ移動
Max : y軸の最大値へ移動
で、これらの正確な位置に移動します。
★ また、
Search_Commands
で、値を記入して、その値のところに、移動させることができます。
SXV(<値>) : <値>で指定したx軸の値を持つ最も近い位置を探します。
SLE(<値>) : y軸が<値>を通過する位置を探します。
回路ファイル LMTSMTSF.CIR で限界周期 fu と、限界感度 Ku を求めるときは、Search_Commands を使用します。
★ 先ず、周波数応答の位相 VP(PV) にカーソルを置き、Search_Commands で、
SLE(-180)
として、カーソルを-180°のところに移し、限界周波数 fu を求めます(下図の例では、450.197m)。
★ 次に、カーソルを、ゲイン側 (表示は、1/V(PV) )に移します。そして、Search_Commands で、
SXV(<fu値>) 下図の例では SXV(450.197m)
とすれば、限界感度 Ku (下図の例では、9.0038 )が求まります。
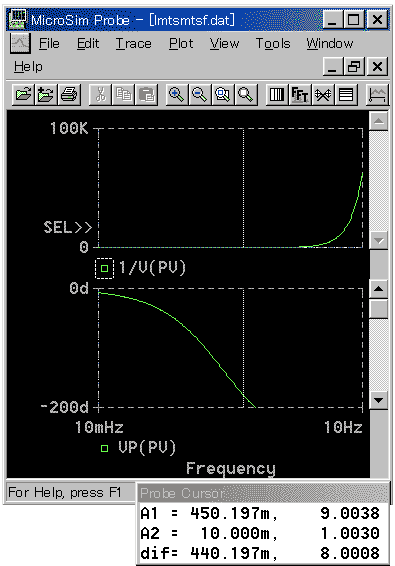
★ 図は、既に限界周波数 fu を求め終わり、限界感度 Ku を求めている画面です。
1/V(PU) は、図の上では、ゼロの水平線です。しかし、PSPIC の内部では、浮動小数点演算を行っています。表示された数値は、十分な精度があります。