


◆ 限界感度法の適合性と適用範囲について検討します。制御対象は、1 次遅れ + むだ時間(サブサーキット PRMF )を使用します。
1 次遅れの時定数を T 、むだ時間を L とすれば、その比 L/T の値は、制御の難しさを表します。L/T が大きいほど、制御が難しい制御対象です。
L/T によって、限界感度法の適合性と適用範囲が、どのようなるかを調べます。L/T による、制御成績の変化も分かります。
◆ 限界感度法の適合性を比較して見ます。
先ず PI 動作について、図 3-3-11、図 3-3-12 に示します。
[図 3-3-11] L/T による限界感度法の適合性( PI 動作)−1
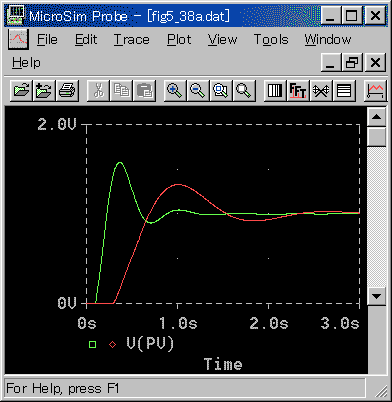
[図 3-3-12] L/T による限界感度法の適合性( PI 動作)−2
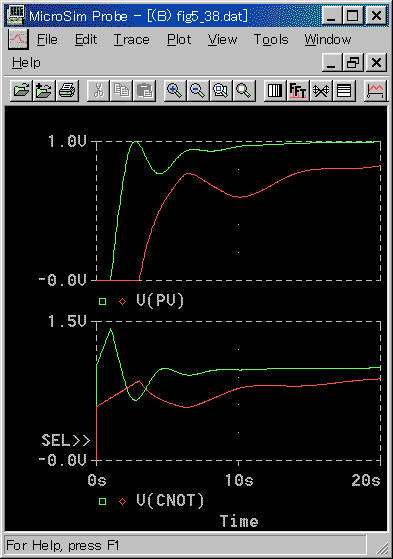
◆ 図では、L/T は、T 固定で L を変えています。L/T が大きいと、遅れ自体も大きくなっています。また、L/T が大きいと適合性が悪くなります。PI 動作の場合には、適合性は、振動の減衰率よりも、積分動作の効きに大きく現われています。
制御応答を詳しく調べるために、操作出力 CNOT も表示しています。
[注] 制御応答を改善するなどの目的で、制御応答を、詳しく解析したいときがあります。このようなとき、制御変数だけでなく、操作出力を調べることは、大きな効果があります。
最初のステップで、偏差もステップ状に大きくなり、操作出力もステップ状に変化しています。このときの出力値は、P 動作による分です。
操作出力 CNOT が変化しても、むだ時間のために、制御変数 PV は変化しませんから、偏差が大きい状態が継続します。この間 I 動作が働くので、操作出力 CNOT は増加します。
むだ時間を経過すると、制御変数 PV が変化し始め、以降通常の制御動作に入ります。正常動作といっても、むだ時間が存在しますから、その遅れを含んだ動作です。
この応答では、限界感度法によって設定した積分時間が、適正値よりも大きい、すなわち、積分が不足しているので、積分による行き過ぎは発生していません。しかし積分を効かせると、むだ時間による最初の積分効果が、過剰に効いてくる可能性があります。
◆ 次に、PID 動作を調べてみます。PI 動作では、制御演算式の影響はありませんが、PID 動作では、時間領域形と、周波数領域形とでは、違いがあります。
ここでは、周波数領域形を使用し、限界感度法の表は、周波数領域用を使用しました。
結果的には、時間領域形の制御演算式と、オリジナル(時間領域用)の表を組み合わせても、ほとんど、変わりないはずです。
図 3-3-13、図 3-3-14 に適合性を示します。
[図 3-3-13] L/Tによる限界感度法の適合性(PID動作)−1
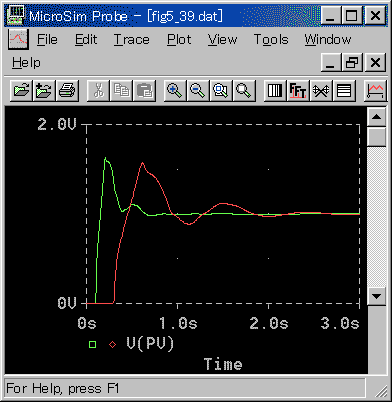
[図 3-3-14] L/Tによる限界感度法の適合性(PID動作)−2
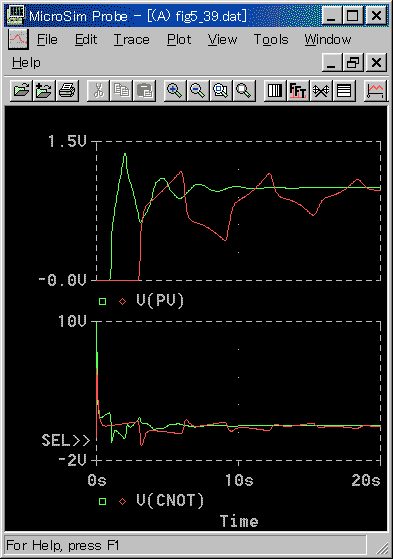
◆ 傾向は、PI 動作と同様です。ただし、適合性の悪さは、PID 動作では、振動の減衰率が小さくなる方向です。しかし、その悪化の度合いは、あまり大きくありません。
この図も、操作出力 CNOT を入れてあります。この図では、微分動作が大きく作用しています。最初のステップで、偏差が急変しますから、操作出力 CNOT に、微分によるパルスが発生しています。
この微分効果によって、むだ時間経過後の制御変数 PV は、非常にシャープに立ち上がっています。このシャープな立ち上がりによって、再び微分が大きく効いて、パルスを作ります。
このパルスが、さらにむだ時間後に、立ち上がっている制御変数を急速に押さえます。その結果、先が尖った応答になります。以降、次第に緩やかになりながら、これを繰り返します。
この波形は、シミュレーションなので、極端に現われています。実際の制御対象は、1 次遅れ + むだ時間で、近似されるのであって、純粋な 1 次遅れ + むだ時間ではありません。
また、操作出力にはリミットがありますから、非常に大きな操作出力は、頭打ちになります(5.5.(2-A)参照)。
[注]
制御対象が、1 次遅れ + 無駄時間のとき、とくに制御動作に D 動作を含むときは、図 3-3-14 に示すように、制御応答が、滑らかではく、角が目立ちます。これは、1 次遅れ + 無駄時間のステップ応答が、無駄時間の後に急に立ち上がっていることが原因です。
しかし、実物の制御対象では、制御応答には、このような角は無く滑らかことがほとんどです。実際の制御対象は、シミュレーションモデルのような、純粋の特性ではありません。各種の遅れが加わっています。これが、制御応答に丸みをつけます。
◆ 以上の、PI 動作と、PID 動作を総合して、適合性を考えてみます。限界感度法を、トライアルの出発点と考えるなら、L/T < 1 は、十分可能であると考えられます。
適合性は、L/T の大きさが、1 以下であれば問題ないと考えられます。
多くの制御対象は、L/T<1 です。限界感度法は、実用上十分な適用範囲があると考えて差支えありません。
ただし、1次遅れ + 無駄時間は、あくまでも近似です。実際の制御対象の適合性が、1次遅れ + 無駄時間よりも悪いこともあります。
◆ 限界感度法は、目標値変化を対象にして、作られています。外乱入力 に対する適合性は、どのようになるのでしょうか。
これを検討する前に、まず、外乱入力一般について、考えてみます。この講座の標準制御対象は、2.2.2.(5)の図 2-2-5 に示した形になっています。
これは、制御対象を 3 次遅れと見なしたときに、最も高い汎用性を持つ形です。すなわち、コントローラの偏差入力と、外乱入力とに対する制御対象特性を、各々独立に、自由に設定可能なモデルです。
一般には、制御系における外乱入力は、図 3-3-15 に示す、2 種類の何れかを使用しています。
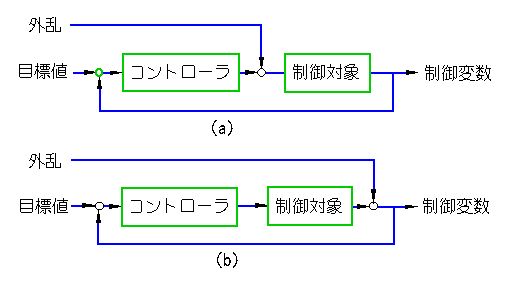
◆ 制御対象が、図のように、1 入力 / 1 出力のシステムであれば、外乱の入力点は、図のように 2 種類しか無いでしょう。
しかし、実際の制御対象は、一般に、もっと複雑であり、多入力 / 多出力のシステムです(3.2.3.(3)参照)。したがって、外乱の入力点は多数あり得ます。外乱が制御変数に与える影響も、それぞれ異なります。
手計算で、制御系の解析、設計を行っていた時代には、とにかく簡単でなければ、なりませんでした。しかし、シミュレーションを前提とした解析、設計では、多少複雑であっても差し支えありません。
何れにしても、外乱の入力点が異なると、制御応答が違ってきます。この講座の標準の制御対象サブサーキット PRCS は、外乱の入力点の相違などに対応できるように、高い汎用性を持たせてあります。
しかし、ここでは、分かりやすいように簡単化して、外乱の入力点は、図のように 2 種類として検討します。
サブサーキット PRMF を使用しますから、偏差入力は、1次遅れ + 無駄時間ですが、外乱入力は、1次遅れです。しかし、外乱入力にむだ時間を含んでいなくても、一般性を失いません。図のモデルの外乱入力は、ループを構成しないからです。
制御要素は、一般に、遅れです。この遅れは、通常は、ローパスフィルタです。ステップ入力は、制御要素を通過すれば、鈍ります。したがって、図 の (b) が最も厳しい条件です。これに対して、(a)は、比較的緩い条件を意味します。
◆ サブサーキット PRMF の 1 次遅れの時定数 TD をゼロと見なせる十分に小さい値にします(真にゼロにすることはできますが、演算時間が長くなります)。
図 3-3-16、図 3-3-17 に、外乱入力に対する、PI 動作の適合性を示します。
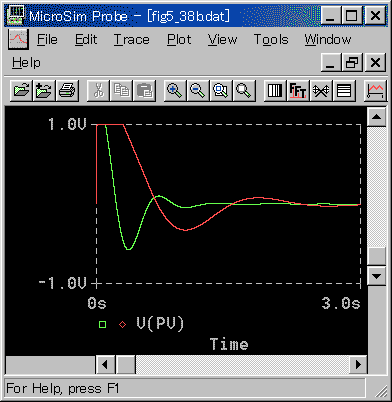
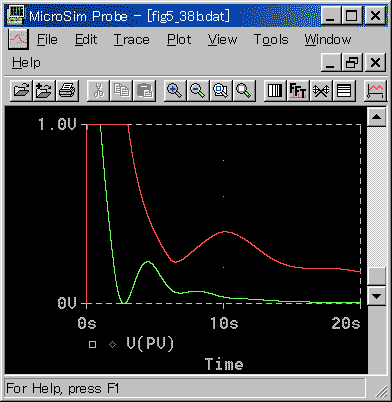
◆ ここで目立つのは、最初の部分で、制御対象の無題時間 L の期間、無制御の状態であり、外乱の影響が,そのまま現われる、ということです。
この現象は、実は、目標値変化のときにも現われています(図 3-3-13、図 3-3-14)。ただ、目標値変化のときは、それが偏差ゼロたっだので、目立たなかっただけです。単に目立たないだけでなく、偏差ゼロですから、評価関数の値にも影響していません。
しかし、外乱入力の場合には、評価関数の値を、著しく悪化させます。むだ時間である以上やむを得ない現象です。
応答波形は、目標値変化と同じ傾向です。したがって、適合性についても、同じになります(3.3.3.(2-A))。
◆ 次に、PID 動作の適合性を示します(図 3-2-18、図 3-2-19 )。
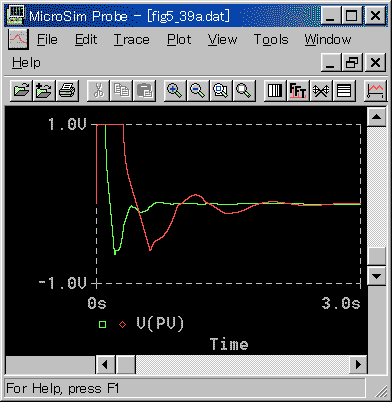
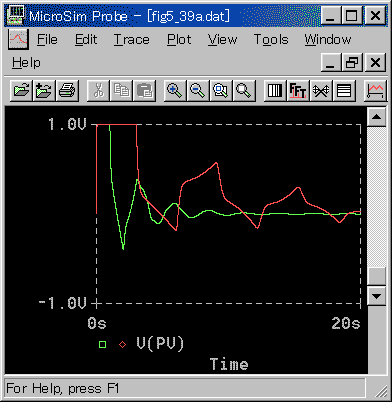
◆ PID 動作についても、PI 動作と同様です(図 3-3-13、図 3-3-14 参照)。
◆ 次に、緩い外乱入力について、図 3-3-20〜図 3-3-23 に示します。比較のために、厳しい外乱入力についても載せてあります。
[図 3-3-20] 外乱入力点による適合性(PI動作)-a
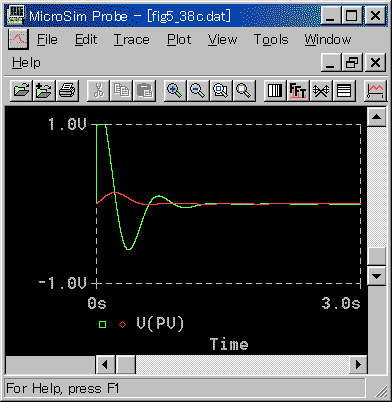
[図 3-3-21] 外乱入力点による適合性(PI動作)-b
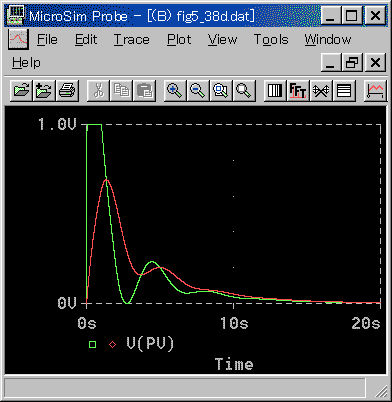
[図 3-3-22] 外乱入力点による適合性(PID動作)-a
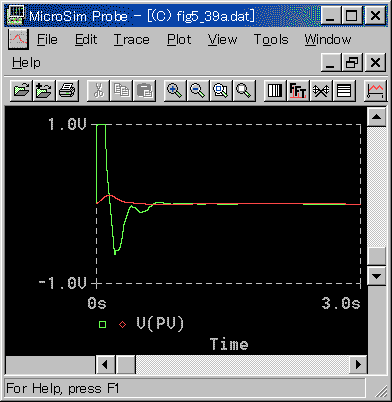
[図 3-3-23] 外乱入力点による適合性(PID動作)-b
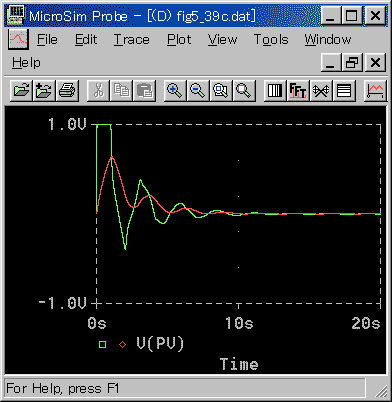
◆ PI動作とPID動作とは、同様な傾向があります。
L / T が小さいとき(図 3-3-20、図 3-3-22)は、相対的に、制御対象の 1 次遅れフィルタ効果が効いて、外乱が打ち消され、偏差は大幅に小さくなります。
L / T が大きくなる(図 3-3-21、図 3-3-23)と、1 次遅れのフィルタ効果が小さく、したがって、厳しい外乱との差が、少なくなります。
フィルタが効けば、その分、評価関数が改善されます。その影響で、適合性も改善されますが、全体的な傾向は変わりません。
◆ 以上、制御対象の特性を 1 次遅れ + むだ時間として、限界感度法の適合性を、検討してきました。
もともと限界感度法は、制御対象を、1 次遅れ + むだ時間であるとして、開発されたものです。したがって、L / T の広い範囲にわたって、良い適合性を有しています。
また、全ての制御対象は、1 次遅れ + むだ時間で近似されます。この意味で、限界感度法は優れています。
ただし、全ての制御対象は、1 次遅れ + むだ時間で近似できますが、全て良好に近似される、ということでは、ありません。かなり近似が荒い範囲もあります。
したがって、限界感度法が、広い範囲で、良い適合性を持っているとは、言い切れません。
◆ 1 次遅れ + むだ時間と異なる制御対象の例として、この講座で使用している、標準 K の制御対象に、限界感度法を使ってみましょう。
図 3-3-24 は、PI 動作、目標値変化です。
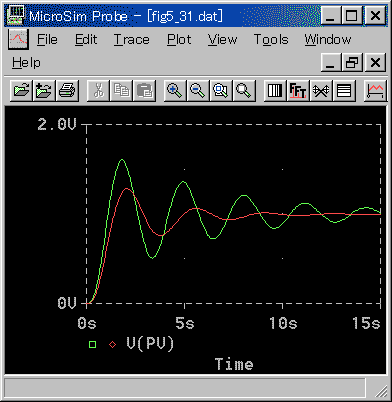
◆ 「緑」は、限界感度法をそのまま適用した波形です。最適な制御応答よりも振動が激し過ぎるようです。
1 次遅れ + むだ時間をベースとした適合性の検討では、PI 動作は、緩すぎる方向でした。このように、制御対象の特性が異なると、適合性に,かなりの差が出ます。
そこで、制御パラメータを若干修正して、減衰率を適正にしたのが、図の「赤」です。
| - | KP | TI | 評価関数の値 |
|---|---|---|---|
| 限界感度法の値 | 4.0 | 1.85 | >1.30 * |
| 修正後の値 | 2.8 | 2.77 | 0.84 |
[注] 評価関数は、2乗誤差面積です。シミュレーション上で、評価関数の値を求める方法は、[コラム 3-2-1]を参照してください。
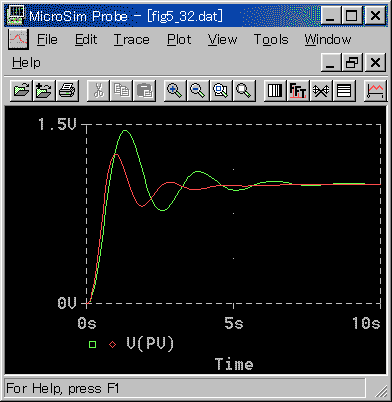
◆ PID 動作、目標値変化の応答波形を図 3-3-25 に、数値を表 3-3-4 に示します。なお、コントローラは周波数領域形で、限界感度法の表も周波数領域形です。
| - | KP | TI | TD | 評価関数の値 |
|---|---|---|---|---|
| 限界感度法の値 | 4.4 | 1.11 | 0.36 | 0.54 |
| 修正後の値 | 4.4 | 2.22 | 0.72 | 0.37 |
◆ 「緑」は、限界感度法そのままです。良好な制御応答波形です。しかし、さらにトライアルすると、評価関数を、さらに、低くすることができます(図の「赤」)。
この例のように、限界感度法そのままで、一見、適正のように見えても、さらに改善できる場合もあるのです。
なお、このトライアルは、積分時間と微分時間との比を一定のまま連動させました。PID 動作は、制御パラメータの数が多いので、まともにトライアルすると、手間が掛かります。連動によって、手間を省きました。
連動させることは、少なくとも、最適条件の付近では、合理性があると考えられます(3.3.2.(5)参照)。ただし、連動させた結果が最適条件であるとは限りません。
◆ 外乱入力に対する応答を示します。制御パラメータの値等は、目標値変化(図 3-3-24、図 3-3-25)と同じです(図 3-3-26、図 3-3-27)。
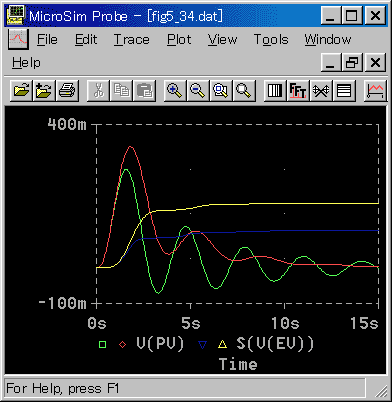
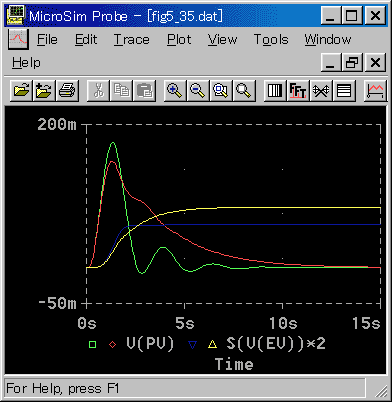
◆ 何れも、制御対象は 3 次遅れですが、外乱の入力点は、図 3-3-15 の(a)と等価です。したがって、外乱の影響は、定性的には、目標値変化に比べて、緩くなる傾向があります。
図には、評価関数の値を入れてあります(S(V(EV))。*2 は、図を見やすくするために、値を 2 倍に表示させたものです。これを見ても分かるように、目標値変化では、改善であった修正が、外乱入力に対しては、改善では無くなっています。
PI 動作の場合には、応答が振動的になることを許容するならば、外乱入力に対しては、比例ゲインを大きくした方が良いことを示しています。
PID 動作では、微分動作の効き方が、目標値変化と、外乱入力とで異なります(5.3.(2-B)参照)