


◆ フィードバック制御の基本は PID 制御です。そして実際にも PID 制御が多く利用されています。PID 制御は、制御演算式が簡単で、その割には、非常に良い制御成績が得られます。しかも使いやすいという特徴があります。
しかし、時代と共に、より良い制御成績への要求が高くなっています。より良い制御を行なうために、PID 制御を改良したり、機能を付け加えたり、複数の制御を組み合わせたりすることも、多く行なわれています。
とくにディジタル制御は、ソフトウェアによって、簡単に機能の付け加えや改造が可能です。
またさらに、より高度な理論に基づいた、PID 制御以外の制御演算も、使用されるようになってきました。
単純な PID 制御に対して、より高度な制御を、アドバンスト制御 といいます(図 5-5)。

◆ 図の、PID 制御の改良、機能の付加も、広義にはアドバンスト制御の範囲に入ります。しかし通常は、さらに高度なものをアドバンスト制御と呼んでいます。
この講座では、高度なアドバンスト制御には触れません。高度なアドバンスト制御を実施するためには、一般に、制御対象の特性を定量的に調べて、それを元にした、制御モデルを作る必要があります。
PID 制御は、制御対象の特性を定量的に把握しないでも、実施すことができます。逆にいうと、このことが、PID 制御の使い易さです。より良い制御を行うためには、それなりの代償が要るということです。
[注] アドバンスト制御については、この章の他に、6.3.2. で、カスケード制御と呼ばれる制御方式を解説しています。
◆ 基本的には PID 制御ですが、制御演算式を、ちょっと変えたものがあります。
その代表的なものが、微分先行形 と呼ばれるものです。
ごく簡単な変形ですが、アナログ制御では、コストアップになります。ディジタル制御なら、ほとんどコストアップ無しに、通常の PID 制御と、この微分先行形とを切り換えて使用できます。
◆ この講座の最初に、フィードバック制御には、定値制御と追値制御の2種類があることを説明しました(1.3.(1)の図 1-6、図 1-7) (図 5-6)。
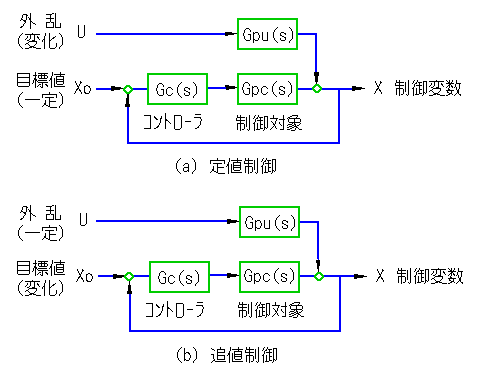
◆ 追値制御は、機械制御の分野で広く使われています。これに対して、プロセス制御の分野では、定値制御が多く使用されています。
追値制御は、目標値を時間とともに変化させます。通常、目標値は連続的に変化します。この目標値の変化に、制御変数を追随させることが目的です。ただし、外乱もありますから、外乱の影響を打ち消す制御も必要です。
定値制御では、目標値は一定です。そして外乱によって制御変数の値が変化してしてしまうのを、制御によっておさえることを目的としています。ただし、目標値が完全に不変であることは少なく、時々目標値を変化させます(1.3.(1-B)の図 1-8)。
同じフィードバック制御であっても、目標値変化と外乱入力とでは、制御応答が異なります(3.2.4.(1-A)の式(3-2-4)と式(3-2-5))。したがって、応答波形も違います(1.6.(5)の図 1-36、図 1-37)。
◆ 微分先行形は、定値制御において、時々目標値をステップ状に変更する場合に有効な制御演算です。
この場合には、目標値変化と、外乱入力との両方に対して、良好な制御が望まれます。しかし、通常の PID 制御では、この要求に対応することができません。
通常の PID 制御を図 5-7 に、微分先行形を図 5-8 に示します。
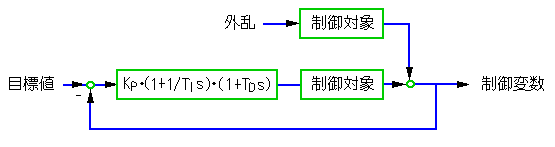
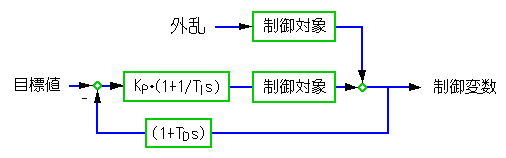
[注] 分かり易くするために、フィルタの式を省略してあります。
◆ 図から分かるように、微分先行形は、1巡伝達関数として眺めると通常の PID 制御ですが、PD 動作の位置が異なります。外乱入力に対しては、微分は、どちらも同様に働きます。
これに対して、目標値変化に対しては、微分の働き方が異なります。
通常の PID 制御では、目標値変化のステップ入力変化が、もろに微分に入り、大きな出力変化をもたらします。
微分先行形では、目標値変化のステップ入力は、先ず制御対象を通過します。制御対象には遅れがありますから、変化速度は遅くなり、それが微分に入力されます。
通常の PID 制御のような、大きな出力変化は起こりません。これが、微分先行形の効果です。
通常の PID 制御では、目標値変化に対する制御応答が過剰になるのを防ぐために、微分を緩くします。このため、外乱に対して微分を有効に働かせることができません。
微分先行形では、外乱に対して、微分を有効に働かせることができます。
◆ 微分先行形は、アナログ・コントローラの製品には、ほとんどありません。ディジタル制御で使用されています。
しかし、シミュレータは、アナログの PIDAF を用意しました。ディジタル制御であっても、サンプリング周期が十分に短いときは、アナログで近似できます。サンプリング周期が長い場合にも、アナログモデルを利用して、シミュレーションを行うことができます(4.2.5.(1))。
サブサーキット PIDAF の使い方は、PIDA と同じです。
◆ 微分先行形のシミュレーションを、行ってみましょう。まず、外乱に対する応答を、検討してみます。
外乱に対する応答は、通常の PID 制御も微分先行形も同じはずです。
これを確認したのが図 5-9 です。
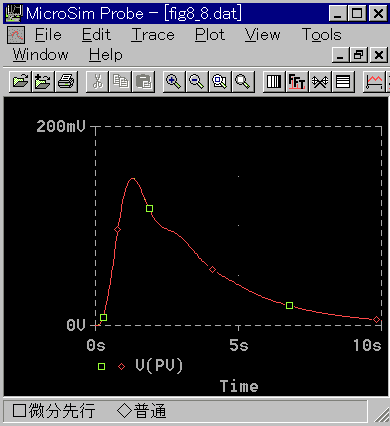
◆ 完全に一致しています。制御対象は標準Kです。限界感度法で求めた値を、目標値入力に対して、修正した PID パラメータを使用しています(3.3.3.(4-B) 表 3-3-4)。
◆ 目標値変化に対する最適パラメータ値ですから、外乱に対しては緩い制御になっています。そこで、比例ゲイン KP 大きくして見ます(図 5-10)。
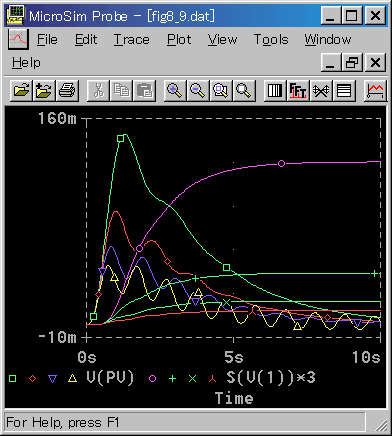
◆ 目標値変化のときに比べると、応答波形が複雑ですから、単純に2 乗誤差面積で評価することは、困難です。
図に示されたような波形であれば、かなり振動的になっても差し支えないことが多いと考えられます。
このような場合には、比例ゲインを、目標値入力に比べて大幅に大きく取ることができます。
目標値入力時の値に対して、比例ゲインを3 倍( KP = 12) にすることは無理かも知れませんが、2 倍 ( KP = 8) なら実用性がありそうです。
◆ 上記の、比例ゲインを大きくした条件では、通常の PID 制御では、目標値入力に対しては使用に耐えません(図 5-11)。
[図 5-11] 通常の PID 制御における目標値入力に対する応答
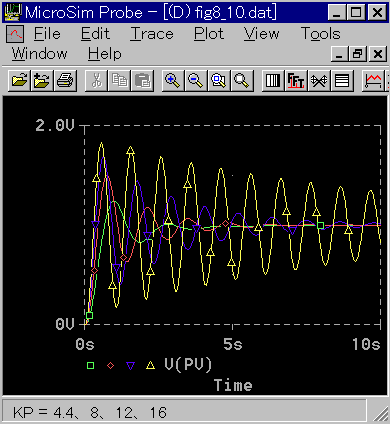
◆ しかし、微分先行形を使用すれば、図 5-12 のようになります。
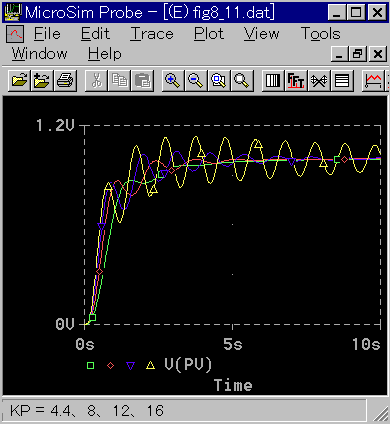
◆ 通常の PID 制御に比べて、立ち上りの応答が遅くなっていることが分かります。したがって大幅な行過ぎを防止します。
しかし、振動の振幅は改善されますが、減衰率は、あまり変わりません。
比例ゲインを通常の PID 制御の 3 倍にすると、振動過多のようです。2 倍なら十分使用可能と思われます。
◆ 以上から、微分先行形は、それなりの効果があることが分かります。しかし、十分な効果というわけには行きません。
その代わり、微分先行形は、通常の PID 制御と同じ手軽さで使うことができます。制御対象の特性を定量的に把握する必要は、ありません。
なお、もっと高度なアドバンスと制御を使用すれば、目標値変化、外乱の両方に対して、それぞれ、最適な応答を得ることができます。