◆ 以上に述べたように、制御系の解析、設計を行うためには、制御対象の周波数応答は、その位相が -180°を過ぎっていることが必要です。
この条件を満足する制御対象モデル は、少なくとも 3次以上の高次遅れか、またはむだ時間を含むモデルでなければなりません。1 次または 2 次のモデルでは、位相が -180°を横切りませんから使用することができません(図 3-2-14)。
[図 3-2-14] 制御対象モデルの候補
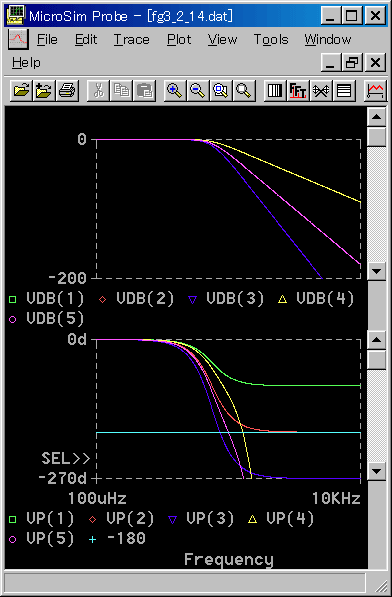
◆ この講座で制御対象のモデルに 3 次遅れを使用しているのは、この理由によります。
従来は、制御対象のモデルとして、2 次遅れモデルが多く使用されていました。手計算の時代には、3 次おくれや、むだ時間は、取り扱いが面倒であり、かつ応答の見通しが良くなかったからです。
2 次遅れは、3.1.3.(2-A)に示したように、、固有角周波数 ON によって応答速度が決まり、減衰係数 ZT によって波形が決まります。式を見ただけで、応答波形を推定することができます。
また、2 次遅れモデルであれば、コントローラに P 動作を使用して、振動的な解を求めることができます。2 次遅れモデルは、十分ではありませんが、手計算の時代には、やむをえないモデルでした。
◆ 制御対象の標準モデルとして、一般に、「1 次遅れ + むだ時間 」が多く使用され、「2 次遅れ + むだ時間」も使われています。
1 次遅れ + むだ時間は、1 次遅れ時定数を T、むだ時間を L として、
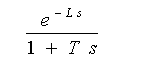・・・・ (3-2-3)
です。比 L/T は、制御対象の制御の難しさを表わします。L/T の値が大きいほど制御が難しい制御対象です。
制御対象 1 次遅れ+むだ時間は、サブサーキット PRMF を用意してあります。ただし 1 次遅れ+むだ時間は操作変数に対してであり、外乱に対しては単なる 1 次遅れです。
* 制御変数 操作変数 外乱 外乱 ゲイン 時定数 操作 ゲイン むだ時間 時定数 .SUBCKT PRMF PV CNOT DST PARAMS: KD=1 TD=1 KC=1 TM=1 TC=1
◆ 1 次遅れ + 無駄時間の周波数応答を、図 3-2-15に示します。
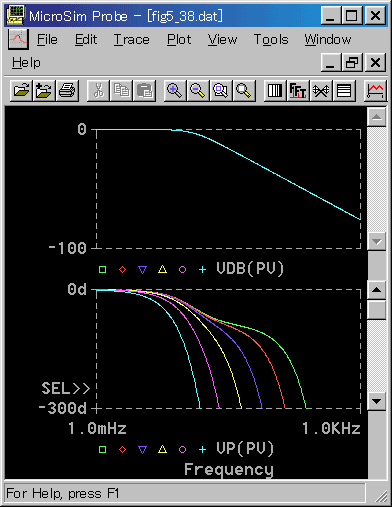
◆ ゲインは 1 次遅れと等しく、位相は 1 次遅れに無駄時間が加わっています。
位相に関しては、L = 0.03 では、低周波部分に 1 次遅れの特性が残っていますが、L が大きくなると、ほとんど無駄時間だけの感じになります。
1 次遅れ + むだ時間のステップ応答は、図 3-2-16のようになります。
[図 3-2-16] 1 次遅れ + むだ時間のステップ応答
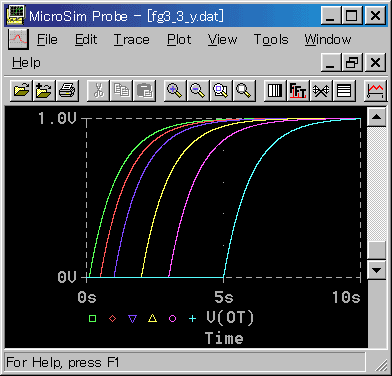
◆ 一般に、2 次以上の遅れでは、立ち上がりの部分に角が無く、滑らかに立ち上がります。これを表現したり、振動的な応答を含めたりするために、2 次遅れ + むだ時間を使用することもあります。
この講座では、1 次遅れ + むだ時間を使用します。
◆ 3.1.3.(1-B-b)で、制御対象の例として、液面系を示しました。液面系は 1 次遅れです。1 次遅れでは、位相が -180°を横切りません。この意味では、不満足なモデルです。
しかし、1 次遅れモデルも、利用価値はあります。
一般に、制御対象の特性は複雑です。通常は、近似モデルを作ることになります。1 次遅れモデルは、液面系の第 1 近似モデルです。必要に応じて、さらに詳細なモデルを付け加えます。
制御対象は、複数の制御要素の集まりと考えられます。液面系は、液面自体の系と、流出量を制御するバルブ系の直列と見なすことができます(図 3-1-18、図 3-2-17)。
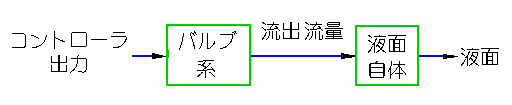
◆ 式 3-1-12 は、第 1 近似として、バルブ系の動特性を無視して、液面自体だけをモデル化したのです。バルブ系を考慮して、これを 2 次遅れで近似すれば、総合して、3 次遅れになります。
第 1 近似で液面系を 1 次遅れと見なすことができたのは、液面自体の周波数応答と、バルブ系の周波数応答とで、その周波数帯域が、大きく異なるからです(図 3-2-18)。
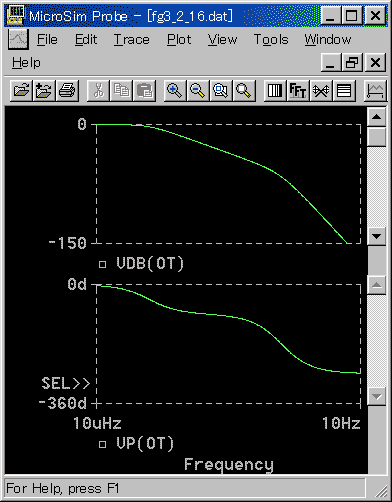
◆ 図で、低周波領域(左 2/3 の範囲)では、かなり広い周波数帯域で、1 次遅れの特性が、はっきり現われています。この部分が 液面だけの第 1 近似の部分です。液面系を 1 次遅れであるとしたのは、このことによります。
このあと、高周波に部分に、3 次遅れの特徴である、ゲインの-60dB / dec、位相の-270°が現われています。これが、バルブの部分の特性です。
この液面系の制御において、即応性の高い、最適な制御系の設計を行うためには、安定限界付近の周波数の周波数応答が必要です。
[注] 液面制御系では、比例ゲイン KP の値を故意に最適値から大幅に小さくして、ゆっくりした応答で使用することも多いのです。このことについては、6.3.2 コラム 6-3-3 で説明します。
◆ これに対して、図 3-2-19 のような周波数特性を持っている制御対象は、当然、1 次遅れで近似することはできません。3 次遅れで近似する必要があります。
[図 3_2_19] 常に 3次遅れで近似しなければならない特性
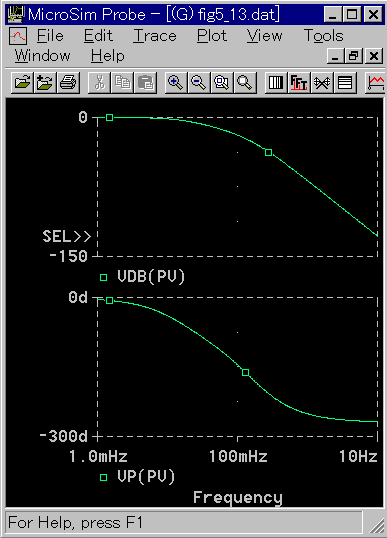
◆ 以上は、制御対象を、それぞれ単体として眺めた場合の検討です。
しかし、制御対象は、一般に複雑なシステムを構成しています。制御対象をシステムとして眺めてみます(図 3-2-20)。
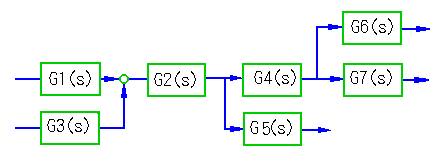
◆ 制御系を組む、すなわちコントローラを取り付けるときは、制御対象システム の中の、ある場所を制御変数として選び、別のある場所を操作変数に選定するわけです。
そのとき、選んだ制御対象モデルは、一般に複数の制御要素から成っています。
それが全体として、一巡伝達関数としての条件(位相が-180°を過ぎる)を満足していれば十分です。制御系を構成する、個々の制御要素が、この条件を満足している必要はありません。
◆ 制御対象モデルは、実際の制御対象を模擬したものです。実際との一致性が問題になります。しかし、一致性は、そのモデルの目的用途によって、異なります。
制御対象モデルには、2つのタイプがあります。
1 つは、ある与えれた、特定の制御対象の特性を実現できれば良い場合です。既に存在する制御対象対象について、シミュレーションによる制御の解析を行いたい場合には、このモデルで、十分です。
既に説明してきた制御対象モデル(3次遅れモデルや、1 次遅れ + むだ時間モデル)は、このタイプに対応するモデルです。このタイプのモデルの形式は、モデルパラメータの値によって、できるだけ広い範囲の制御対象に、適合できる、モデルであることが必要です。
ただし、作成した個々のモデルは、安定限界付近の周波数帯域で、適合すれば十分であり、広い周波数範囲で適合する必要はありません(3.2.2.(5))。
制御対象の特性を実測して、その実測データから、モデルを作る場合には、このタイプのモデルになります。実測データからモデルを作る方法は、次の (5) に示します。
◆ もう 1 つは、制御対象の特性自体を変えて、ケーススタディを行いたい場合です。
このタイプのモデルは、制御対象モデルの構造が、実際の制御対象と、物理的（または化学的)に、ある程度対応していることが必要です。
6.1 章に示す、モータのモデルは、このタイプに属します。
◆ 制御対象の応答を実測して、その実測データから、シミュレーションモデルを作ります。実測する応答は、ステップ応答、パルス応答、周波数応答の、3 種類が考えられます。
ステップ応答は、測定、モデル作り、共に簡単です。ただし、モデルの精度は高くありません。とくに、高周波の情報が得られないという欠点があります。
パルス応答 は、入力にパルス(半正弦波)を使用します(図 3-2-21)。
◆ 測定は、比較的簡単であり、制御対象に与える影響が少ないという特徴があります。しかし、測定データから、モデルを作るデータ処理が面倒です。また、ステップ応答と逆に、低周波の誤差が大きいという欠点があります。
この誤差の問題は、使用する入力信号自体に含まれる、情報に依存しています。すなわち、ステップ入力には高周波成分が少なく、パルス入力には低周波成分が少ないのです。
周波数応答は、入力信号の周波数範囲を広く取れば、その範囲の周波数情報を得ることができます。この点では優れています。しかし専用の測定器を必要とし、測定に時間が掛かります。
◆ この講座では、簡便な、ステップ応答から作る方法を紹介します。
◆ 従来から紹介されているやり方です(図 3-2-22)。
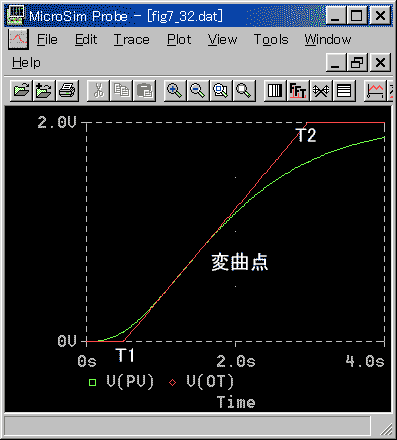
◆ ステップ応答の応答曲線(緑)上の変曲点に接線(赤)を引きます。この接線が、横軸をよぎる点までの時間 T1 が無駄時間です。
また、ステップ応答曲線が平衡に達したときの値と、接線との交点の時間を T2 とすれば、T2 - T1 が 1 次遅れの時定数になります。
PSPICE 上で、この作業を行うことができます。
実測データを入力するには、デバイス 電圧源 V の折れ線近似波形を使用します。書式は、
<V(名称)><+ノード><-ノード>PWL(<t1><v1><t2><v2>・・・<tn><vn>)
( < > は必須 )
です。<ti><vi> が、折れ点の座標です。上記の書式のままでは、分かりにくいので、たとえば、下記のように、区切り記号を入れると、見やすくなります。
VP 1 0 PWL (0,0)(1,1)(2,1)(3,0)
データの入力は、時間間隔を等しくしないで、特に変曲点の付近を詳しく、正確に入力します。
データ入力後の処理は、上記入力の代わりに、制御対象標準 K を使用した例によって、図 3-2-23 に示します。
[図 3-2-23] 標準 K の制御対象を 1 次遅れ + むだ時間で近似する
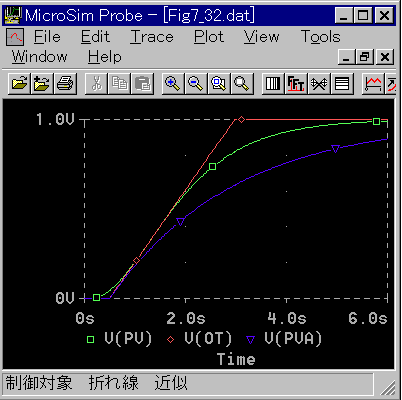
◆ ステップ応答波形から、制御対象の 1 次遅れ定数とむだ時間を求める標準回路ファイル APRX1D.CIR を用意しました。図 3-2-23 もこれを利用しています。この回路ファイルでは、接線を電圧源(パルス波形)で作っています。すなわち、
V<名称> OT 0 PULSE (0, {KC}, {TM}, {TC} )
です。
まず、パラメータ KC の値を、入力ステップ応答が平衡に達したときの入力変数値にします。
その上で、パラメータ TM と TC を調整して、入力ステップ応答曲線(緑)の変曲点で、折れ線(赤)が接するようにします。このときの TM が等価むだ時間、TC が等価時定数です。
◆ 求まったモデルは、変数 PVA で表示できます(青)。図の V(PVA) は、入力ステップ応答曲線と、かなり異なりますが、これで、データを取ってみます。求まった標準 K の等価むだ時間は 0.497s、等価時定数は 2.495s です。
モデルと、元の標準 K の制御対象との比較が、図 3-2-24 (周波数応答)、および図 3-2-25 (制御応答)です。
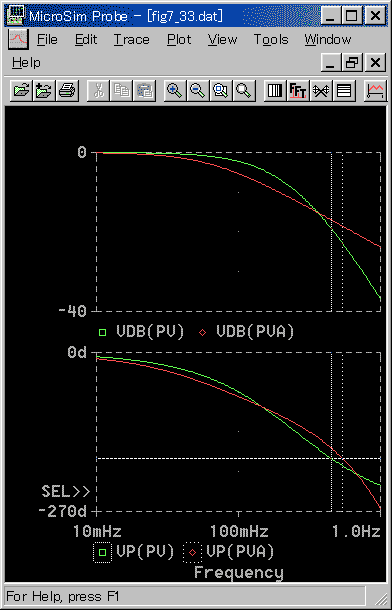
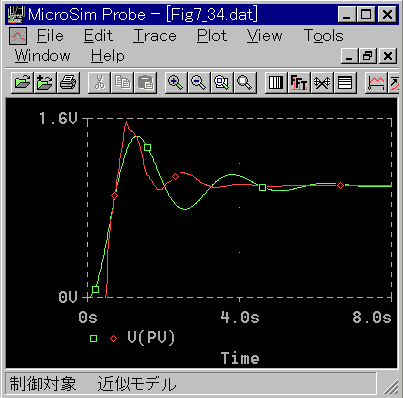
◆ 図 3-2-25 制御応答での、制御パラメータの値は、それぞれのモデルに合わせてあります。
結論として、かなり違いがあります。変曲点に接線を引くというやり方は、以上の実験からは、良好な近似であるとは言えません。手作業を前提とした時代では、簡単さが第 1 でしたから、やむを得ないことと思われます。
制御対象を、標準 N とした場合を、図 3-2-26〜図 3-2-28 に示します。
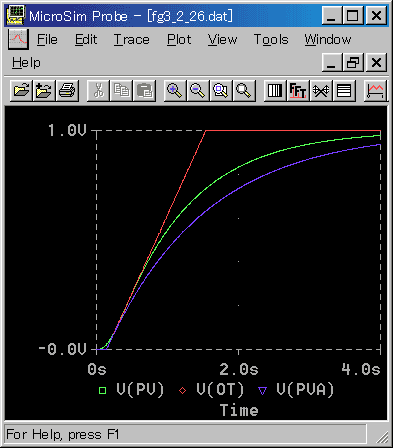
◆ 求まった等価むだ時間は 0.155s、等価時定数は 1.34s です。
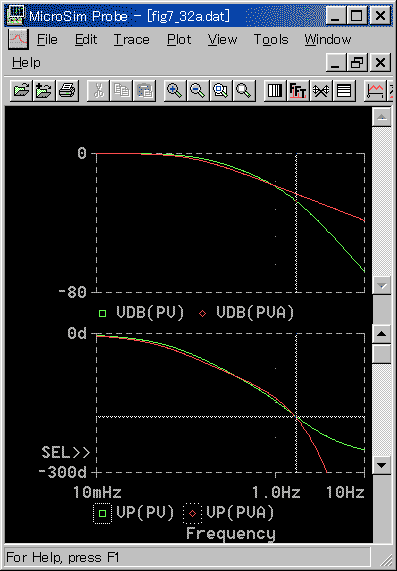
◆ 標準 K と比べれば、かなり良く一致しています。しかし、位相は、安定限界の周波数までは、非常良く一致していますが、そこから先は、急速に離れてしまいます。ゲインは、安定限界の周波数付近では、かなり傾斜が異なっています。総合して、非常に良い意一致とまでは行きません。
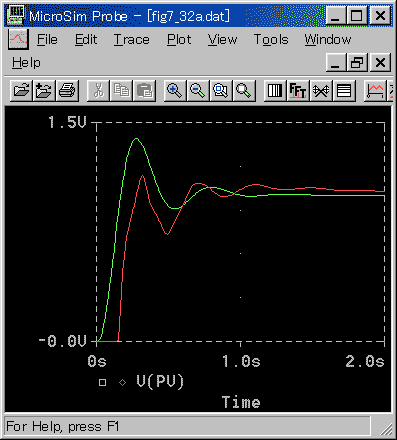
◆ 制御応答も、非常に良い一致とまでは行きません。しかし、標準 K に比べれば、かなり良くなっています。
◆ シミュレータの利用を前提として、近似の方法を改良してみました。
まず、対象曲線の変曲点に接線を引きます。これは従来方式と同じです。
次に、1 次遅れ + むだ時間の近似曲線を、対象曲線の変曲点の位置で、上記接線に接するように決めます。
結果としては、対象曲線の変曲点に、近似曲線を接するように引くわけですが、接線を補助線として入れないと、作業が難しくなります。
この改良方式も、作業用の標準回路ファイル APRX2D.CIR を作ってあります。
◆ 標準 K への適用を図 3-2-29〜図 3-2-31 に、標準 N への適用を図 3-2-32〜図 3-2-34 に示します。
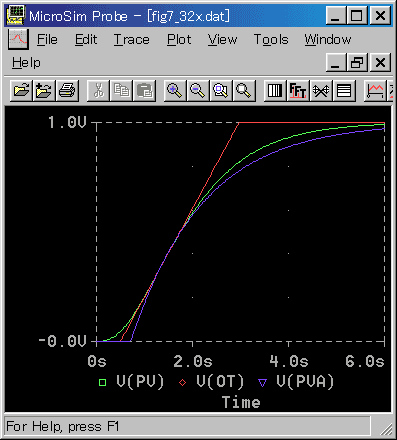
◆ 従来方式と比べると、モデルの近似度は、大幅に改善されています。
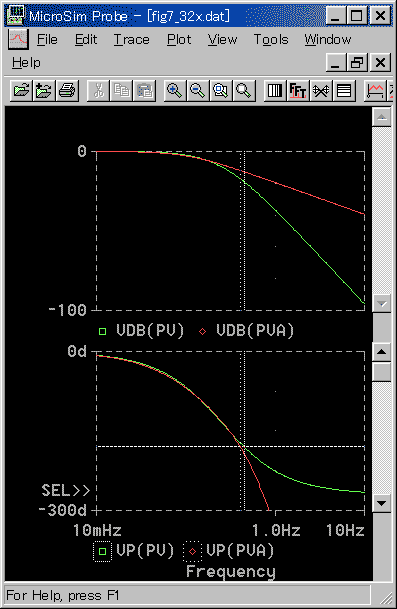
◆ 周波数応答も、従来方式と比べると、かなり良く一致しています。従来方式の標準 N と同程度です。
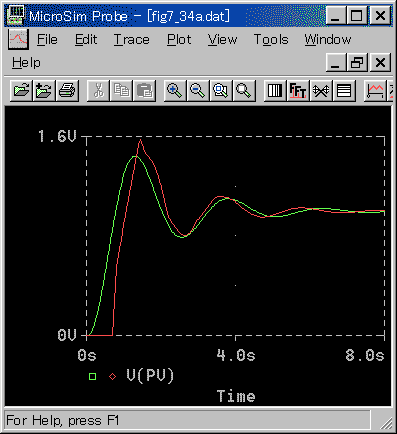
◆ 制御応答は、非常に良く一致しています。従来方式とは格段の差です。ただし制御パラメータの比例ゲイン KP の値は異なります。これは、周波数応答のゲインが異なることに起因しています。
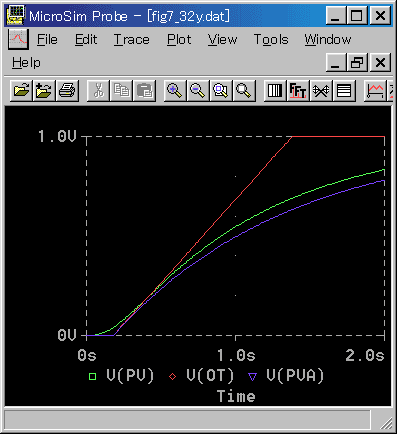
◆ 従来方式でも、かなり良かったですが、さらに良くなっています。
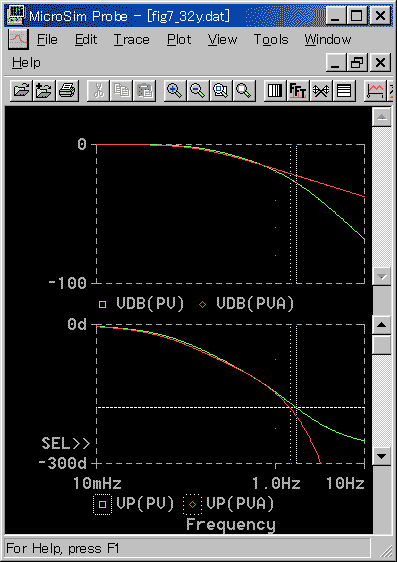
◆ これも、従来方式に比べて若干よくなっています。
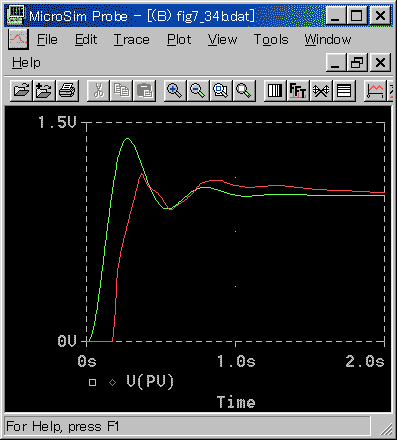
◆ 従来方式よりも、さらに良くなっています。
以上を総合して、改良方式は、従来方式に比べて勝っています。実験したのが、標準 N と、標準 K だけですから、広い範囲にわたって、どの程度適用できるかは、分かりません。しかし、従来方式と比べて、優れていることは、確かと思います。
