◆ 前章は、アナログ制御に関する基礎的な事項、すなわち伝達関数や周波数応答について解説し、基本的な制御要素の性質について説明しました。
この章では、前章の基礎的な技術をベースにして、最も基本的な制御方式であるアナログ PID 制御の特性と、その評価について解説します。
◆ 制御成績を評価するに当たっては、まず最適な応答とは何か? ということが問題になります。最適な応答は制御対象によってそれぞれ異なります。
制御成績を評価するパラメータ は、 1.7.(2) 図 1-38 に示したように、「行き過ぎ量」、「行き過ぎ時間」、「整定時間」、「オフセット」といくつかあります。
また「整定時間」は、制御対象の要求によって決まる「許容誤差」に依存します。
これらの、どれを重要視しなければならないかは、制御対象によって異なり、一定しません。
しかも、これらのパラメータ間には、あちらを立てればこちらが立たないという、相反するものもあります。
したがって、制御対象ごとに、具体的な評価基準を決めなければなりません。
そして、それらの評価パラメータが、その制御対象が要求する範囲に収まれば良いわけです。
その制御系がすでに要求基準を満たしているなら、さらに良い制御成績を求める必要はありません (図 3-2-1)。
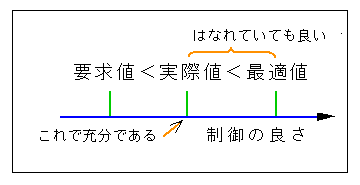
◆ 逆にその制御系において、調整手法を駆使して最適条件が得られたとしても、それが要求基準を満たしていないなら、それで満足するわけにはいきません。
何らかの手段を講じて、要求基準を達成しなければなりません。PID 制御よりも高度な制御演算を検討したり、またさらに、1 段高い立場から、制御システム自体を、再検討することになります。
ただし、これらに関しては、この講座の範囲外です。
[注] ディジタル制御では、単純な PID 制御を、モディファイすることが容易です。高度な制御演算は、この講座の範囲外ですが、簡単なモディファイについては、第 5 章、第 6.3 章で、紹介しています。そこに紹介する程度のモディファイでも、かなりの効果が期待できます。
◆ 制御成績の評価基準は、本来は、それぞれの制御対象によって異なります。
しかし、そうはいっても、制御成績を評価する汎用的・適切な目安が、何かあった方が便利です。評価基準として、次に示す「2 乗誤差面積」が、一般に広く用いられています。
ただし、くどいようですが、あくまでも 1 つの目安です。真に汎用の基準は、あり得ません。この講座でも、以降、説明の目安として、2 乗誤差面積を使用しています。しかし、この点に留意してください。
◆ 2 乗誤差面積 を、式 3-2-1 に示します。
・・・・ (3-2-1)
Ie は評価関数 、e は偏差です。この評価関数は、制御以外の分野でも、広く一般に使用されています。
この式は時間を無限大まで積分していますから、オフセットがあると解が無限大となり評価できません。
しかし、制御演算式に積分動作 (I動作) が入っていれば、オフセットはゼロになります。
通常は積分動作を使用することが多いので、この評価関数は、一般性があります。
オフセットがある場合は、式 3-2-1 をモディファイして、
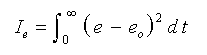・・・・ (3-2-2)
を使用します。ここで、eo はオフセットの大きさです。
◆ この評価関数を、そのまま適用すると、最適な制御応答では行き過ぎ が発生し、振動的な波形になります ( 1.7.(4-B) 図 1-39 の「行き過ぎ有(黄色)」の波形)。
PSPICEでは、PROBE 画面に、2 乗面積誤差を表示させることができます(コラム 3-2-1参照)。これを利用して、制御変数の波形と、2 乗誤差面積との関係を、見てみましょう(図 3-2-2、図 3-2-3)。
[図 3-2-2] 行き過ぎを許容する場合の 2 乗誤差面積
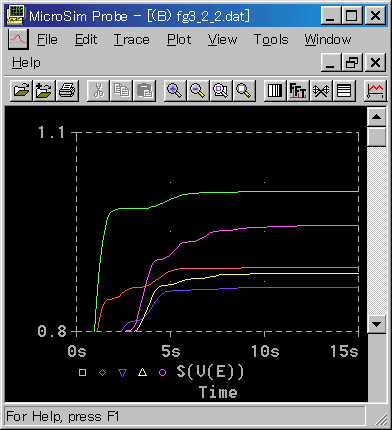
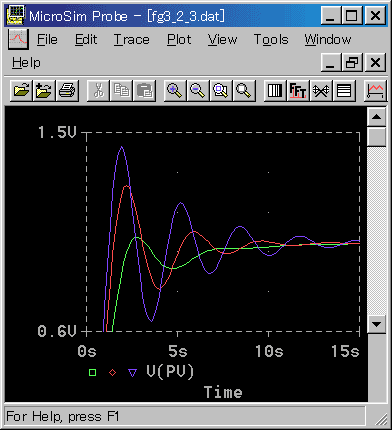
◆ 行き過ぎが小さいときは、立ち上がりが遅く、立ち上がりの部分で誤差面積が大きくなっています。
行き過ぎが大きいところでは、立ち上がりが早く、立ち上がりの部分の誤差面積は小さくなっています。しかし振動が激しいと、振動の部分の誤差面積が大きくなります。
したがって、その中間に誤差面積最小、すなわち最適な応答が存在します。その最適応答が、KP = 2.5 であり、1.7.(4-B) 図 1.39 の「行き過有」です。
◆ 制御対象によっては、行き過ぎを、許容できない場合があります。この場合には、行き過ぎを許容しないという条件の下で、式 3-2-1を最小にする応答を使用します (図1-39 「行き過ぎ無(青色」)。
一見したところでは、行き過ぎ無し 方が全ての面で優れているように見えます。しかし、この行き過ぎ無の応答波形は、立ち上がりが、行き過ぎ許容よりも、遅くなっています。
この立ち上がりの部分の 2乗誤差面積が大きいので、評価関数の値は、行き過ぎを許容する場合よりも、大きいのです。
図1.39 に、2 乗面積誤差を付け加えたものが、図 3-2-4 です。
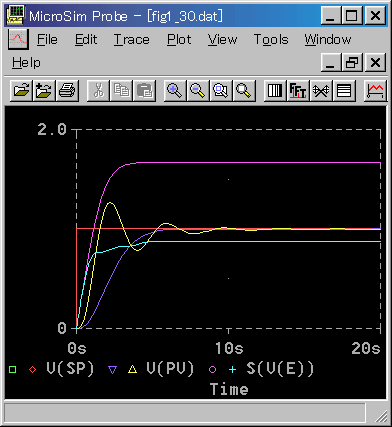
◆ 行き過ぎを許容しないものが、許容するものに比べて、2 乗誤差面積が大幅に大きいことが分かります。そして、その原因が、最初の立ち上がりの部分あることも分かります。
この、2 乗誤差面積は、同じ評価関数で、条件無しと、行き過ぎを許容しないという条件付と、２ つのケースに対応できます。この点が便利なところであり、2 乗誤差面積法の汎用性を高めています。
実際の制御においては、両者の中間の応答が、最適と考えられる場合も多いでしょう。
たとえば、完全な行き過ぎ無しでは、即応性が低下します。若干の行き過ぎを許容すれば、応答を速くすることができます。
[コラム 3-2-1] PROBE 画面に 2 乗誤差面積を表示する
★ PSPICE では、PROBE 画面に、2 乗誤差面積の値を表示させることができます。
PROBE は、式を使用できます。加減乗除の他に、「表 2-2-2 SPISE で使用できる関数」を使用できます。さらに下記の、PROBE でのみ使用できる関数があります(表 3.2.1c)。
| SGN(x) | (x >0 なら) +1、(x=0 なら) 0、(x<0 なら) -1 |
| M(x) | x の振幅 |
| P(x) | x の位相 |
| R(x) | x の実数部 |
| IMG(x) | x の虚数部 |
| DB(x) | 20×log(|x|) (対数の底は 10) |
| d(x) | X 軸変数についての x の微分値 |
| s(x) | X 軸変数についての x の積分値 |
| AVG(x) | X 軸変数についての x の平均値 |
| RMS(x) | X 軸変数についての x の実効値 |
| MIN(x) | x の実数部の最小値 |
| MAX(x) | x の実数部の最大値 |
★ 表 3-2-1c 中の、s(x) は積分ですから、これを 2 乗誤差面積に使用します。偏差を V(E) とすれば、
S ( V(E) * V(E) )
が、2 乗誤差面積になります。これを PROBE 画面に表示させます(2.1.4.(3))。このとき、Add Trace ダイアログボックス下部の、Trece Expression 欄に、式を記入します。
★ なお、式が複雑だと、入力に手間が掛かります。S(x) に記入する式は、回路ファイルに使用できる関数を使用している場合が多いと思います。
この場合、元の回路ファイルで予め式を立てておいて、その電圧(たとえば V(E))を使用すれば、この欄の記入は、S(V(E))のように簡単になります。
★ 十分時間が経ったところでは、2 乗誤差面積の値が一定になりますから、この一定になった値を読み取ります。
★ なお、この一定になる前の途中の経過も、有効な情報として利用できます。
◆ 以上の検討は、目標値変化に対する、ステップ応答について、行ってきました。フィードバック制御では、外乱入力 に対する評価も必要です。2 乗誤差面積を使用して、外乱入力のステップ応答について、検討します。
先ず、目標値変化のときと同様に、応答波形と 2 乗誤差面積との対応を求めます(図 3-2-5、図 3-2-6)。
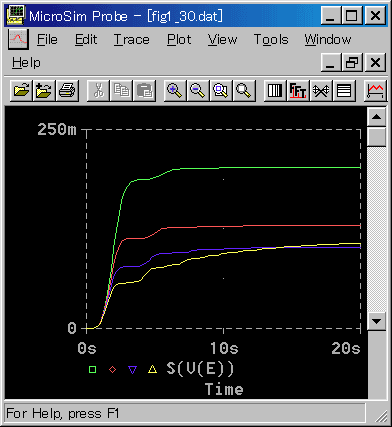
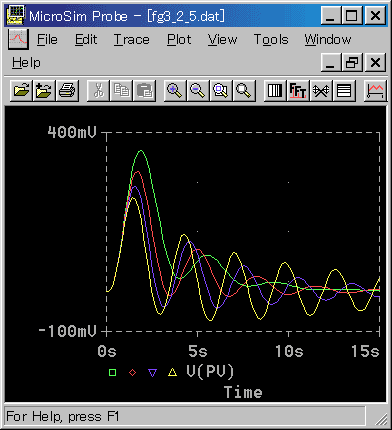
◆ 目標値入力に比べて,大きな違いがあります。比例ゲイン KP の値が最も小さいのが、目標値入力で最適であった KP = 2.5 です。
2 乗誤差面積は、比例ゲイン KP が、2.5 よりも、ずっと、大きいところ KP = 4.5 で、最小になっています。たたし、その条件では振動がかなり継続しています。したがって、2 乗誤差面積最小が、最適とは見なせない可能性が高くなります。
なお、KP = 2.5 の条件は、振動的ではありますが、行き過ぎには、なっていません。
いずれにしても、振動が激しい解を避けるなら、2 乗誤差面積最小からは、外れたところが選ばれることに、なるでしょう。
[注] 一般に、定性的には似た傾向がありますが、制御対象特性の違いによって、定量的には、かなり異なります。
◆ 実際の制御においては、外乱だけ発生して、目標値は永久不変というケースは、あまり無いでしょう。したがって、目標値を変化させたときに、行き過ぎが大きく、振動過多であっては、使い物になりません。
結局、両者を勘案して、総合評価することになります。目標値変化と外乱入力の、どちらを重視するかで、最適解が異なります。
[注]
ディジタル制御を使用する場合は、PID 制御をモディファイすることによって、目標値変化、外乱入力の両方に対して、ある程度適切な制御を行わせることが可能です(5.3.(2)参照)。
また、さらに高度な制御を行えば、両方に対して、それぞれ最適な応答が得られます。ディジタル制御は、アナログ制御と異なり、制御演算式を、モディファイすることが容易です。
