◆ この章から、ディジタル制御です。ディジタル制御の解説のやり方は、いろいろあります。最近では、アナログ制御抜きに、はじめからディジタルシステムとして論じるやり方が、多くなっています。
この講座では、最初に、アナログ制御について説明しましましたから、アナログ制御をベースとして、アナログ制御と比較しながら話を進めます。
ディジタル制御においても、シミュレーションを活用することができます。
この講座では、ディジタル制御にも、PSPICE によるアナログ回路シミュレータを使用しています。ディジタル制御のシミュレーションに、アナログ回路シミュレーを使用することができます。このため、効率は悪いのですが、アナログ制御との比較が容易です。
◆ ディジタル制御では、変数の値はディジタル化された、飛び飛びの量子化された値になります。時間軸もサンプリングによって、非連続になります(1.5.(4-C)図1.23、24)。
このためアナログ情報の一部が失われます(図 4-1-1)。
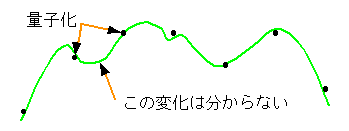
◆ すなわち、変化している途中の値は、量子化によって分からなくなります。コントローラは、入力した情報(変数の値)を唯一の手がかりとして、制御を行ないます。
ディジタル化によって、入力する情報量が元のアナログよりも減るのですから、制御演算式が同じなら、当然ディジタル制御の方が、制御成績は悪くなります(1.5.(5))。
◆ 1.5.(2)に述べたように、デイジタル制御の制御成績が良くなるのは、アナログ制御よりも高度な制御演算を行なうからです。
ディジタル制御の制御演算はソフトウエアです。制御演算式を高度化しても、あまりコストアップ要因にはなりません。
これに対してアナログ制御では、技術的には可能であっても、著しいコストアップになるために、高度な制御は少なく、ほとんど PID 制御に限定されます。
高度の制御演算式は、うまく使えば良い制御成績が得られます。しかし使いこなすためには、それなりの技術が必要です。
PID 制御は使い易いことが特徴です(表 4-1-1)。PID 制御で充分な制御成績が得られるならば、あえて高度な制御演算式を使う理由はありません。
| - | コスト | 制御成績 | 使いやすさ |
| PID制御 | ○ | △ | ○ |
| 高度な制御 | ○ | ○ | △ |
◆ この理由から、デイジタル制御においても、PID 制御が多く使われています。また高度な制御を行なう場合でも、PID 制御とは全く別な制御演算式を使わないで、PID 制御をベースとした制御が多く使用されています。
◆ ディジタル制御は、変数軸、時間軸ともに量子化 され、飛び飛びの値になります。これは、制御成績が悪くなる要因として働きます。
このとき、変数軸と時間軸とでは、制御成績への影響のしかたが異なります(表 4-1-2)。
| - | オフセット誤差 | 動的応答の劣化 |
| 変数軸の量子化 | 有 | 少 |
| 時間軸の量子化 | 無 | 有 |
◆ 一般に、オフセット誤差に対する要求は厳しいことが多いので、変数軸の量子化は、十分に細かくします。すなわちA/D(アナログ／ディジタル)変換の桁数を、十分に大きく取ります。
◆ 時間軸の量子化は、オフセット誤差の要因にはなりません。したがって、制御対象によっては、サンプリング周期を長く取ることができます。
制御演算式が複雑であると、制御演算式の実行時間が長くなります。その他、A/D 変換速度など、サンプリング周期を短くできない、ないしはコストアップになる要因があります。
したがって、サンプリング周期が制御成績に与える影響を評価しなければならないことがあります。ディジタル制御の理論は、このような要求から生まれました。
ディジタル制御の理論においては、変数軸は、量子化が十分に細かいことを前提として、量子化したことを無視し、アナログとして取り扱います。
そして、サンプリング を行なっていることに関して理論を展開します。
サンプリングをともなう制御のことを、サンプル値制御 といいます。ディジタル制御の理論は、名前は、ディジタル制御ですが、実体、はサンプル値制御の理論です。
◆ ディジタル制御系のハードウエア構成は、1.5.(4-A) 図 1.20、図 1.21 に示しました。これを信号の流れとして見ると、図 4-1-2のようになります。
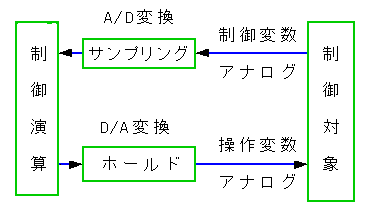
◆ 制御対象から出力される制御変数はアナログです。これを A/D 変換器でディジタルに変換します。しかしディジタル化したことは無視し、サンプリングと見なします。
コントローラ内の制御演算は、ディジタルです。しかしコンピュータの演算ですから、量子化は十分に細かく、この意味ではアナログと同等と見なすことができます。
制御演算の結果は D/A 変換されます。これもディジタルをアナログに変換していることを無視して、ホールドと考えます。時間的に飛び飛びの値を相互につないで、時間的に連続な値に変換することを、ホールド といいます(図 4-1-3)。
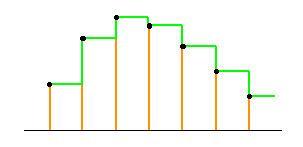
◆ A/D 変換器は、原理的にサンプリングの機能を含んでいます。これと同様に、D/A 変換器も本質的にホールドの機能を内蔵しています。
◆ ディジタル制御においても PID 制御が多く使用されています。PID 制御を例にとって、ディジタル制御の演算式を説明します。PID 制御以外でも、考え方は同じです。
アナログ PID 制御の基本式(時間領域)は、式 1-2 に示しました。まずこの式をディジタル化して見ましょう。ディジタルの変数を図 4-1-4 のよう表わします。
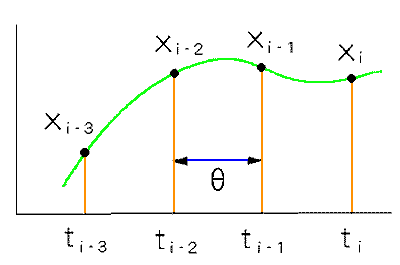
◆ サフィックス i が、現在のサンプリング時点を意味します。サフィックス i-k は、現時点から k 回前のサンプリングです。
式 1-2 の第 1 項は、ディジタル化によって、単にサンプリングになるだけです。 第 2 項は積分です。アナログの積分は、
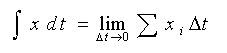・・・・ (4-1-1)
で定義されます。アナログは連続ですから、Δt → 0 とすることができます。ディジタルは、サンプリングですから、最小値はサンプリング周期 θ です。したがって Δt → 0 の代わりに Δt → θ と置けば、それがディジタルにおける積分 です。
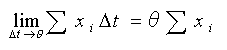・・・・ (4-1-2)
ただし後に述べる理由によって、この式を変形した
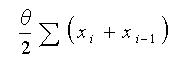・・・・ (4-1-3)
の方が、よりアナログの積分に近いので、この講座では、式 4-1-3 を使用することにします。この式は、Xi を足し込む代わりに、前回との平均値を足し込んでいます。この式は、最新の足し込みが、1/2 になりますが、xi-1およびそれ以前の値は、Σxi と同じですから、実質的に、Σxi と同じです。
ディジタルにおける微分 も、積分と同様に考えて、
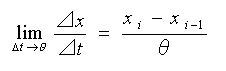・・・・ (4-1-4)
となります。
◆ 以上を総合すると、ディジタル PID 制御の演算式は、
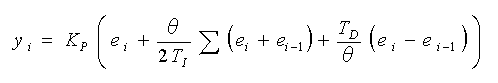・・・・ (4-1-5)
で表わされます。
制御演算式には、サンプリング周期 θ が入っています。時間軸をサンプリング周期 θ でノーマライズすると、
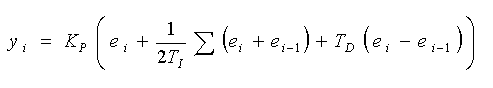・・・・ (4-1-6)
になります。一般には、このノーマライズした式(または積分項を式 4-1-2 にしたもの)が多く使われています。しかしこの式 (4-1-6) は、時間軸をサンプリング周期で、ノーマライズしていることを、忘れてはいけません。
この講座では、サンプリング周期のことを忘れないように、実時間の式 (4-1-5) を使用します。
◆ アナログ制御では、D 動作(微分動作)を含むときは、フィルタを入れた式でないと、実用になりませんでした。また時間領域で干渉が無い時間領域形と、周波数領域で干渉がない周波数領域形、などがありました。
ディジタル制御でも、これらのアナログ式に対応する演算式が存在し、利用されています。しかし、これらについては、もう少し話が進んでから解説します。
