


◆ ホールドは、むだ時間に近い特性を持っており、むだ時間で近似することも可能です(4.1.4.(3-C-b))。また出力処理における、出力の遅れは、むだ時間そのものです(4.1.2.(4-A))。
したがって、ディジタルコントローラは、図 4-2-32 のように考えることができそうです。

◆ ディジタル制御は、パルス伝達関数で表されます。パルス伝達関数は、Z 変換領域の関数ですが、これをラプラス変換領域に換算することによって、PSPICEによるシミュレーションが可能です。
この講座では、これを利用して、ディジタル制御の解説を行ってきました。しかし、パルス伝達関数の計算は、アナログの伝達関数の計算に比べて、とくにトランジェント解析は、かなり、演算時間が掛かります。
最近のパソコンの演算能力は高いので、それほど苦にはなりませんが、それでも、軽快というわけには行きません。また、従来の低速のパソコンを利用する場合もあるでしょう。
図の、アナログモデルが有効に利用できるなら、ディジタル制御の演算は、格段に速くなります。
という訳で、アナログモデルを検討してみました。
◆ アナログモデル は、アナログ制御のサブサーキットと、等価むだ時間のサブサーキット DAHE とを、組み合わせて作ります。
アナログ制御のサブサーキットは、PIDA (周波数領域形)、PIDJ (時間領域形)など、任意のものを選択できます。
等価むだ時間のサブサーキット DAHE は、ホールドをむだ時間で近似したものと、出力処理の遅れとを、組み合わせたものです(リスト 4-2-3 )。
[リスト 4-2-3] ディレイアンドホールド(.TRAN 用)
*** ディレイアンドホールド( 等価むだ時間モデル ) $ DAHE
* 操作出力 入力 サンプル周期 ディレイ(0〜1)
.SUBCKT DAHE CNOT IN PARAMS: TS=1 TL=1
E1 CNOT 0 LAPLACE {V(IN)} = {EXP(-(0.5+TL)*TS*S)}
.ENDS
|
◆ 図 4-2-32 のように考えたアナログモデルと、まともなディジタル制御とを、周波数応答で、比較して見ます。先ず、PI 動作を、図 4-2-33 に示します。
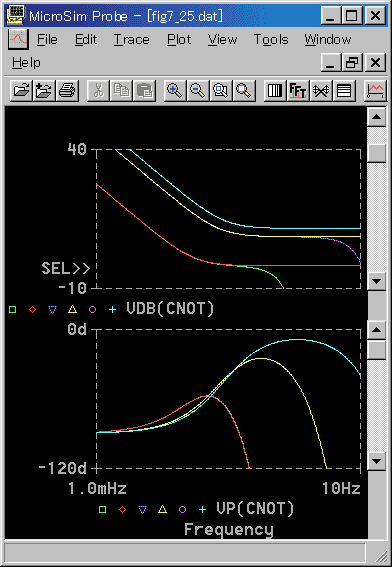
ディジタルとアナログは、実用範囲で、ほぼ、完全に一致しています。
◆ PID 動作は、実用式を図 4-2-34 に、基本式を図 4-2-35 に示します。
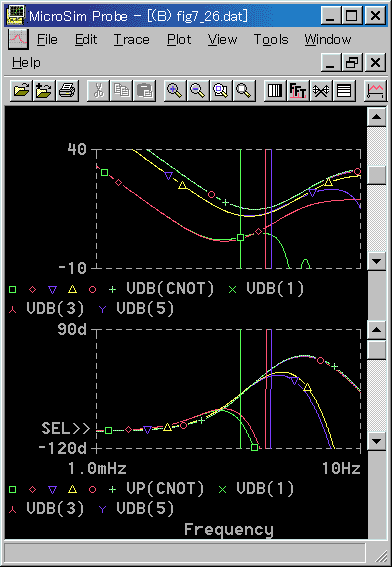
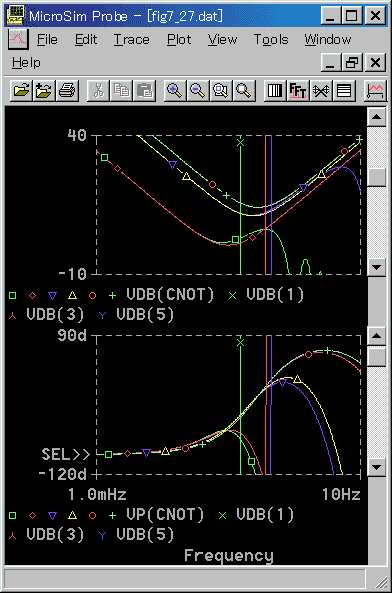
◆ 図には、アナログモデルについて、限界感度法で求めた、各々の限界周波数を入れてあります。これも、まともなディジタル制御と、実用範囲で、かなり良く一致しています。
◆ アナログモデルを使用した制御応答を図 4-2-36〜図 4-2-40に示します。比較のために、まともなディジタル制御も入れてあります。
なお、実験条件は、限界感度法のとき(4.2.4.(2-B))と同じです。
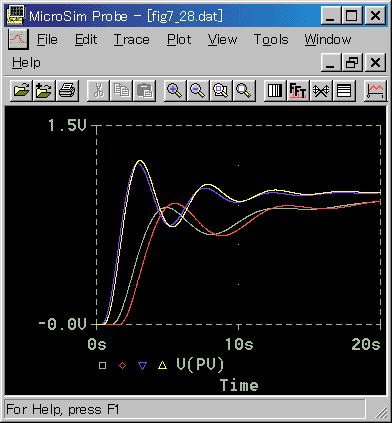
◆ TS = 1 では、若干の差がありますが、広い範囲で、良く一致しています。
[注] 図に示してない、さらに短いサンプリング周期では、もちろん十分に一致しています。
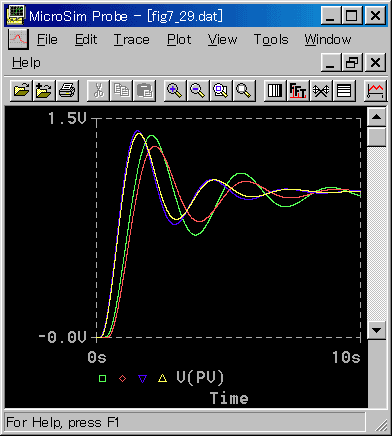
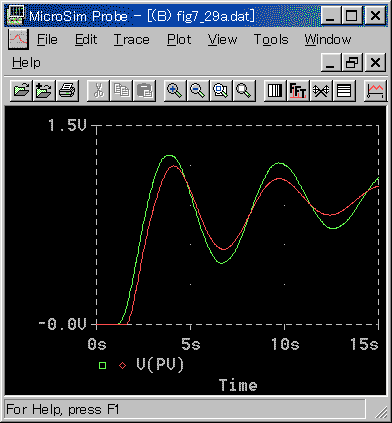
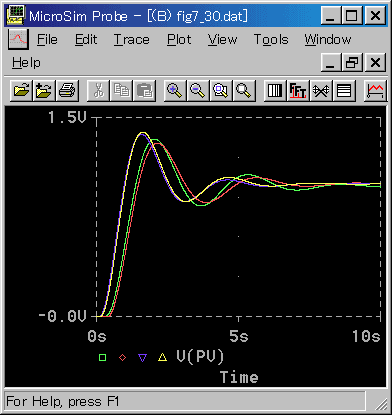
[図 4_2_40] 制御応答(PID 動作(基本式)(その2)
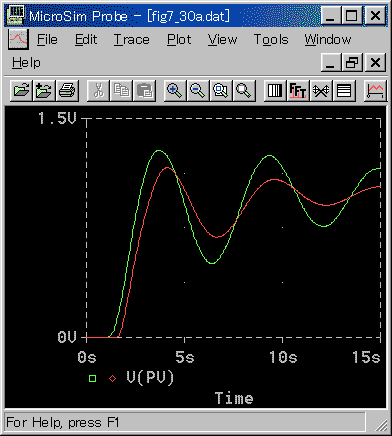
◆ PID 動作では、実用式と基本式との差は、ほとんどありません。PI 動作と比べると、範囲、一致度ともに劣ります。
TS = 72m (TD / TS = 5)以上では、十分一致しています。TD / TS がそれ以下では、正確な応答をチェックするのは、難しいと思いますが、一応は使用に耐えると考えられます。大体の目安を付けるには十分です。