


◆ 周波数応答では、フィードバック制御のループを開いたときの特性から、ループを閉じた制御時の特性を推定することができます。
制御ループを開いたときの伝達関数のことを、「一巡伝達関 数」といいます (図 3-2-7)。
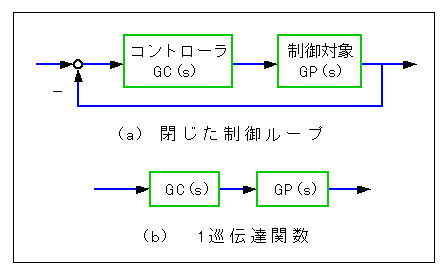
◆ ループは、どこで開いても、一巡伝達関数自体は変化しませんが、図のように開くか、または操作変数のところで開くのが、分かりやすいでしょう。
ループを閉じ、制御している状態で制御系の解析、設計を行うのと比較して、この一巡伝達関数を使用することの利益は何でしょうか?
シミュレーションによって制御系の解析、設計を進める場合には、ループを開いたときも、閉じたときも、その応答波形を求める手間は同じです。
しかし伝達関数を手計算するときは、ループになったものを計算するのに比べて、直列系を計算することは、かなり簡単です。制御の問題を、手計算で行っていた時代には、極めて有効な手法でした。
◆ また多くの場合、制御対象の伝達関数は、制御要素の直列接続の形になります。直列形の周波数応答は、大略の周波数応答波形を、個々の制御要素の周波数応答から比較的容易に推定することができます(コラム 3-2-2 参照)。
しかし、ループ形の伝達関数では、個々の制御要素の周波数応答が分かっていても、ループを閉じたときの周波数応答は、簡単に推定することはできません。
この推定の容易さは、シミュレーションで、解析、設計を行っているときにも、非常に有効です。
シミュレーションを行うこと自体は、ループを閉じていても、開いていても、ほとんど違いはありませんが、解析を進めるときの、見通しの良さが大きく異なります。
まず、ループを開いた状態で解析を行い、ある程度の見通しを立ててからループを閉じて解析する、という手順が考えられます。
★ ボード線図によって周波数応答を表わすと、直列接続の伝達関数の周波数応答を、個々の伝達関数の周波数応答から、容易に作図で求めることができます。
比較的単純な波形であれば、作図無しに、目視でも見当を付けることができます。

★ 二つの伝達関数 G1(X)、G2(X) およびその直列合成 G(X) の関係は、図に示すとおりですから、その周波数応答も
G(jω) = G1(jω)・G2(jω)
となります。これは、二つの複素数の積です。複素数をベクトル形 (γ,φ) (3.1.2.(3-C) 図3-1-15 参照) で表現すると、二つの複素数は (γ1,φ1)
および (γ2,φ2) です。
★ 二つの複素数の積 (γ,φ) は、
(γ,φ) = ( (γ1・γ2) , (φ1 + φ2) )
という関係があります。すなわち、直列合成の振幅は両者の振幅の積、直列合成の位相は両者の位相の和となります。
★ ところで、ボード線図上では振幅は対数表示です、したがって、
log(γ1) + log(γ2) = log(γ1・γ2)
となり、振幅はボード線図の上では加算になります。また、位相はもともと加算です。
★ すなわち、ボード線図の上では振幅、位相ともに加算で作図することができます。次の図は、シミュレーション波形ですが、作図することを想定して眺めてください。
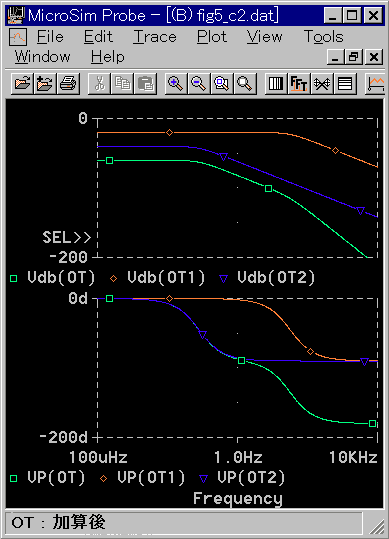
★ 図は、上記のブロック図を表しています。OT1(赤)がG1(X)単体の周波数応答、OT2(水色)がG2(X)単体の周波数応答です(どちらも 1 次遅れです)。
OT(緑)は、それらを直列合成したG1(X)・G2(X)です(1 次遅れ 2 個の直列合成ですから 2 次遅れになっています)。
[注] 図では、G1(X)、G2(X)のゲイン、位相は共に、マイナスの値です。したがって、マイナスの値の加算です。
★ 実際に作図する場合、この例では、元の波形は 1 次遅れです。1 次遅れは、カットオフ周波数のところで曲がる、2 つの折れ線で近似すると簡単です。
もっと複雑な波形でも、幾つかの折れ線で近似できます。そうすれば、図上の加算は、極めて容易です。
★ 正確に作図する場合でも、先ず折れ線近似で作図して、それに肉付けすると良いでしょう。
★ シミュレーションの場合には、作図の手間はありませんが、途中の状態が良く分かるように、PROBE 画面を表示させると、見通しが良くなります。たとえば、

において、最終の D だけでなく、途中の A、B、C も表示させれば、途中の状態が分かります。
★ 必要に応じて、それぞれの要素の周波数応答を表示させれば、さらに見通しが良くなります。
たとえば、「VDB(C)-VDB(B)」を指定すれば、G3(jω) が表示されます(VDB(x)の意味は2.1.6.(2-B-c)参照)。
◆ 一巡伝達関数を使用すると、制御ループを閉じたときの振動の条件を、容易に求めることができます。簡単のために、コントローラは P 動作として説明を進めます (図 3-2-8)。
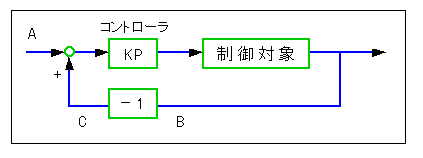
◆ ここで、比例ゲイン KP の値を変えると、一巡伝達関数のボード線図上では、ゲインは上下に平行移動します。位相は変化しません(図 3-2-9)。
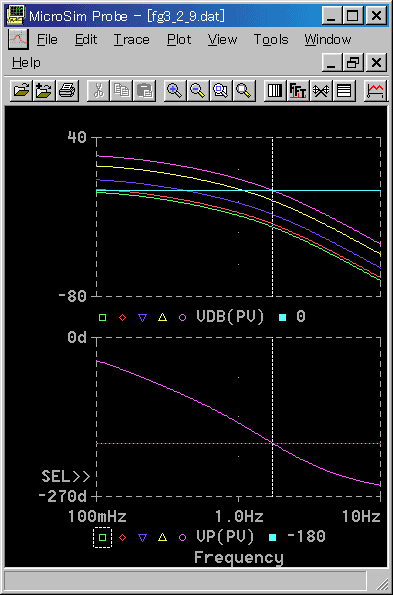
[注] 比例ゲイン KP = 1 のときは、制御対象自体の周波数応答です。
◆ いま、比例ゲイン KP を変化させて、位相が -180°の周波数のところでゲインが、ちょうど 0 dB になるように調整します(図 3-2-9 では KP = 24 です)。
この状態でループを閉じて、最初の入力として、図 3-2-10 の黒線の半正弦波を、図 3-2-8の A に加えます。
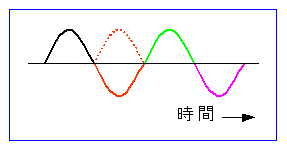
◆ この信号はループを一巡してきます (図 3-2-8 の B、図 3-2-10 の橙色点線)。このとき、振幅は最初の入力に等しく、位相は180°ずれています。
この信号がマイナスされて (図 3-2-8 の C、図 3-2-10 の橙色実線) となり、再びループに入力されます。そして、以下これを繰り返します(図 3-2-10 の緑色、藤色、・・・。
以上のことから、最初に 1 回だけ半正弦波を入力すると、持続振動 が発生することが分かります。
この例では、分かりやすいように、半正弦波を入力しています。実際には、半正弦波に限らないで、何かきっかけになるもの (たとえばノイズ) がループ中のどこかに入れば、以後は、自動的に持続振動になります。
すなわち、この条件は、持続振動が自動的に発生する条件を示しています。
◆ 上記において、もし、位相が -180°ずれて戻ってきたときのゲインが、0 dB より小さければ振動が減衰し、ゲインが 0 dB より大きければ振動の振幅が増大して不安定になるであろうことも、容易に推定できると思います。
ちょうど持続振動する条件は、振動が減衰する安定な状態と、振動が増大する不安定な状態の境になっています。これを「安定限界 」といいます。
安定限界の条件から、安定側に大きく移動するほど、振動の減衰率が大きくなり、安定の程度が強くなります。
逆に安定限界から、不安定な方向に大きく移動するほど、振動の増大率が増して不安定の程度が高くなります。
安定の程度すなわち「安定度 」は振動の減衰率で表わすことができます。この安定度は安定限界からの距離に依存します。
◆ 1.6.(2-A) 図 1-28 などで見てきたように、振動の減衰率が大きいと制御応答は遅くなります。逆に制御応答を速くすると、より振動的になります。
このことから、行き過ぎを許容し、振動的な解になる場合の最適な応答は、ちょうど適度な減衰率の振動をするところにあると、考えられます。
以上のことから、最適な制御応答と、安定限界からの距離には関係がありそうです。
このことを利用して、一巡伝達関数のボード線図から、最適な応答を求めることができます。
この目安になる値として「ゲイン余裕 」と「位相余裕 」が定義されています (図 3-2-11)。
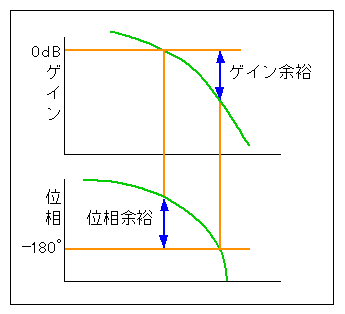
◆ ゲイン余裕 (MG) は、位相が -180°になる周波数におけるゲインの値を (G)dB とすれば、(-G)dB で与えられます。
位相余裕 (MP )は、ゲインが 0dB になる周波数における位相を (P)°とするとき、(180 + P)°です。
このゲイン余裕と位相余裕の値を適切に選ぶことによって、最適な応答を得ることができます。最適として示されている 1 例を表 3-2-1 に示します。
| - | 位相余裕 | ゲイン余裕 |
| プロセス制御 (定値制御) | 16〜80° | 3〜9 dB |
| プロセス制御 (追値制御) | 50°以上 | 4〜9 dB |
| サーボ (機械制御) | 40〜65° | 12〜20 dB |
◆ 表を見て分かるように、かなり大まかなものです。この表から、直ちに最適解が求まるというものではありません。しかし、一応の目安を与えるものです。
制御系の解析、設計を行う場合に、トライアルの出発点を見出すのには、役立ちます。
◆ 次に、ループを閉じて、P 動作の制御を行います(図 3-2-12)。
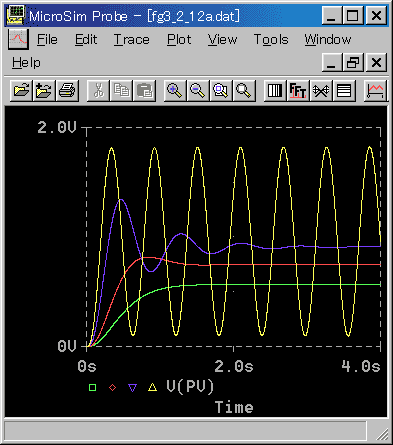
◆ P 動作の制御は、既に1.6.(2-A)に示しました。当然それと同様です。
安定限界である、KP = 24 では、持続振動になります。比例ゲイン KP が、小さくなるにつれて、振動の減衰率が小さくなります。それと共に、振動周波数は低くなり、オフセットは大きくなります。
KP = 10 は、行き過ぎを許容するときの最適条件です。KP = 1.3 は、行き過ぎを許容しないときの最適条件です。このときの、ゲイン余裕等を、表 3-2-2 に示します。
[注] 図 3-2-9 から求めることができます。
[表 3-2-2] 最適条件におけるゲイン余裕等

周波数は、位相余裕における周波数です。
◆ この表から、制御系の解析、設計に必要な、周波数応答の、周波数帯域を求めることができます。
安定限界の周波数(この例では、1.74Hz) より高い周波数は、発散条件ですから、これ以上の周波数は不要です。
行き過ぎを許容する最適条件、およびその近辺の周波数帯域(この例では、1.74〜1.08〜Hz の近辺)が、最も必要と考えられます。
制御対象によっては、行き過ぎを許容しない最適条件の付近(この例では、1.08〜0.17〜Hz 近辺)まで必要になることも、あると思われます。
それよりも緩い制御を行う場合もあると考えられますが、そのような場合には、定量的な検討を行う必要性は、少ないと考えられます。
上記は、P動作の制御ですが、実際には、PI、PID 動作を使用するでしょう。その他、各種の誤差や、ゆとりも必要ですから、これらを見込む必要があります。
◆ 以上を総合して、次の結論を導くことができます。
「制御系の解析、設計に必要な、制御対象の周波数応答の周波数帯域は、その一巡伝達関数の、安定限界付近の周波数である」 (図 3-2-13)。
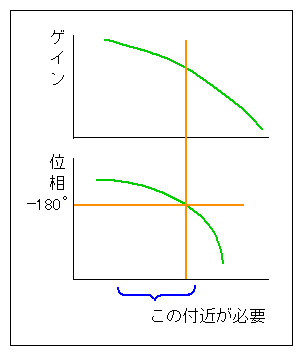
◆ さらに具体的にいえば、
「制御対象を、P 動作で制御したときの、安定限界の周波数から、その周波数より 1 decade 低い周波数の範囲に対して、上下に余裕を持たせたもの」
ということになります。
逆にいうと、制御系の解析、設計には、上記の周波数帯域の情報があれば十分です。その範囲外の情報は不要です。
ただし、場合によっては、静特性のゲイン(伝達関数で、s = 0 と置いたもの(コラム 3-2-3 参照))が必要になることがあります。