◆ PID 制御の概略の評価は 1.6 で行いました。ここでは、さらに定量的に評価を行います。
◆ P 動作においては、オフセットをゼロにすることはできません。P 動作では、オフセット の大きさが最も重要です。
図 3-2-35 の制御系において、目標値変化に対しては式 3-2-4、外乱入力に対しては式 3-2-5 が成立します。
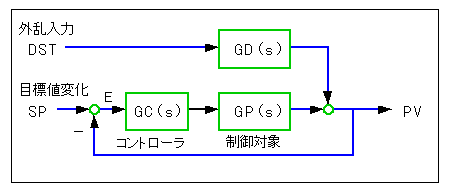
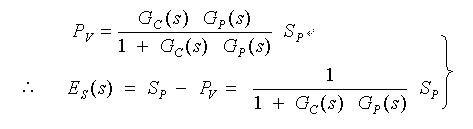・・・ (3-2-4)
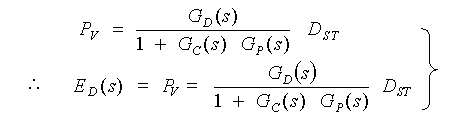・・・ (3-2-5)
◆ ここで、ES は目標値変化に対する偏差です。ED は外乱に対する偏差です。
これらの偏差は絶対値です。これを相対的な値に換算します。
目標値については、目標値変化(Sp)に対する割合をとります。
外乱については、無制御のときに外乱入力に対して発生する変化の大きさ(GC(s)・DST)に対する割合で考えます。
相対値を、それぞれESR、EDR
とすれば、
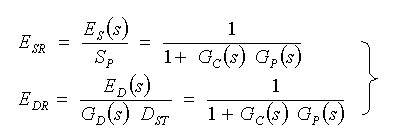・・・ (3-2-6)
となり、目標値に対しても外乱に対しても、等しくなります。したがって、両者を区別する必要がありませんから、サフィックス S と D を外して、相対偏差 ERを定義することができます。
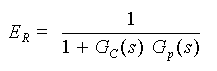・・・・ (3-2-7)
◆ オフセットは定常状態における偏差の値です。定常値は、伝達関数において、s → 0 とすることによって、求めることができます (コラム3-2-3 参照)。式 3-2-6 で、s → 0 と置いたものが、相対オフセット EF です。
P 動作は、GC(s) = KP ですから、P 動作の相対オフセット EFP は、
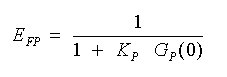・・・・ (3-2-8)
となります。
これが P 動作の制御効果です。ここで GP(0) は静特性のゲインです。相対オフセットの大きさは、静特性のゲイン GP(0) と、コントローラの比例ゲイン KP とに依存し、それらの値が大きいほど、相対オフセットは小さくなります。
比例ゲイン KP は、制御応答の減衰率によって制約されます。その減衰率は、制御対象の特性によって制約されます。
したがってオフットの大きさは、最終的には、制御対象の特性に支配されることになります。
[注] 相対偏差 ER と相対オフセット EF は、コントローラの客観的な評価に適しています。しかし、実際の制御では、絶対値の偏差 (ES または ED) とオフセット (ES(0) または ED(0)) の方が重要です。
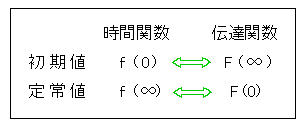
★ 時間領域の関数 f(t) において、その初期値 は時間 t = 0 と置いた f(0) です。定常状態は、時間が十分に経過したときの状態ですから、定常値 は
t = ∞ と置いた f(∞) となります。
★ 伝達関数のときはどうなるのでしょうか。伝達関数はラプラス変換領域で、F(s) で表わされます。
ラプラス変換の定義式は、式 3-1-1に示しました。時間 t とラプラス変換子 s が指数のところに積の形で入っています。
exp ( - s t )
★ 指数部の数は無次元数でなければなりません。無次元数とは、単位を持たない数のことです。
ここで、時間 t は時間の次元を持つ数です。指数部が無次元数であるためには、ラプラス変換子 s は、時間の逆数の次元(単位) でなければなリません。
★ したがって、時間領域 t → 0 に対応する、ラプラス変換領域は s → ∞です。また、時間領域 t → ∞ に対応する、ラプラス変換領域は s → 0 となります。
★ 以上から、次の関係が導かれます。
◆ 行き過ぎを許容するときの最適な制御応答は、振動的になります。この振動の周波数は、安定限界における持続振動の周波数よりも若干低い周波数です。
P 動作における、安定限界の振動周波数は、制御対象の特性だけから決まり、コントローラは関与できません。P 動作においては、3.2.2.(2) 図 3-2-9に示すように、一巡伝達関数の位相は、制御対象の特性によってのみ決まります。そして、それによって安定限界の振動周波数が決まってしまうからです。
したがって、P 動作においては、比例ゲイン KP の値を調整して、最適な、減衰率にすることはできますが、それ以上のことはできません。
このことも、オフセットと並んで、P 動作の限界です。
3.1.1.(2) で、「遅れ」について述べました。この遅れが、制御応答を決める要因です。
遅れを定量的に評価する値として、安定限界の振動周波数 fs の逆数(Ts = 1/fs)を取ることが、適切と考えられます。これを、安定限界周期 と呼ぶことにします。
◆ PI 動作は、P 動作の欠点を補って、オフセットをなくす効果があります。PI 動作の制御演算式は、
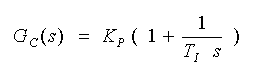・・・・ (3-2-9)
です。ここで KP は比例ゲイン、TI は積分時間です。オフセット EFI は、3.2.4.(1-A)式 3-2-6、7 から
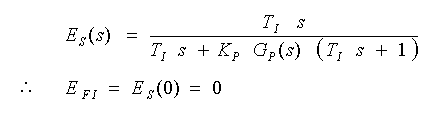・・・ (3-2-10)
となり、オフセットはゼロとなります。
◆ PI 動作の周波数応答を図 3-2-36 に示します。
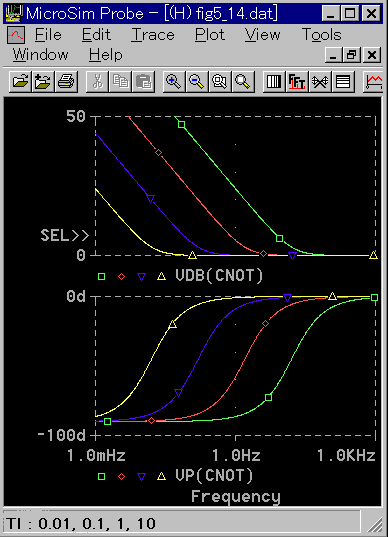
◆ 周波数が高いところではゲインは一定ですが、周波数が低いところでは周波数に反比例してゲインが高くなっています。この境界の周波数 fc は、
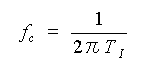・・・・ (3-2-11)
です。この境界周波数は、フィルタにおけるカットオフ周波数と同様なものです。
◆ P 動作の制御から推定されるように、ゲインが高いほど制御がよく効き、オフセットが小さくなります。PI 動作のゲインには周波数特性があります。
すなわち、周波数によってオフセットを減少させる能力が異なります。
PI 動作では、積分時間 TI を変えると図 3-2-36 に示したように周波数特性が変化します。
積分時間 TI を短くすることによって、高い周波数までゲインを高くすれば、より高い周波数までよく制御されて、より速やかにオフセットが減少します( 1.6.(3-A) 図 1-31、図 1-32)。
ただし、積分時間をさらに短くして、一巡伝達関数の位相が -180°になる周波数の近くでのゲインを、高くしてしまうと、安定度の問題に引っかかり、振動が激しくなります。
したがって、これに引っかからない範囲で、積分時間 TI をできるだけ短くするのが、最適な応答です。
最適な応答を求めるには、2乗誤差面積を利用できます。また、実用的な目安として、下記の方法があります。
行き過ぎを許容する場合、最適な制御応答では、振幅の減衰率が約1/4です。これは、振動の山が 3 番目までは観測され、4 番目の山は、ほとんど見えない程度の減衰です。
積分によるオフセットの現象も、同様に、振動の 3 山目ぐらいで目立たない程度に収まるのが、ちょうど適切と考えられます。
◆ 以上、PI 動作のゲインに注目して、PI 動作の効能を検討しました。今度は位相を見てみましょう。PI 動作は、それ自体で、最高 -90°の遅れがあります。これは、一巡伝達関数の位相遅れを増加させます (図 3-2-37)。
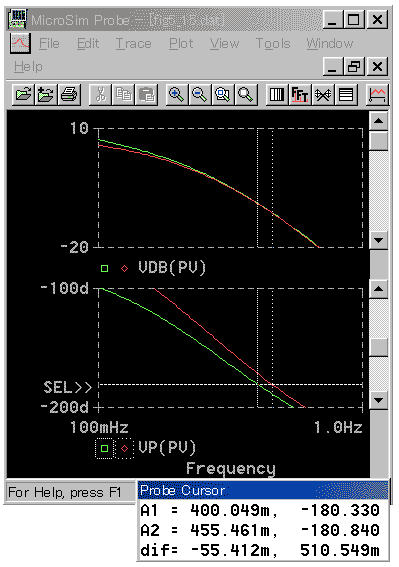
◆ その結果、P 動作と比較して安定限界の周波数が低くなります。図のカーソルから読み取ると、P 動作で約 455mHz のものが、PI 動作では約 400mHz に落ちています。この分、制御応答が悪くなる筈です。これをステップ応答で見ると、図 3-2-38 のようになります。
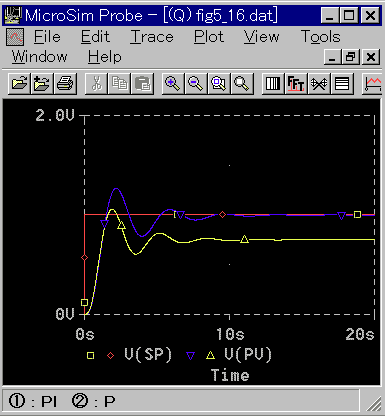
◆ 以上から、PI 動作にはオフセットをなくすという、優れた効能がありますが、その代償として制御応答が遅くなるという、副作用があることが分かります。通常は、効能の方が大きいので、副作用の方は我慢しているわけです。なお、この副作用は、次に示す微分動作で取り戻すことができます。
[ケース・スタディ 3-2-1]
(a) 図 3-2-38では、比較を分かりやすくするために、P 動作の比例ゲイン KP を、PI 動作と同じ値にしています。このため、PI 動作よりも振動の減衰率が大きくなっています。
振動の減衰率を PI 動作と同じ程度にすれば、P 動作の応答はさらに速くなるはずです。これを試みてください。
(b) 制御対象の特性が制御しやすい特性であれば、P 動作だけでもオフセットの値は小さくなります。
制御対象の特性を変えて、P 動作と PI 動作の一巡伝達関数とステップ応答をケース・スタディしてください。制御対象の特性は、制御対象の TDH と TCH を連動させて変えるのが良いでしょう。
◆ I 動作は単独で制御能力があり、オフセットをゼロにします。しかし、P 動作と組み合わせた PI 動作に比べて制御応答が悪いので、単独で、使用使用することはありません。
PI 動作として使用します ( 1.6.(3-B) 図1-33)。
I 動作単独の周波数応答を図 3-2-39 に示します。
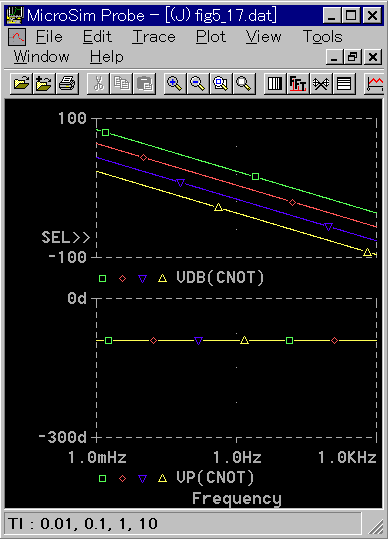
◆ 位相の遅れが、全周波数に対して -90°です。これは PI 動作よりも大きな遅れです。一巡伝達関数の位相遅れを、より一層増加させます。制御応答が PI 動作よりも悪い原因が、ここにあります。
