


◆ 先ず、ステップ応答によって、ディジタル制御の特性を調べて見ます。出力処理との組み合わせです。
◆ 図 4-2-2 は、基本式による、PID 制御のステップ応答です。
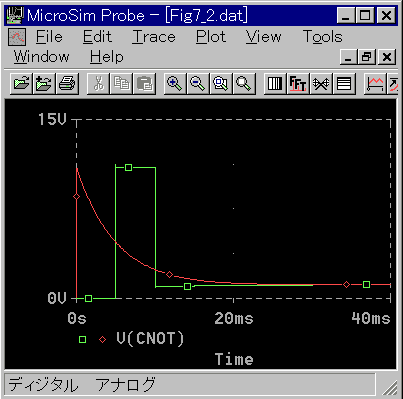
◆ 出力は、次回出力形です。この講座では、以降、原則として次回出力形を使用します。次回出力形は、最も遅れが大きいので、制御成績も悪くなります。
この意味では、ディジタル制御に対して厳しい評価になります。しかし、現実には次回出力形を、 使用しなけばならないことが多いのです。
比較のために、アナログ PID (時間領域形)の応答も示してあります。
[注1]
時間領域形のアナログ PID の制御演算式は、フィルタを含む 式 3-2-19 です。
[注2] 以降、ディジタル制御で、次回出力形のときは、これを明示しません。また、アナログ制御は、断らなければ、周波数領域形(含むフィルタ)です。
◆ 積分時間 TI と微分時間 TD の比は TI / TD = 4 です。これはアナログ PID 制御における限界感度法による最適応答時の条件です3.3.2.(2-F)表 3-3-1)。
サンプリング周期 TS は、TD / TS = 10 になっています。
微分効果は、最初に発生するパルスです。予想したように、微分はフィルタが無いのに、有限の高さと幅を持つパルスになっています。
これは、サンプリングが、フィルタの役割を果たしているからです。アナログと波形は大きく異なりますが、同等の効果を持っているような感じです。
ただし、ディジタルは、パルスが 1 サンプル分遅れています。この遅れは、微分効果を減殺しているはずです。
この図には示されていませんが、同時出力形では、1 サンプル分の遅れはありません(4.1.3.(3-B-a) 図 4-1-19 は同時出力形です)。同時出力形の方が、微分効果が大きいはずです。
積分効果は、この図では良く分かりません。次の(1-C)で調べます。
◆ サンプリング周期を変えたときの応答を図 4-2-3に示します。
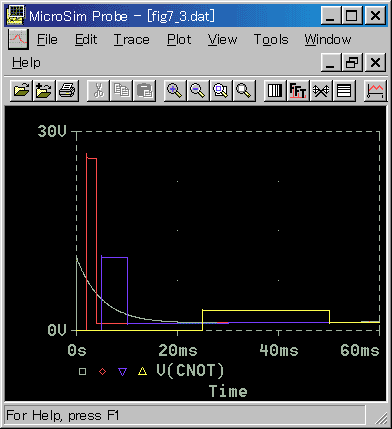
◆ TS は、サンプリング周期です。サンプリング周期が長いとき、微分は効果が無くなるであろうことが推測されます。
サンプリング周期が、非常に短いと、パルスの高さが極端に高くなることが予想されます。これは、真の微分に近くなることを意味します。それによる問題がありそうです。
◆ 微分パルスの後には、積分の特性が現われています。図 4-2-2 では、よく分からないので、図 4-2-3 の 1 部分を拡大したのが、図 4-2-4 です。
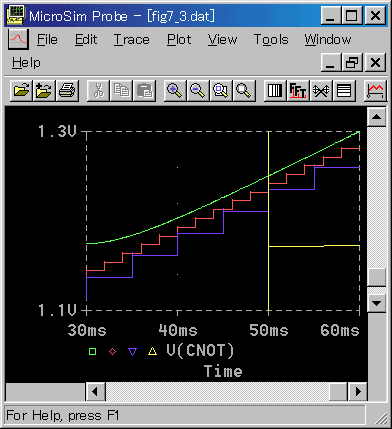
◆ 積分も、サンプリング周期の影響はありますが、微分のような激しい現象はありません。サンプリング周期が長くなると、遅れは大きくなりますが、積分の特性が、そのまま表われています。
同時出力形であれば、ディジタル出力は、アナログの値を跨ぐはずです(4.1.3.(3-B-b) 図 4-1-21))。跨がないで遅れているのは、次回出力形のためです。
[注] 図の黄色は、微分パルスの終わりの部分です。積分の特性は、この後に現われます。
[コラム 4-2-1] 積分の制御演算式に 式 4-1-17 を使う
★ 上記の、次回出力形の遅れを、多少でも取り戻す方法として、積分の演算に、式 4-1-18 の代わりに、式 4-1-17 を使用することが考えられます。式 4-1-17 を使用した波形を示します。
![[注]の図 1](cont42/fg4_2_11c.gif)
★ 図から分かるように、アナログを跨ぐことにはなりませんが、改善は、されています。ただし、この特性の改善は、制御応答の改善には役立ちません。
サンプリング周期が短い(TI / TS が大きい)ときは、制御応答の差は、ほとんどありません。
★ TI / TS が小さいときは、制御応答に差が現われます。ただし、この差は、比例ゲイン KP が大きくなったのと同等に作用します。
図を見ると、ディジタルの制御出力が、上方に移動した形になっています。これは、比例ゲイン KP を大きくしたことを意味します。
★ 制御応答を見てみましょう。
![[注]の図 2](cont42/fg4_2_12c.gif)
★ この図は、共に、PI 動作 TI/TS = 2 です。この条件では、上記の、比例ゲイン KP が大きくなった効果が現われて、式 4-1-18 は、振動が激しくなっています。
そこで、比例ゲイン KP が同等に働くように、比例ゲイン KP を調整したのが、修正です。
★ 式 4-1-17 を使用したことによって、積分動作が、比例動作に影響を及ぼすようになります。これは、パラメータ間に干渉があるということです(3.2.4.(4-C))。
★ この講座で、積分動作に、式 4-1-18 を選んだ理由の1 つに、パラメータの独立性があります。
[ケーススタディ 4-2-1]
★ このケーススタディは、シミュレーションに興味のある人が行って下さい。
基本式で、積分を、式 4-1-17 に置き換えたコントローラは、PIDTA の名で、ライブラリ cont.lib に入っています。
★ これを使用して、式 4-1-17 と、式 4-1-18 の違いを、自由に試みてください。
★ ディジタル制御においては、制御演算を、ソフトウェアで行います。このソフトウェア・プログラムは、パルス伝達関数を、時間領域に変換すれば、ほとんどそのまま利用することができます。
★ この時間領域への変換は、簡単です。式 4-1-15 の逆向きを実行するだけです。たとえば、パルス伝達関数が、
( 1 + K1 z-1 + K2 z-2 )
のときは、
Y(z) = ( 1 + K1 z-1 + K2 z-2 ) X(z)
ですから、
Y(z) = ( X(z) + z-1 X(z) + K2 z-2 X(z) )
∴ yi = xi + K1 xi-1 + K2 xi-2
となります。
★ ただし、分数になっているところは、分母の部分を、次のように変形します。たとえば、
1 / ( 1 + K z-1 )
X(z) = Y(z) / ( 1 + K z-1 )
Y(z) = ( 1 + K z-1 ) X(z)
yi = xi + K xi-1
となります。
★ また、パルス伝達関数の掛け算は、時間領域ではカスケード接続です(3.1.1 図 3-1-11 (11)の逆向き)。すなわち、
W(z) = X(z) Y(z)
wi = xi , xi = yi
wi = xi( yi )
です。
◆ サブサーキット PIDTP と、ディレイアンドホールド DAHT を組み合わせて、実用式のステップ応答を調べて見ます(図 4-2-5)。
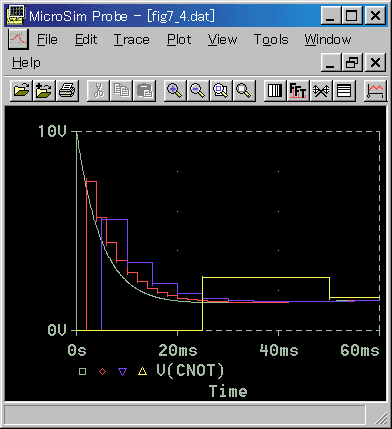
◆ サンプリング周期を変えてその応答を比較しています。サンプリング周期が短いときは、アナログ制御と同等な特性を持っています。フィルタが入っていますから、基本式のような問題はありません。
これはフィルタの効能ですから、時間領域形の基本式においても、フィルタを入れれば、実用式と、ほとんど同じになるはずです。
サンプリング周期を長くすると、アナログの特性からは大きく異なり、むしろ基本式に近くなります。そして、サンプリング周期が長くなるのにともなって、その特性が劣化しています。
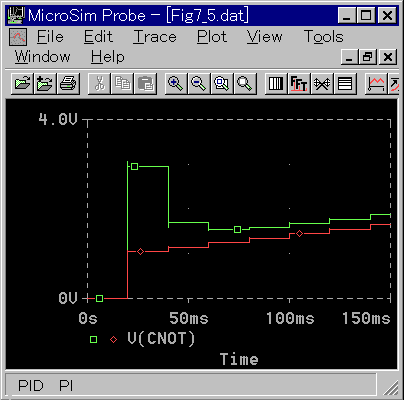
◆ しかし、同じサンプリング周期(25ms)の PI 動作と比較すれば、図 4-2-6 に示すように、微分動作を付加したことによる違いは、かなりあります。それなりの効果は期待できるかも知れません(4.2.3.(3-B)参照)。
◆ ディジタル制御では、サンプルアンドホールドがあります。サンプルアンドホールドは、ステップ応答波形に最も良く現れます。この意味では、ステップ応答は、アナログよりも重要な意味を持っています。
しかし、より細かな特性の差を表わすという意味では、ディジタル制御においても、周波数応答が優れています。