


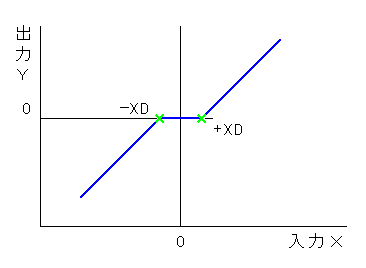
◆ 機械系には、ガタがあります。このガタは、通常、不感帯と呼ばれる非線形特性です。不感帯 の特性を図 5-30 に示します。
◆ だだし実際には、ガタは、この不感帯ではなく、次に示すヒステリシスであることが多いのです。
ガタは、コントローラにも存在しますが、むしろ制御対象にあるガタが問題になります。一般にガタの存在は、制御成績を低下させる方向に働きます。
毒も使い様によっては薬になります。
とくにディジタル制御においては、制御成績改善のために、故意にコントローラに不感帯を持たせることがあります(5.5.(4-D)参照)。
◆ この不感帯は、アナログ・ビヘ-ビア・モデルのテーブルによる表現(5.5.(2-C-a))によって作ることができます。
不感帯の記号を図 5-30のように取ると、その書式は、
E<名称> Y 0 TABLE{X}=(-(1MEG+XD), -1MEG) (-XD, 0) (XD, 0) ((1MEG+XD), 1MEG)
( < > は、必須 [ ] は、省略可能 *は、繰り返し可能)
です。
不感帯も、便利に使用できるサブサーキット DEDZN を用意しました。書式は、
* 出力 入力 高不感帯幅 低不感帯幅 .SUBCKT DEDZN OT IN PARAMS: VH=0 VL=0
です。
リミッタ LIMIT と同じ形式で、OT : 出力、IN : 入力、VH : 高側不感帯幅電圧、VL : 低側不感帯幅電圧です。デフォルトは、不感帯無しです。
入力からリミッタ特性を引き算すると、不感帯になります。サブサーキットも、このようになっています。
[注] ただし、不感帯無しを指定しても、不感帯は完全にはゼロになりません。2mV 程度の不感帯があります。
◆ 実際のガタは、多くがヒステリシスです。ヒステリシス 特性を図 5-31 に示します。
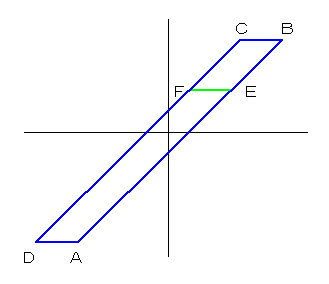
◆ いま A 点から出発し、入力が増加して B 点まで行ったとき、入力が減少し始めたとします。
ヒステリシスが無ければ、再び B-A 線上を戻ります。
ところが、ヒステリシスがあるときは、入力が減少しても、しばらくの間は出力が変化しません。
一定の幅 B-C だけ入力が減少してから、始めて出力が減少し始め、C-D 線上をたどります。
D 点で、入力が減少から増加に変わると、D-A-B のように変化します。
結果的に、軌跡は平行四辺形になります。
もし、入力が、A から B に行く途中、たとえば E 点で、減少に転じたとすれば、E-F-D の経路を取ります。
任意の位置で入力の変化方向が反転すると、その位置から一定の幅の間は、入力が変化しても出力が変化しません。入力がそれ以上変化して始めて出力が変化し始めます。
◆ 実際のガタは、前回動作を停止した時の状況と今回動き始めるときとの関係によって、今回の動き始めの状況が異なります。
すなわち図 5-32 の(a)から(c)の範囲で変化します。
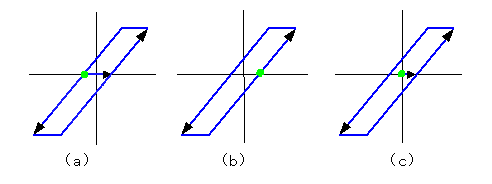
◆ どの図も今回のスタートは ● 印です。
(a) は、前回は、今回と逆方向に動いていて停止したときです。(b) は、前回と同方向に動き始めた場合です。
前回停止するときに、ヒステリシス幅の途中で停止したときは、(c) になります。(c) は、必ずしも原点ではなく、(a) と (b) の中間の任意の点が起点になります。
どのようにタートするかは、前回の状況が常に一定である場合を除き、毎回異なります。
制御を行なっている場合には、制御応答波形も異なります。
しかしガタが小さいときは、始動状況の差は、制御応答にはほとんど現れません。通常ガタは小さいので、制御応答は、始動点の違いを無視することができます。
◆ ヒステリシスも、サブサーキットを用意しました。サブサーキットの書式は、
* 出力 入力 ヒステリシス幅 時定数 .SUBCKT HSTRS OT IN PARAMS: HW=1 TC=1M
で、OT : 出力、 IN : 入力、 HW : ヒステリシス幅(全幅:図 5-24 の FE)、TC = 時定数です。
ヒステリシスは、静特性ですから、本来遅れは存在しません。しかし、系全体の遅れに対応した大きさの遅れが、ヒステリシスのサブサーキット内に入っていないと、シミュレーションがエラーになります。
エラーの発生を防ぐために、遅れ TC を入れてあります。
TC の値が大き過ぎると、遅れによる誤差が発生します。エラーが発生しない程度に TC の値を決めます。
◆ サブサーキットの特性を図 5-33に示します。
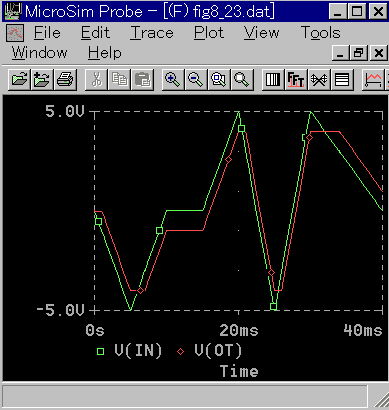
◆ 図から分かるように、このモデルは図 5-32 (c) の特性を持っています。
通常は、ヒステリシスの幅は小さいので、5.5.(4-B-a)に示したように、全てのヒステリシスに使用することができます。
シミュレーションモデルの概要を、図 5-34 に示します。
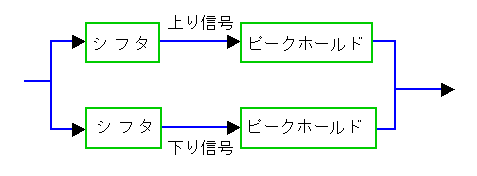
◆ ヒステリシスは、上りと下りとで経路が違います。シフタによって上りの線と、下りの線を作っています。
ピークホールドは、信号が上昇から下降に変わるとき、またはその逆のとき、ピーク値をホールドする回路です。ダイオードの特性を利用しています。
◆ ヒステリシスを含む制御対象を制御したときの応答を、図 5-35 に示します。PID パラメータの値は、ヒステリシスを含まないときの最適条件です。
[図 5-35] ヒステリシス付制御対象の制御(ヒステリシス幅変化)
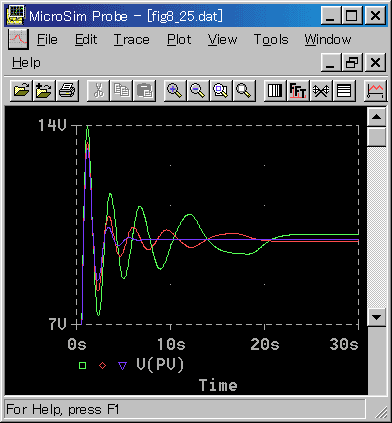
◆ ヒステリシスは、コントローラと制御対象(線形部分)との間に入れてあります。
ヒステリシスは、アクチュエータなど、制御対象の最初の部分に存在することが多いので、これを模擬したものです。
ヒステリシス幅が広いほど遅れが大きく、制御成績が悪くなります。
ヒステリシス幅が広い方が、より振動的ですが、波形は、線形系のように単純ではありません。
制御変数の振幅が大きいところでは、ヒステリシス幅が相対的に小さいので、ヒステリシスの影響は小さく、制御変数の振幅が小さいところでヒステリシスの影響が大きく現われます。
このため、振幅が小さい部分の振動が、なかなか減衰しません。
◆ 図 5-36 は、ヒステリシス幅 = 10 のときの、コントローラ出力(CNOT)と、ヒステリシス後(OT)の波形を示します。
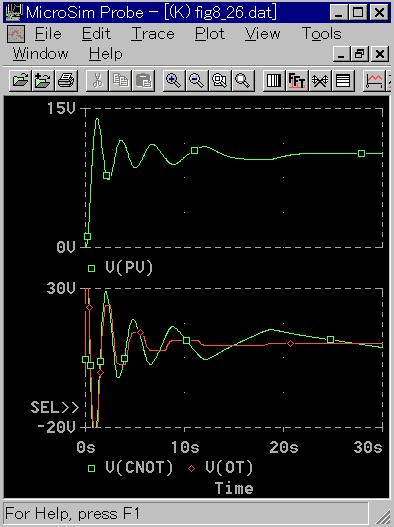
◆ ヒステリシス特性が、良く現われています。
以上、ヒステリシスによる、制御応答の悪化を要約すると、次の通りです。
◆ したがって、制御ループの中に、ヒステリシスを入れないように、やむを得ず入る場合には、できる限り小さくすることが重要です。
◆ 比例ゲイン KP の値を変化させて見ましょう (図 5-37)。
[図 5-37] ヒステリシス付制御対象の制御(KP 変化)
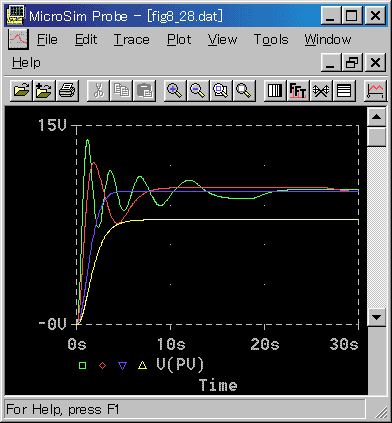
◆ 比例ゲイン KP = 4.4 は、元 (図 5-35) の値です。KP を小さくすれば、振動の振幅は小さくなり、周波数は低くなります。さらに比例ゲインを小さくすれば非振動的になります。この変化は、定性的には線形系と同じ傾向です。
なお、KP = 0.2 のときも、時間が経てば偏差は正常値になります(図 5-38)。
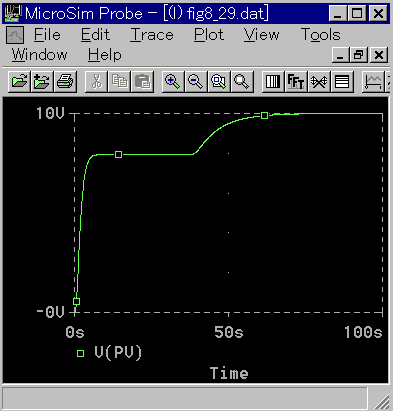
◆ 今度は、積分時間を変えてます(図 5-39)。
[図 5-39] ヒステリシス付制御対象の制御(積分時間変化)
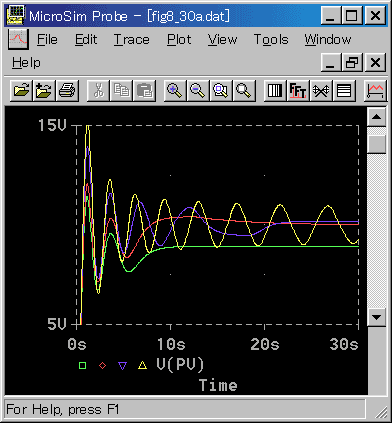
◆ これも変化の傾向は、線形系と同じです。TI = 20 も、時間が経てば、偏差は正常に戻ります。
以上のように、PIDパラメータを変化させたときの制御応答の変化は、複雑ですが、傾向として線形系と同じです。
ヒステリシスを含む系においても、トライアルを行なうことによって、そのシステムにマッチした波形に最適化することが可能です。
ただし、ヒステリシスにより、大幅に制御応答が悪化している、その枠内での最適化です。
◆ 制御対象の非線形性、とくにヒステリシスは、制御応答を悪化させます。したがって、ヒステリシスを無くす、できるだけ小さくすることが必要です。
しかし、どうしても、ヒステリシスを避けられない場合があります。このようなとき、少しでも、制御成績を改善できる方法として、不感帯を持つコントローラの利用があります。
不感帯は、偏差のところに入れます(図 5-40)。

◆ PID コントローラ PIDAに不感帯を挿入した、アナログモデルのサブサーキット PIDAD を用意しました。書式は、PIDA とほとんど同じで、パラメータに不感帯幅 DB (全幅は ±DB )を追加したものです。
* 操作出力 目標値 制御変数 比例ゲイン 積分時間 微分時間 不感帯 .SUBCKT PIDAD CNOT SP PV PARAMS: KP=1 TI=1MEG TD=0 DB=0
◆ このコントローラを使用して、ヒステリシスによる遅れを改善した例を、図 5-41 に示します。
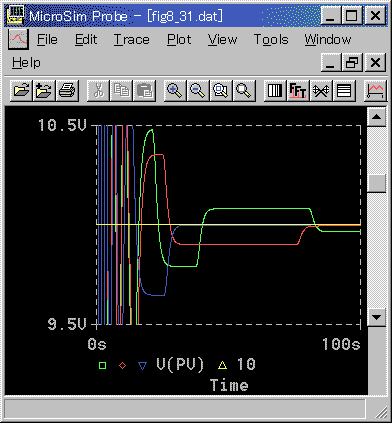
◆ 制御対象のヒステリシス幅は 10 で、図 5-33 の緑と同じです。ステップ応答のステップ幅は 10 ですから、不感帯の大きさは、十分小さい値です。それで十分な効果が現われています。
非線形のモデルは、色々細工してあります。したがって、再現性や安定性には欠ける面があります。
たとえば、上記のシミュレーションモデルには、ヒステリシスと、不感帯の 2 つの非線形が入っています。このため、図 5-41 と同じ条件で、時間軸だけを変えた図 5-42 は、
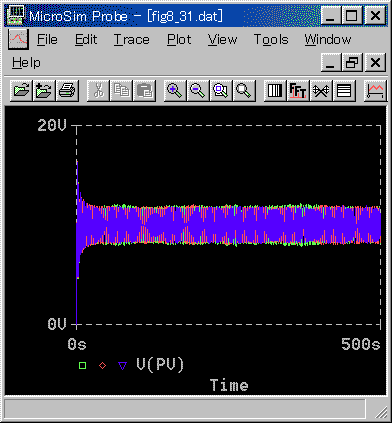
◆ 図のように、発振しています。
このように、完全に、おかしくなっていれば、すぐ分かります。しかし、一見まともなことも多いので、注意してください(コラム 2-2-3、コラム 2-2-4参照)。
◆ コントローラに不感帯を入れた実例を紹介します。図 5-16 と場所は異なりますが、流量制御系の例です。アナログ制御を図 5-43 に、ディジタル制御に交換したときを図 5-44 に示します。
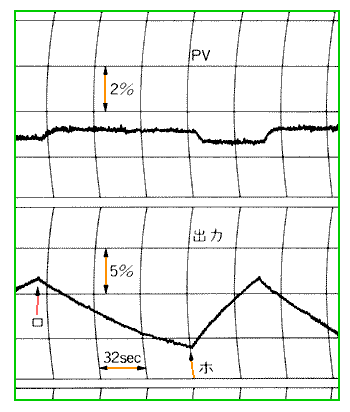
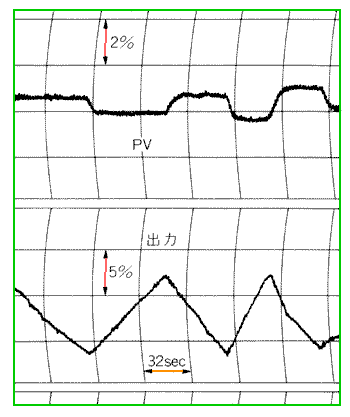
◆ どちらもハンチングしています。大体同じですが、ディジタルの方が、振幅が大きくなっています。
通常の流量制御系では、このようなハンチングはありません。原因を調べて見ました。原因は、調節弁でした。この調節弁の特性を図 5-45 に示します。
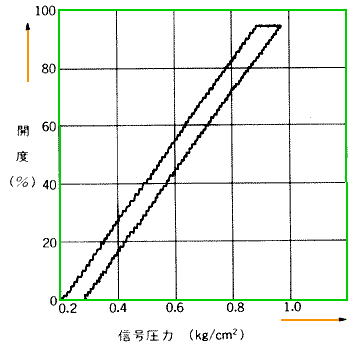
◆ この調節弁は、空気圧駆動なので、横軸は空気圧です。図から分かるように大きなヒステリシスがあります。
しかも普通のヒステリシスではなく、ガタ/ガタと階段状に動いています。高温高圧の油に使用しているので、摩擦が極端に大きく、このような特性なったものです。
ハンチングの原因は分かりましたが、アナログ制御とディジタル制御とで、差があります。
これは、サンプリング周期の問題ではありません。デイジタル制御の方が、忠実に値を出力してることに起因しています。アナログ回路の方が、出力値が曖昧です。それがかえって、制御成績を良くしていると考えられます。
そこで、ディジタル制御に不感帯をいれて見ました。その制御応答が、図 5-46 です。
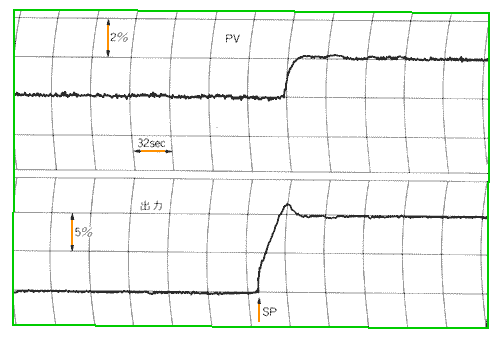
◆ 非常に良好な制御になりました。
ただし、不感帯幅が大き過ぎると。オフセットが発生します。ハンチングとオフセットとの兼ね合いが重要です。