◆ ディジタル制御系のハードウエア構成は、コントローラの入出力がアナログの場合と、ディジタルのとき、とがあります。
最近はディジタル化が進み、コントローラの入出力は、ディジタル方式が多くなっています。とくに、コントローラの操作出力は、以前からディジタル方式が多く利用されています。
これは 1.5.(4-B) に示した、操作部のディジタル化とも密接に関連しています。
最終的に制御対象に働きかける制御演算式は、所定の演算式でなければなりません。しかし、コントローらからは、別の形で出力して、操作部のところで所定の制御演算式に変換する方法も、あります。
ディジタル制御においては、この両方が使われています。これに対応して、コントローラの出力方式は、ポジションフォーム、およびベロシティフォームと呼ばれる、２ 種類の方式があります。
◆ コントローラからの出力が、最終的に制御対象に働きかける制御演算式と、等しいものを、ポジションフォーム と呼んでいます。
ディジタル制御では、コントローラからの出力が、アナログのものと、ディジタルのものとがあります(図 4-1-5)。
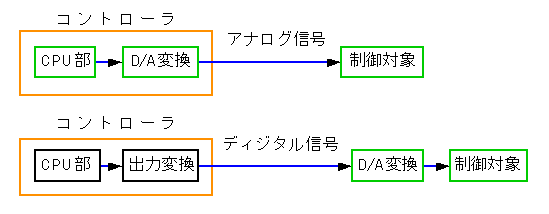
◆ アナログ制御は、もともと、ポジションフォームだけしかありません。ディジタル制御においても、アナログ出力形(図の上側)では、もっぱら、ポジションフォームが使われています。
◆ 制御対象からの入力は、サンプリングされた後に、制御演算を実行します。その演算結果を、コントローラから出力します(図 4-1-6)。
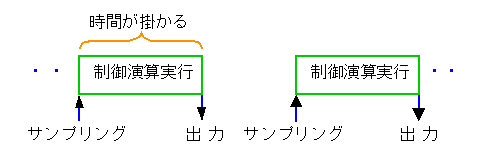
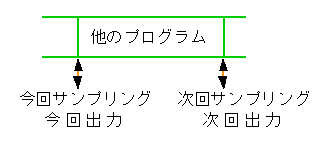
◆ コントローラの出力は、図のように、今回のサンプリングと次回のサンプリングとの、中間の時点で行ないます。
コンピュータをこのコントローラ専用に使っている場合には、コントローラから出力後、直ちに次ぎの入力を行ない、次ぎの演算に入ります。
近似的に、今回の出力時点と次回サンプリング時点とが、同時であると見なせます。これを次回出力形 と呼びます(図 4-1-7)。
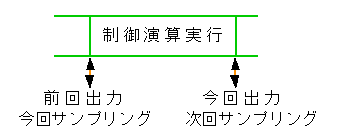
◆ 次回出力形を、制御演算式の形で表現すると、式 4-1-7 になります。
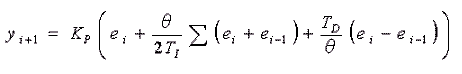・・・ (4-1-7)
コンピュータを他の用途に多く使っている場合には、制御演算の時間を無視できて、今回のサンプリングの時点で出力していると、見なすことができる場合もあります。
これを同時出力形 と言います(図 4-1-8)。
◆ 同時出力形の制御演算式は、式 4-1-5 そのものです。
実際には、図 4-1-6 のように、サンプリングの中間で出力している、と見なさなければならない場合もあります。これを中間出力形 と呼びます。
従来は、実際は中間出力形であっても、次回出力形または同時出力形の、どちらかで近似していました。これは、中間の出力を取り扱うことが、理論的には面倒だからです。
しかしシミュレーションを利用するなら、サンプリングの中間における、任意のタイミングで出力させることは、容易です。
◆ アナログの制御においては、遅れは制御成績を悪くする要因でした。たとえば、制御対象の特性を 1 次遅れ + むだ時間 としたとき、むだ時間が大きいほど、制御成績は悪くなります(3.3.3.(1))。
ディジタル制御においても、この点は同様です。ディジタル制御では、アナログ制御における遅れの要因に対して、さらにサンプリングによる遅れが付け加わります。
この意味では、同時出力形が望ましいわけです。しかし実際には多くの場合、同時出力形にすることは、困難です。現実には、次回出力形を、使用しなければならないケースが、多いのです。
この理由から、理論上は、ディジタル制御の制御演算式として、次回出力形に対応する、式 4-1-7 が多く使用されています。
◆ コントローラからの出力がディジタルのとき(4.1.2.(4-B-a))は、ベロシティフォームが多く使用されています。
ベロシティフォーム では、コントローラからは、ポジションフォームの制御演算式を、差分したものを出力します。したがって操作部のところで、加算を行なって元の式に戻します(図 4-1-9)。
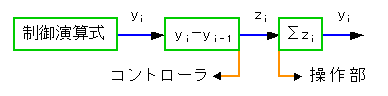
◆ 操作部がアナログの場合は、この後に D/A 変換器を設けます。yi はポジションフォーム、zi はベロシティフォームの出力です。
ベロシティフォームの名は、位置(ポジション)を微分すると速度(ベロシティ)になるところから付けられたものです。しかし実際には、単に差を取っているのであって、微分しているのではありません。
式 4-1-5 のポジションフォームの PID 制御に対応する、ベロシティフォームの制御演算式は、
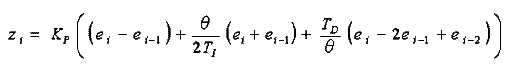・・・ (4-1-8)
です。
◆ ベロシティフォームのコントローラ出力は、ディジタルですが、2 進数などのコード出力は、あまり多くは使われていません。パルス数出力が多く使われています。パルス数出力は、数値をパルスの数で表わしたものです。
パルス数出力は、コード出力よりも、作成、伝送が容易です。しかも、操作部における加算は、単にカウンタを使用すればよく、この点でも有利です。
アクチュエータにステッピングモータを使用するときは、パルス数出力をステッピングモータに直接加えることができます。このときはステッピングモータが、ベロシティフォームの加算器、D/A変換器、アクチュエータの三つの機能を兼ねています。
この他、ベロシティフォームは、細かい点でポジションフォームより優れている点がいくつかあります。したがって、デイジタル制御では、ベロシティフォームが、多く使用されています。
◆ ベロシティフォームの制御対象への最終出力は、ポジションフォームと同じです。この意味では、ポジションフォームと変わるところはありません。
したがって、実際にはベロシティフォームを使用していても、制御系の解析・設計は、通常はポジションフォームとして行ないます。
ただしベロシティフォームは、遅れを考えなければならない場合があります。
ポジションフォームは、出力のタイミングで直ちに出力します。これに対してパルス数出力は、パルスを逐次出力します。パルスを出し終わるまでに時間が掛かります(図 4-1-10)。
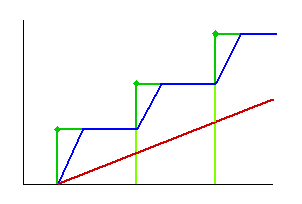
◆ 図において、ポジションフォームの制御演算結果が、黒丸のようになっているとき、ポジションフォームの最終出力（ホールド出力）は黒線のようになります。
パルス数出力は、出力に時間が掛かります。それをカウントした最終出力は、青線のようになります。ただしパルス速度が充分速ければ、立ち上がりも充分に速く、遅れは無視できます。
パルス速度が極端に遅いと、図の茶色のようなことも起こります。このときは、遅れによる積み残し(図の緑色)が発生します。
この積み残しが切り捨てられるようになっている場合には、単に遅れるだけでなく、切捨てによる出力の誤差が発生します。出力の誤差が発生すると、制御に悪影響があります。
遅れの問題は、ポジションフォームでも発生します。コントローラ出力が十分速くても、アクチュエータに大きな遅れがあれば、この遅れを無視できません。
以上の問題はありますが、操作出力と操作部とが十分な速度に設計されていれば、ベロシティフォームの制御特性は、ポジションフォームと同等です。通常は、そのように、システムを構成します。
◆ ベロシティフォームの出力は、通常はコンピュータの演算処理と並行して行ないます(図 4-1-11)。
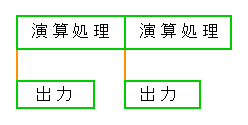
◆ 専用のハードウェアを使用することが多く、この場合はコンピュータの演算に影響を与えません。
出力開始のタイミングは、ポジションフォームと同様に、同時出力形、中間出力形、次回出力形があります。
◆ ベロシティフォームが有用なのは、コントローラからの出力です。コントローラ内の制御演算は、ベロシティフォームを使用することの利点はありません。
制御演算の実行自体は、ポジションフォームでもベロシティフォームでも、大差ありません。しかし分かりやすさの点で、ポジションフォームの方が優れています。
通常は、ポジションフォームで制御演算を行い、最後の出力のところで、ベロシティフォームに変換します(図 4-1-12)。
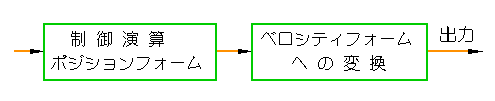
◆ ここでサンプリングの特性について、説明しておきます。
◆ サンプリングによって、アナログの情報が失われます(4.1.1.(2))。これを定量的に示したのが、サンプリング定理 です。
アナログの任意波形 x(t) の信号は、周波数が異なる多数の正弦波形の和、で表わされます(図 4-1-13)。
[図 4-1-13] 任意波形は多数の正弦波形の和で表わされる
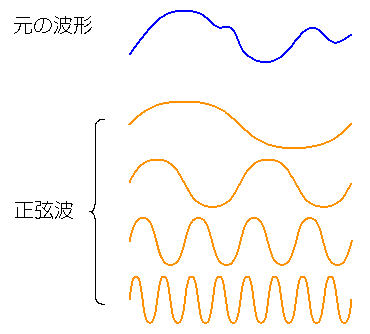
◆ これを式の形で表わすと
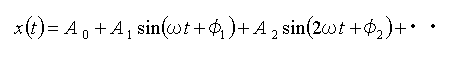・・・ (4-1-9)
となります。
サンプリング定理は、
「ある波形が持っている周波数 f 以下の情報を、サンプリングによって失わないようにするためには、サンプリング周波数は、2f 以上でなければならない。」
というものです。
図 4-1-14 は、正弦波形を、その周波数の 2 倍のサンプリング周波数で、サンプリングしたときを示しています。
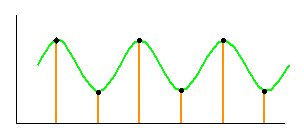
◆ この条件では、正弦波形の情報は、サンプリングしても保持されていることが分かります。サンプリング周波数をこれよりも低くすると、正弦波形の情報が得られなくなるであろうことは、感覚的に了解できると思います。
◆ サンプリングによって、サンプリング定理に違反した周波数の情報は失われてしまいます。失われて何も残らないのであれば、まだ良いのですが、そうはなりません。
元の信号には存在しなかった、アリアス (ニセの情報)をつかまされてしまいます。図 4-1-15 は、サンプリング定理に違反したサンプリングを行なったものです。
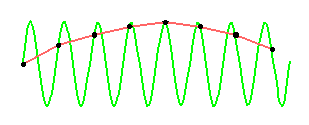
◆ サンプリングによって、元の周波数の情報は失われています。その代わりに、元の信号には存在しなかった、低い周波数の成分(黒線)が観測されます。これがアリアスです。
◆ 制御は、入力された情報を元にして実行されます。サンプリング定理に違反したアリアスであったとしても、それを見分けることはできません。それを正しいものとして制御を実行します。
その結果として、間違った制御を行ってしまいます。
サンプリング周期は、サンプリング定理に違反しないように、制御変数が持つ周波数帯域の、少なくとも 2 倍の周波数をカバーするように決める必要があります。
