◆ ディジタル系にも周波数応答が存在し、アナログ系と同様に、便利に利用することができます。ただし、アナログ系の周波数応答とは、定義が異なりますから、その点に注意する必要があります。
ディジタル系の周波数応答 は、図 4-1-28 のように定義されます。
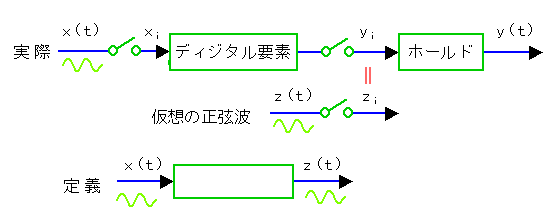
◆ アナログ入力のところに、正弦波形 x(t) を加えます。これがサンプリングされてサンプル値 xi となり、ディジタル要素を通過します。
ディジタル要素の出力 yi はサンプル値です。図のサンプリング記号は、実際にサンプリングしているのではなく、この場所がサンプル値であることを強調するためのものです(4.1.3.(1-B))。
このサンプル値 yi は、ホールドを通過すれば、アナログ値 y(t) になります。ただし周波数応答の定義には、このホールドは必須ではありません。
一方、実在しない仮想の正弦波 z(t) を考えます。そしてこの仮想の正弦波を、実在のシステムに同期してサンプリングします。
その出力を zi とすると、zi＝yi となるような、仮想の正弦波が存在します。
ディジタル系の周波数応答は、実際の正弦波入力 x(t) を入力とし、仮想の正弦波 z(t) を出力として定義されます。したがって、周波数応答はアナログ系で定義され、入出力ともに正弦波形です。
しかし実際のディジタル系はサンプル値です。正弦波形の周期に比べてサンプリング周期が十分に短いときは、近似的にアナログの周波数応答と同じになります。
サンプリングが粗いと、サンプル値は正弦波形とは大きく異なります。
◆ アナログ系の場合、伝達関数から周波数応答を計算することができました。しかも計算が簡単なことが大きな特徴でした。アナログ系では、伝達関数において、s=jω と置くことによって、直ちに周波数応答が求まりました(3.1.2.(3-C))。
デイジタル系においても、パルス伝達関数から、周波数応答を計算することができます。
パルス伝達関数は z の関数です。しかし式4-1-12 によって、パルス伝達関数は、アナログの伝達関数に戻すことができます。伝達関数であれば、周波数応答は直ちに求まります。
この周波数応答が、すなわち、ディジタル系の周波数応答です。したがって、パルス伝達関数において、式 4-1-22 のように置き換えることによって、周波数応答になります。
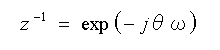・・・・ (4-1-22)
置き換えたものは、周波数伝達関数ですから、ボード線図を求める手順は、アナログと同じです(3.1.2(3-C))。
◆ このディジタルの周波数応答は、周期関数です。式 4-1-22 から分かるように、周波数応答は、exp(-jθω) の関数です。
この関数形が三角関数であることは、3.1.2.(3-B)で説明しました。ということは、周波数応答が周期関数だということです。すなわち (θω) が、0〜2π の周期関数です。
しかも、(θω) が 0〜π までの間と、π〜2π までの間とは、ゲインについては鏡面対称であるという、性質を持っています。したがって、周波数特性は、0〜π まで計算すれば十分です(図 4-1-29)。
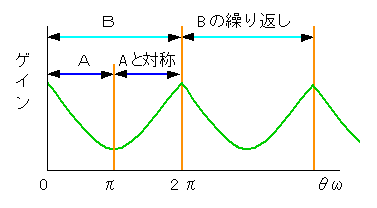
[注] この図は、繰り返し波形であることを示したものです。具体的な波形を示したものではありません。
◆ 位相についても、鏡面対称ではありませんが、対称性があり、これも 0〜π までの計算で十分です。
次に、(θω)=π の条件について考えて見ます。サンプリング周波数を fθ、信号周波数を fs とすれば、
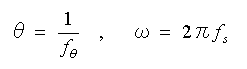・・・・ (4-1-23)
ですから、
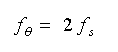・・・・ (4-1-24)
となります。すなわち、
・・・・ (4-1-25)
は、サンプリング定理ギリギリの条件であり、信号周波数がこれより高い所はサンプリング定理に違反します。
◆ 簡単な周波数応答の具体例を示します。
◆ ディジタル微分の周波数応答を見てみましょう(図 4-1-30)。回路ファイル (fg4_1_30.cir) の内容は、AC 解析になっていることと、アナログの微分が 1次遅れ無しの純粋な微分になっている点を除いては fg4_1_19.cir と同じです。
[注] 周波数応答では、純粋の微分をシミュレートすることができます(3.1.3.(5-B-a)。
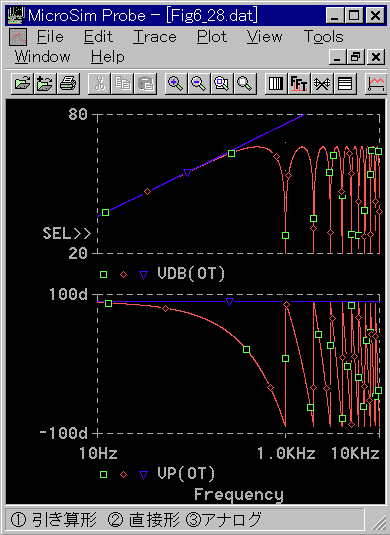
◆ ステップ応答と異なり、直接形も誤差はありません。ディジタルの周波数応答の一般的性質から、周期関数になっています。ただし周波数軸が対数ですですから、図 4-1-29 とは感じが違います。
低い周波数では、アナログと良く一致しています。しかし高い周波数で大きく違っています。ゲインが頭打ちになり、位相は 90°から大きく遅れています。
これは、ディジタル周波数応答の周期性に起因しています。それと、サンプリングがフィルタの役割を果たしていることです。
このことは、ディジタル制御においては、フィルタ無しの制御演算式が、実用になることを意味しています(4.2.1.(1-A)参照)。
◆ 積分には、式 4-1-17 と、式 4-1-18 の 2 種類があります。先ず、式 4-1-17 の方を、図 4-1-31 に示します。
[図 4-1-31] ディジタル積分(式 4-1-17)の周波数応答
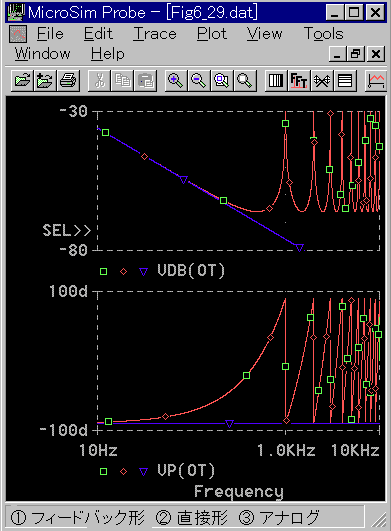
◆ 直接形とフィードバック形ともに正常に動作します。次に両式の比較を行ないます(図 4-1-32)。
[図 4-1-32] ディジタル積分)の周波数応答(両式の比較)
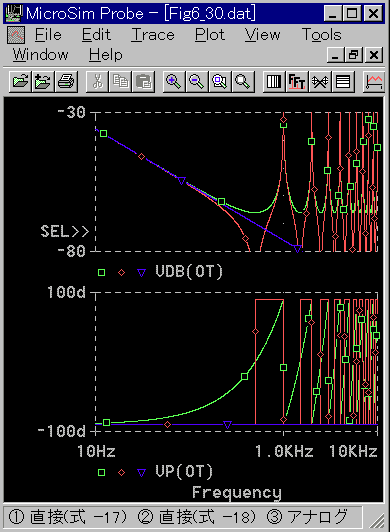
◆ どちらも、微分と同様に、低い周波数では、アナログと一致し、高周波数では、ずれています。両式を比較すると、一見、その優劣には、差がないように思われます。
しかし、一致性の評価は、周波数応答が意味を持つ範囲で行うべきです。意味を持つ範囲は、サンプリング定理に違反しない範囲です。これは、式 4-1-25 に示されています。この図では、0.5kHz までです。
この範囲で評価すると、式 4-1-18 の位相は、アナログと完全に一致しており、式 4-1-18 の方が優れています。
式 4-1-17 と式 4-1-18 との違いは、積分のやり方の違いですが、これは、図 4-1-33 のように説明されます。
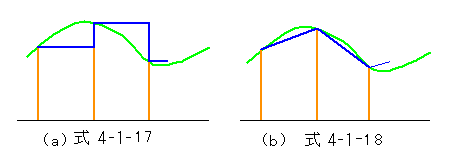
◆ この図からも、式 4-1-18 の方が、高い周波数でのアナログとの一致度が高いことが、了解されます。
◆ ステップ応答では、サンプリングとホールドとを 1 つにまとめて、サンプルアンドホールドとして取り扱いました。
周波数応答では、サンプリングの影響は、微分や積分の例で見てきたように、各要素の周波数応答に含まれています。しかし、ホールドは遅れを持っています。ホールドの遅れを考える必要があります。
また、中間出力や次回出力のときは、さらにその遅れも含めなければなりません。
◆ まずホールドによる遅れを調べて見ます。サンプルアンドホールドのサブサーキットSAHの、周波数応答を図 4-1-34 に示します。
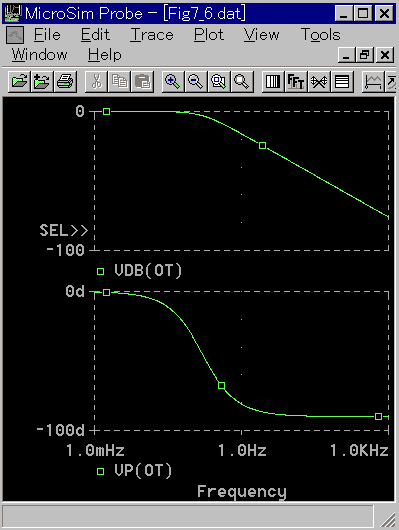
◆ この周波数応答波形は、明らかに 1 次遅れです。サンプルアンドホールドの特性が、1 次遅れと同じであるはずがありません。何かの間違いです。
PSPICE の AC 解析は、小信号入力です(2.1.6.(1-C)。系が線形であれば、入力信号の振幅が異なっても、出力波形は変わりません。
しかし非線形系では、信号の振幅によって応答が異なります。
サンプルアンドホールド回路は、スイッチを使用しています。スイッチは非線形要素です。AC 解析によって、スイッチとしての非線形特性が無視されて、一定値の抵抗と見なされてしまったのです。
このモデルで周波数応答を求めることはできません。
◆ ホールド単体は、下記のように考えることができます。
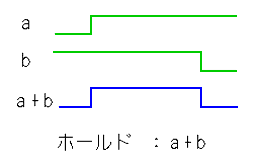
したがって、ステップ入力とむだ時間とから作ることができます。
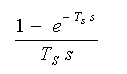・・・・ (4-1-26)
ここで TS は、ホールドタイム(=サンプリング周期)です。周波数応答を図 4.1.35 に示します。
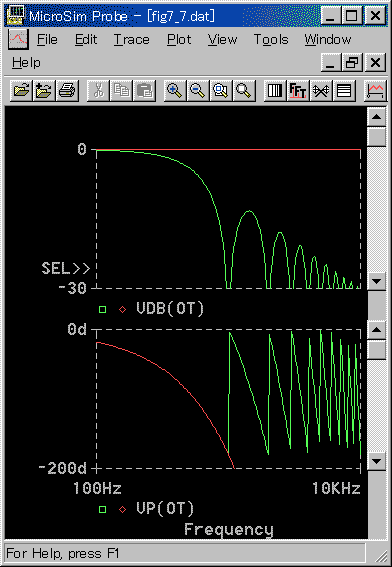
◆ 図の赤は、むだ時間 (= TS/2) です。ホールドは、位相に関しては、むだ時間と良く一致しています。ゲインは、減衰があります。周波数が高くない範囲で、これを無視すれば、ホールドは、むだ時間で近似することができます。
◆ 出力の遅れは、むだ時間と考えられます。同時出力のときゼロ、次回出力のとき、サンプリング周期に等しい値になります。
