


◆ AC 解析の例を試して見ます(リスト2-1-2)。回路ファイル名は tst02.cir です。これも、ディレクトリ cnt の sec21 に入っています。

◆ tst02.cir の概要を説明します。この回路ファイルには、回路(0) から回路(5) まで、6 個の回路が入っています。
まず、デバイスとコマンドを解説します。リスト 2-1-1 に出てきたものは解説を省略します。
◆ AC 解析の標準要素は、次の通りです。
.AC<DEC><点数><開始周波数><終了周波数>
( < > は、必須)
<DEC> : スイープの方法の指定です。DEC 以外の指定もありますが、自動制御では、通常、DEC を使用します。開始周波数から終了周波数までの間を、対数的にスイープします。
<点数> : 周波数 DECADE (10倍) 当たりの点数です。通常 20〜100 程度で差し支えありません。ただし、シャープなピークなどが存在する波形では、その部分を精密に表わすためには、点数を多く取る必要があります。
<開始周波数> : スイープを開始する周波数です。
<終了周波数> : スイープを終了する周波数です。
◆ 回路(0) の AC 解析を実行するための入力電圧 VC です。AC 解析では入力として AC 電圧を入力します。
AC 電圧源の一般的な書式は下記の通りです。
<V(名称)><+ノード><-ノード><AC<電圧振幅値>>
( < > は、必須)
一般の AC 電圧源では、AC 電圧を振幅値で記入します。
AC 解析の入力の場合には、振幅値に 1 を記入しなければなりません。
AC 解析では、実際の計算は、小信号入力として行われます。小信号入力とは、十分に小さい振幅の (理論上は無限小) の信号です。しかし、電圧振幅値を 1 に指定しないと、正しく表示されません。
◆ 回路(1) 〜回路(5) の入力電圧は、この VC ではなく、9 行目の電圧源 VC1 を使用しています。この例からも分かるように、PSPICE では、複数の入力による、複数の解析を、1 つの回路ファイルで、実行することができます。
◆ デバイス「C」はコンデンサ です。書式は抵抗「R」と同様です。
◆ デバイス「E」は、名前は電圧源となっていますが、このデバイスの用途の多くは、理想的な増幅器です。
現実に存在する増幅器 (オペアンプIC を使用した各種の増幅回路) は、かなり理想に近い特性を持っていますが、完全に理想的ではありません。これを現実特性と呼んでいます。
電子回路の解析では、通常は、この理想からずれた現実特性を持つものとしてオペアンプを取り扱う必要があります。この目的で、各種の市販オペアンプの現実特性のモデルが用意されています。
一方、増幅器が、理想特性を持っていると見なして、解析できる場合もあります。このときは、デバイス「E」を使用できます。ここでは、増幅器を、理想特性を持つとしています。
デバイス「E」は 4 個の端子を持つ 4 端子デバイスです。標準要素は、
<E(名称)><+出力ノード><-出力ノード><+制御ノード><-制御ノード><増幅度>
( < > は、必須)
です。各ノードの電圧を VOP (+出力ノード)、VON (-出力ノード)、VCP (+制御ノード)、VCN (-制御ノード)、増幅度を K
とすれば、この増幅器は次の式で表されます。
◆ トランジェント解析の例で、シミュレータの大体の様子が分かりましたから、今度はいろいろと試してみます。
回路ファイル tst02.cir をそのままシミュレーションするだけでなく、あれこれ書き換えて、実験を行ないます。
◆ 回路ファイル tst02.cir 内の 回路(0)〜回路(5)までの、6 個の回路は、互いに独立です。いずれも RC(抵抗/コンデンサ)による単純なフィルタ回路です。フィルタの周波数特性を、AC解析で求めます。
◆ 第 1 の実験として、グラウンドから浮いた回路は、エラーになる、ことを試してみましょう。tst02.cir の回路(0) の抵抗RD1 (リスト 2-1-2 の 7 行目) の行頭に * を挿入して、セーブしてください。
行頭が * の行はコメントですから、SPICE はこの行を無視します。すなわち、その行を消したことになります。
あるデバイスを、一時的に取り外した回路を、作りたいときに、その行を消去してしまうと、復活させるときに、その行を一から書き直さなければなりません。このようにコメントにしておけば、* を消すだけで、簡単に復活させることができます。
この、7 行目の行頭に * を入れた状態で、SPICE を実行します。すると、回路の三つのノード OT1、IN1、IN2 がフローティングであるという、下記のエラー・メッセージが出ます。
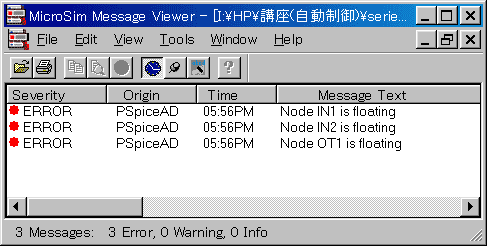
◆ 実際の回路は、グラウンド (大地) から浮いた回路でも動作します。しかし、SPICE では解析の演算は全てグラウンドを基準として計算します。このため、グラウンドから浮いた回路を解析することができません。
SPICE シミュレーションのための回路は、グラウンドを基準とした回路構成にする必要があります。
この回路は、グラウンドから浮いた回路がエラーになることを示すために作った回路です。通常の回路であれば、4行目と 6行目のノード IN2 のところは、グラウンド (ノード名 = 0) ですから、問題ありません。
◆ 実際の回路がグラウンドから浮いていて、この状態を解析したいこともあります。このようなときは、グラウンドから浮いた回路を作っておきます。その上で、この回路のように高抵抗値のダミー抵抗 RD1 でグラウンドに接続して、エラーになることを防ぎます。
実際の回路がグラウンドから浮いているといっても、その絶縁抵抗は無限大ではありません。ダミーの1GΩの抵抗は、一般の絶縁抵抗よりも、はるかに大きな値です。したがって、グラウンドから浮いた回路を、十分に模擬しています。
◆ この例のように、回路全体ではなく、部分的にグラウンドから浮いている所があっても、PSPICE ではエラーになります。コンデンサにはさまれた部分に、注意する必要があります(図 2-1-12)。
[注] PSPICEでは、コンデンサは、理想的なコンデンサですから、絶縁抵抗は無限大です。
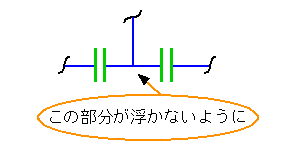
◆ 実際の回路が図のようになっている場合には、シミュレーションでは、ダミーの高抵抗でグラウンド等と接続する必要があります。
◆ ダミー抵抗 RD1 を復活させて (行頭に挿入した * を消す) PSPICE を正常に動作させ、PROBE の波形を描いて見ましょう。
最も一般的な周波数特性 の表現方法は、周波数 (常用対数) を横軸として、縦軸に振幅 (dB : デシベル) と位相 (°: 度) をプロットします。
この形式で周波数特性 (周波数応答) を表した図を、ボード線図 といいます。
.ACコマンドで DEC を指定していれば、周波数は常用対数で表示されます。
電圧出力を単に V(OT1) のように指定すると、対数でなく、リニアスケールで出力振幅を表示します。
信号の振幅を dB、位相を度で表示するためには、そのように指定する必要があります。振幅を dB で表示するには VDB(X)、位相を度で表示するには VP(X) を指定します。
VDB(OT1) の指定は次のように行ないます。まず、PROBE 画面において、Add Trace で V(OT1) を選択します。下欄の
Trace Expression で V(OT1) をVDB(OT1)に書き換えて、OKをクリックします。
同様にして、V(OT1) を、VP(OT1) に変えます。
◆ このようにして作成した PROBE画面を、図 2-1-13 に示します。なお、以降に示す画面は、PROBE画面の周囲をカットしたネットの部分のみの画面です。
[図 2-1-13] 回路(0) の AC解析 (RC回路)
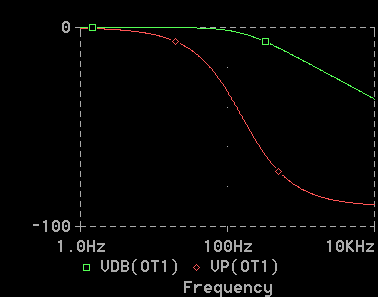
◆ 各ノードは、2 つ以上のデバイスに、接続されている必要があります。ノードは、デバイスとデバイスの接続点 (結節点)ですから、当然の話です。SPICE では、この条件を満たさないとエラーになります。
実際の回路でも、この条件を満たさないと、実用上意味のある回路にはなりません。しかし、このような部分があったとしても、実際の回路は、実用上意味の無い部分が動作しないだけで、全体としては、正常に動作します。
回路(1) において、(コメントを利用して) C11 を取り外すと、ノード OT11 の接続数は 1 になります。この状態で SPICE を実行してみましょう。エラーになり、エラーメッセージがでます。
◆ C11を復活させれば、この回路のフィルタ部分は回路(0) と同じです。PROBE画面に波形を表示すれば、回路(0)の波形(図 2-1-13) と同じグラフが得られます。
◆ この図では振幅と位相が同一の図にプロットされています。これを、複数の図に分けて表示することもできます。
まず、PROBE で、下になる図 (ここでは位相) を描きます。この図が表示されている状態で、PROBE画面で、「Plot」→「Add Plot」とクリックします。位相の図は下半分に移り、上半分にブランクの図が出ます。ここに振幅の図を描きます
(図 2-1-14)。
[図 2-1-14] 回路(1) の AC解析 (図を分ける)
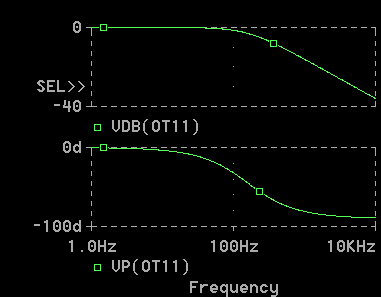
◆ なお、上の図の左側に「SEL>>」の表示が出ています。上下の図のうち、上の図が選択されていることを示すものです。反対側の図の中をクリックすることによって、選択を変更することができます。
選択された方の図は、自由に編集することができます。図の編集を行うためには、まず、編集する方の図を、選択する必要が、あります。
◆ 回路(1) に対して、抵抗とコンデンサの位置を逆にした回路です。
この回路(2) のところには、AC 解析のための AC 電圧入力が書いてありません。
しかし、回路(2) の入力点 IN11 は回路(1) の入力点 IN11 と同じノードですから、回路(1) のところに書いてあるAC 電圧源 VC1 を共用しています。回路(3) 以降についても、同様に回路(1) の AC 電圧源 VC1 を共用しています。
[注] 回路(0) は独立の AC電圧源を使用しています。回路(0) はグランドから浮いていて、回路(1)〜(5) とは、つながっていませんから、当然、共用することはできません。
◆ 回路(1) と同様にして、PROBE で波形を表示します (図 2-1-15)。ここでは、回路(1) の特性と比較するために回路(1)も、同時に、表示してあります。図 2-1-15 の上側が振幅、下側が位相です。そして、OT21 が回路(2) の出力信号、OT11 が回路(1) の出力信号です。
[図 2-1-15] 回路(2) の AC解析 (CR回路)
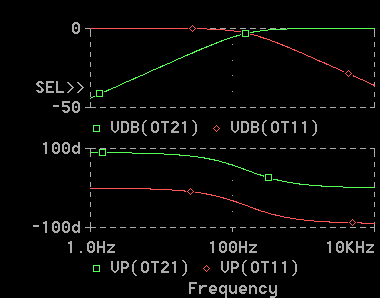
◆ 回路(1) (RC回路) の周波数特性に対して、回路(2) (CR回路) の周波数特性は、振幅はちょうど左右対称に、なっていることが、分かります。位相は垂直方向に、平行移動しています。
回路(1) のように、周波数が低い領域はそのまま通し、周波数の高い領域を減衰させる特性を、もつ回路をローパス・フィルタ といいます。回路(2)のように、それと逆の特性を持つフィルタを、ハイパス・フィルタ と呼んでいます。
また、抵抗 R と、コンデンサ C、各 1 個で構成され、図 2-1-15 に示すような、周波数特性を持つフィルタを、1次フィルタ といいます。
◆ 今度は、RC を 2 段重ねにした回路です。この回路のように、ある回路の出力が次の回路の入力になっている回路構成を、カスケード接続 と言います。
SPICE を実行し、PROBE 画面を作ります。まず、振幅について示します。最終出力 V(OT33) のほかに、中間出力
V(OT31) および、比較のための V(OT1) も表示させます。
そのままでは、グラフが込み入っていて、画面が見やすくありません。PROBE は、画面の表示スケール、を変換することができます。画面を拡大してみましょう。
X 軸のスケールを変換するには、「Plot」→「X Axis Setting」を、クリックします。
◆ ここで、「Data Range」が「Auto
Range」になっています。「User Defined」をクリックして、レンジを記入し、「OK」をクリックします。
同様にして、Y 軸も変更できます。その結果が、図 2-1-16 です。
[図 2-1-16] 回路(3) の AC解析、振幅 (RC 2段)
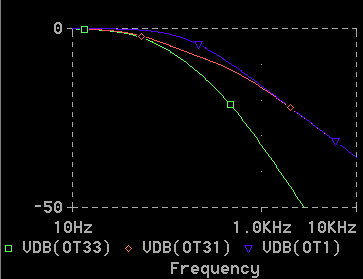
◆ RC 1 段の波形(VDB(OT1))に対して、RC 2 段(VDB(OT33))の方が、フィルタ特性が、シャープになっていることが、分かります。RC 1 段のときは、高周波領域の振幅(dB) 減衰量は 20dB/DEC です (DEC は周波数 10倍を表す)。RC 2 段のときの中間点も、同じです。
これに対して、RC 2 段の高周波領域の減衰量は、40dB/DEC になっています。
なお、RC 2段の中間点 V(OT31) は、RC 1段の V(OT1) よりも、中間の周波数領域で、減衰が、ゆるやかになっています。これは、カスケード接続によって、後段の回路が、前段に、影響を与えているからです。
◆ 次に、位相を表示してみましょう (図 2-1-17)。RC 1 段(VP(OT1))のときは、高周波領域の、位相遅れは-90゜です。RC 2段(VP(OT33))では、-180゜となります。
[図 2-1-17] 回路(3) の AC解析、位相 (RC 2段)
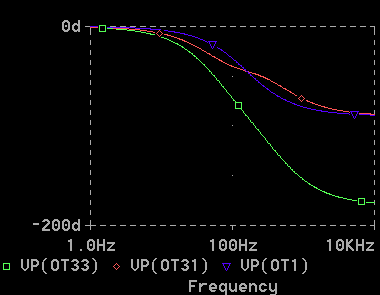
◆ RC 2 段の場合、中間の周波数領域で特性がゆるやかになることは(VP(OT31))、振幅のときと同様です。
◆ 回路(4) は RC 2 段ですが、1 段目と 2 段目の間に増幅器 E41 が入っています。この増幅器の増幅率は 1 ですから、増幅器の、入力と出力の波形には、変化がありません。
このような増幅率 1 の増幅器をバッファ と呼んでいます。
バッファを挿入することによって、バッファ後段の回路が、バッファ前段の回路に、影響を与えないように、なります。回路(4) と比較のために、回路(3) も、表示する画面を作ります (図 2-1-18)。
ここでは、振幅の画面だけを示しますが、位相の画面も、各自作ってみてください。
[図 2-1-18] 回路(4) の AC解析、振幅 (バッファあり)
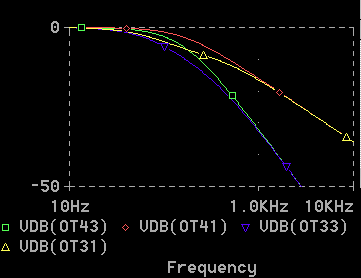
◆ バッファを挿入した、回路(4) では、後段の回路が、前段の回路に、影響しないので、中間の周波数領域の特性が、改善され、よりシャープなフィルタに、なっていることが分かります。
◆ 回路(5) は RC 3 段です (図 2-1-19 〜図 2-1-20)。各段の間にはバッファが入っています。
[図 2-1-19] 回路(5) の AC解析、振幅 (RC 3段)
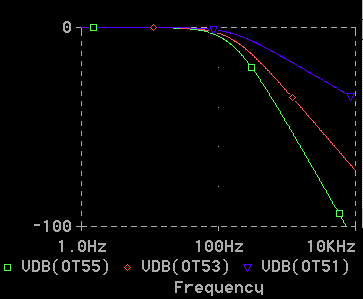
[図 2-1-20] 回路(5) の AC解析、位相 (RC 3段)
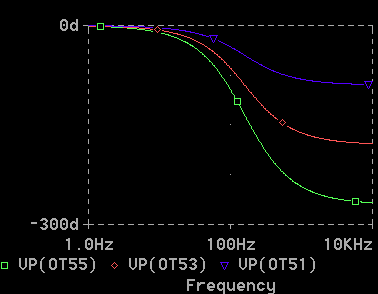
◆ 高周波領域において、1 段、2 段、3 段の、振幅の減衰量は、それぞれ、-20dB/DEC、-40dB/DEC、-60dB/DEC に、なっています。位相の遅れは、それぞれ -90°、-180°、-270°です。
◆ RC を n 段カスケード接続した、フィルタを、n 次フィルタ と呼んでいます。上記の例から推定されるように、n 次フィルタは、下記の性質を、持っています。
高周波領域における減衰量は n×(-20) dB/DEC である。
高周波領域における位相遅れは、n×90°である。
◆ 以上、各種のフィルタを眺めてきました。いずれも、抵抗 R とコンデンサ C の組み合わせが基本要素になっています。
この各々の要素において、抵抗値 R と容量値 C の積をフィルタの時定数 と呼んでいます。すなわち、時定数 T は、
T = R C
です。このテスト回路-2 では、抵抗はすべて 1kΩ、コンデンサはすべて 1 μF ですから、時定数も、すべて 1 kΩ × 1μF = 1ms です。
時定数を変えると、フィルタの周波数特性は周波数軸に沿って水平に移動します。移動する周波数は、時定数に反比例します。
◆ たとえば、回路(1) において抵抗を 10 倍にしてみましょう。それによって、時定数は 10 倍 (10ms) になります。周波数特性は振幅も位相も 1 DEC 分だけ左にずれます (図 2-1-21)。すなわち、周波数 1/10 に移動したことになります。
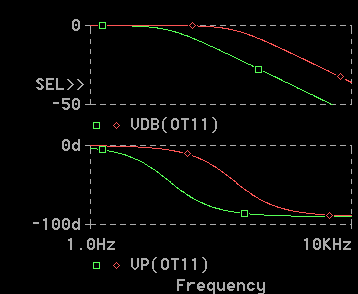
◆ この図には、比較のために、元の波形を入れてあります。図 2-1-21 で、□ (緑) が時定数 10ms の波形、◇ (赤)が元の時定数 1ms の波形です。
[注] 複数の波形を重ね合わせて表示する方法は、ここでは説明しません。結果だけを示します。
逆に、時定数が等しければ、抵抗と容量の値が異なっていても、周波数特性は、同じになります。たとえば、回路(1) で抵抗を
10倍 (10kΩ) 、容量を 1/10 (0.1μF) にすると、 時定数は元のまま (1ms) です。波形も元のままです(各自試みてください)。
なお、2次以上のフィルタの場合は、周波数特性の波形を変えずに、周波数軸に、平行移動させるためには、すべての要素の時定数を、同じ比率で、変化させる必要があります。