


◆ 実際のケーブルと全く同じ周波数特性のモデルを作り上げれば、間違いは無いはずです。代表的なケーブルである、市内ケーブルと同軸ケーブルの周波数特性は、図.5 と図.9 に示しました。この特性を、そのままシミュレーションモデルにしてしまおうという考え方です。
◆ PSPICE では、要素の特性を周波数テーブル で表すことができますから、これを使用して、上記の図をそのままモデル化します。デバイスは、E を使用します。書式は、
E<名称><+ノード><-ノード>FREQ {<式>} = <<周波数値>,<振幅値>,<位相値>>*
です。* は、必要数繰り返すことを表します。データは、周波数が小さい方から大きい方に順に並べる必要があります。テーブルでは、与えたデータの間は内挿されます。与えたデータの最小値以下は最小値、最大値以上は最大値が外挿されます。
◆ この方式の欠点は、線種、線径と長さ毎にそれぞれテーブルを用意しなければならない点です。
PSPICE では、一般論として、値を直接記述しないで記号を使用し、別のところでその記号に対して数値を与えて、演算を行わせることができます。これをパラメータ と呼びます。たとえは、回路ファイルの中で、抵抗値を文字 rs として記述しておき、別のところで、rs = 100 と指定することができます。しかもこのパラメータには、式を使用することができます。
◆ したがって例えば、ケーブル長さを、LEN で表わし、単位長さ当たりの減衰量を 15 とすれば、任意の長さの減衰量は、(15 * LEN) となります。このようにパラメータを使用して周波数テーブルを作ることができるなら、線種と線径毎にモデルを作ればよく、長さはパラメータとして任意長さを指定できます。
[注] コンピュータのプログラムと同様に、PSICE における演算でも、乗算記号は * です。
◆ ところが残念なことに、PSPICE(8) では、周波数テーブルでは、パラメータを使用することができません。したがって、長さ毎に異なるモデルを作る必要があるのです。このようにして作った周波数テーブルの例を、リスト 4.1 に示します。
[注] 周波数テーブルを使用することができ、かつ、その中でパラメータを利用できる SPICE があるかどうかは知りませんが、もしあるなら、これを利用してモデルを作ってください。
[リスト 4.1] 周波数テーブルによる伝送路の周波数特性の例
* CPEV 0.65D 100m UP TP 300MEG
E1 out 0 FREQ {V(in)} = (10,0,0)(100,-0.04,-0.03)
+ (1k,-0.11,-0.18)(3k,-0.165,-0.4)(10K,-0.25,-0.8)
+ (30K,-0.38,-2)(100K,-0.62,-3.9)(300K,-1.02,-7.7)
+ (400K,-1.22,-9.2)(600K,-1.57,-12)(1MEG,-2.15,-16)
+ (1.5MEG,-2.76,-21)(2MEG,-3.30,-25)(3MEG,-4.2,-32)
+ (4MEG,-5.0,-38)(6MEG,-6.5,-49)(.01G,-8.9,-67)
+ (.015G,-11.4,-86)(.02G,-13.6,-102)(.03G,-17.5,-131)
+ (.04G,-20.9,-157)(.06G,-26.9,-202)(.1G,-36.8,-276)
+ (.15G,-47.3,-355)(.2G,-56.5,-424)(.3G,-72,-544)
◆ このリスト(以降も同様)では、リストを見やすくするために、各行の先頭を空けてありますが、実際には行頭から開始しなければなりません。
最初の行はコメントです。コメント行は、行頭に * をつけます。
2 行目からが、周波数テーブルのデバイス E です。各デバイスやコメントは、1 行に書く必要があります。ただし、この 1 行とは、書式上の 1 行であって、リターン記号を書かずに連続して書けば 1 行とみなされます。
◆ ただし、これでは見難いので、リストに示したように、見やすいところで区切ってリターンを入れ、次の行頭に + を入れます。このようにすれば、1 行に連続しているとみなされます。また、リストに示したように、+ の後の実際の書き始めまでの間に、任意数のスペースやタブを入れて差し支えありません。したがって、E1 から最後までが 1 行であり、1 デバイスです。
◆ リストの内部は、書式に示したように、周波数値、振幅値、位相値を組にして、繋げて書きます。この組の間に、)( を入れてありますが、これは見やすくするためで、単にスペースでも差し支えありません。
[注] PSPICE の回路ファイル(*.cir)では、大文字と小文字とは区別されません。どちらを書いても同じです。このため紛らわしいのが、補助単位の「ミリ」と「メガ」です。回路ファイルの中では、m も M も、ともにミリと解釈されます。メガの場合には、MEG または meg と書かなければなりません。
◆ このテーブルは、伝送路の減衰量の周波数特性をよく表わしています。しかし、そのままでは実用になりません。次に示す、直流抵抗による補正が必要です。
このモデルは、減衰量は正しく表わされていますが、位相は伝送路の遅れを表わしていません。位相は、実際の遅れよりも十分に小さい適当な値を入れてあります。伝送路は、単に遅れだけでなく反射があります。この反射の現象を含んだモデルには、デバイス TRANSMISSION LINE を組み合わせて使用する必要があります。したがって、この周波数特性モデルには、位相遅れを組み込む必要はありません。
◆ しかし、位相遅れをゼロにしたモデルでは、出力が異常な波形になります。これを防ぐために、実際の遅れに対して無視できる程度の位相遅れを組み込んだモデルになっています。
ただし、このやりか方で作った位相遅れを使用したモデルは、次に示す、直流抵抗による補正を行ったモデルでないと、実際の伝送路の特性と大きく異なってしまいます。
◆ リストに示したモデルの周波数特性を、図.14 に示します。
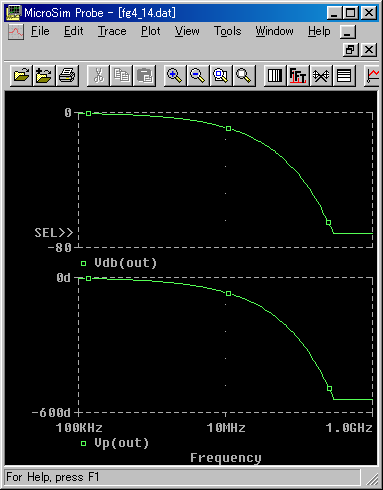
◆ 図から分かるように、周波数は 300MHz までをカバーしています。PSPICE では、周波数特性の形で表わされているモデルの、トランジェント解析を求めることができます。パルス波形の応答を調べるときは、パルス幅の 10 倍以上の周波数までの周波数帯域が必要です。
[注]
最近は、より高周波の使用が多くなっています。このため、より高い周波数をカバーするテーブルが必要になります。図.5 は、高い周波数をカバーしていません。周波数テーブルでは、図.5 を大幅に外挿しています。CPEV の場合には、外挿によってテーブルの周波数を延ばしても、差し支えありません。
一般論としては、高い周波数になるほど、損失の要因が増えますから、直線外挿よりも減衰量が大きくなります。この損失の増加は、ほとんどがケーブルの絶縁体の材質に起因します。CPEV の絶縁体は、ポリエチレンです。ポリエチレンでは、作成している周波数テーブルの周波数範囲では、直線外挿して差し支えありません。
◆ この図.14 の回路ファイル fg4_14.cir のリストを リスト 4.2に示します。
fg4_14 frequency response cpev 0.65 D 100m
.ac dec 40 100k 1g ; AC 解析のコマンド
vac in 0 ac 1 ; AC 解析用の電圧源
xline in out cpev60s ; サブサーキットのコール
.lib "../dtran.lib" ; ライブラリファイルのコール
.probe ; 終了処理(probe のコール)
.end ; 終了処理(終了コマンド)
◆ これ以降、読者が自分でシミュレションを行うことができる回路ファイルは、ファイルをダウンロードすることができます。この場合、分かりやすいように、回路ファイルのファイル名称は、図番号と同じにします。ただし、同じファイル名称ができないように、回路ファイルには、章番号を付加します。この例では、関連する図が、図.14 なので、回路ファイルは、fg4_14.cir です。
[注1]
ダウンロードの方法は、自動制御 2.1.3.(3) にあります。なお、この講座では、ダウンロードしたデータは圧縮されていませんから、そのまま使用できます。
この講座で使用する回路ファイルは、ほとんどがライブラリを使用しています。使用する回路ファイルと、ライブラリの相対位置は、自動制御 2.1.3.(3-A) に示したようになっている必要があります。
[注2]
波形(probe)図上部に示されているファイル名は、*.dat です。PSPICE では、SPICE の演算を行うと、回路ファイルが置かれているフォルダに、同一名称で拡張子が異なる幾つかのファイルを作ります。
*.dat ファイルは、*.cir を演算した結果のデータが収容されているファイルです。
probe は、この *.dat ファイルの内容を作図したものです。
◆ 回路ファイルの先頭行は、(指定無しに)必ずコマンドです。この先頭行のコマンドは、波形(probe)画面をプリントしたとき、プリントの表題としてプリントされます。このとき、日本文字だと文字化けします。したがって、この行だけは、英数字で書いた方が良いでしょう。
◆ 行の先頭に * があるときはその行が、行の途中に ; があると、その行の ; 以降はコメントになります。これも、PSPICE のプログラムで読むと文字化けします。しかし、回路ファイル(*.cir)を読み書きするのは、通常テキストエディタです。テキストエディタが日本語をサポートしていれば良いわけです。PSPICE の *.cir ファイル以外のファイルで、コメントの部分が文字化けしても、ほとんど実害はありません。日本文字を使用しても良いでしょう。
◆ このリストは、コメントを十分に入れてあります。コメントを多く入れる方が、分かりやすくなります。
[注] この cir ファイルの内容は、*.out ファイル(PSPICE を動作さたときに、PSPICEが自動的に作るファイル)上にも現れます。しかし、*.out を読む必要がるときでも、コメントを読む必要は、ほとんどありません。
◆ 伝送路の特性で、もう 1 つ考慮しなければならないのは、直流抵抗 です。伝送路の特性インピーダンスは、交流の性質です。そして、周波数が低くなれば、非常に小さな値となります。しかし実際には、伝送路の直流抵抗のために電圧降下が起こり、電流値は制限されます。
◆ この現象(図.15)をモデルに組み込むことが必要です。

◆ この図.5 のモデルの形は極めて単純なのですが、実際に定量的なモデルを作ることは、かなり大きな手間が掛かります。このモデルの場合、伝送路の周波数特性の位相特性をうまく決めなければ、伝送路のトランジェント解析波形を、実際の伝送路の波形と合わせることができません。位相特性がトランジェント波形に大きく影響するのです。しかも、この位相合わせは、うまい目安が無くて、トライアルになります。
◆ この問題を避けるために、多少乱暴なやり方ですが、図.16 に示すように、周波数テーブル自体を補正することによって、直流抵抗の影響を、モデルに組み込んでいます。
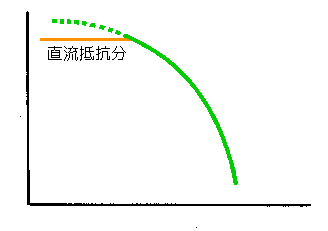
◆ 抵抗による減衰は、周波数特性を持ちませんから、ボード線図のゲインは、水平な直線になります。したがって、図に示すように、この水平な直線によって頭打ちにします。このとき、同じ伝送路でも、信号源インピーダンスや負荷インピーダンスによって、電流値が異なりますから、減衰量も変化します。
◆ しかしこれをモデルに組み込むことは、実用性がありません。そこで、適正に終端した条件、すなわちケーブルの特性インピーダンスと同じ値の抵抗で終端したときの減衰量に統一します。このようにすれば、伝送路の長さが決まれば、直流抵抗による減衰量は一定になります。実用上は、ほとんどこのモデルで十分です。これを使用することにします。
◆ この補正方式は、都合が良いことに、位相遅れの大きさを変えても、特性への影響が、あまり無いことです。このため、テーブルの位相遅れは、周波数によって滑らかに変化させれば良く、その大きさは、適当で差し支えありません。
◆ この講座で使用する周波数テーブルは、この方式で作成してあります。
◆ 以上で、周波数テーブルによる伝送路のモデルを作ることができます。しかし、このままでは、同じ線種、同じ線径のケーブルに対して、長さが異なる多数のモデルを用意しなければなりません。
これは、作るのにも、使うのにも共に不便です。そこで、使いやすいように、ケーブル長さをパラメータとして指定できるサブサーキットを作りました(図.17)。
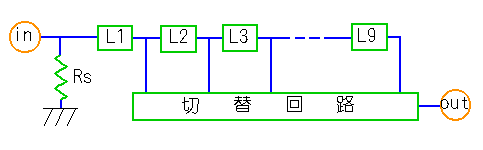
◆ この図は、サブサーキットの概念を示すものです。サブサーキットの実際の構成とは異なります。
in は入力、out は出力です。最初の Rs は、伝送路の等価入力インピーダンスです。したがって、in の電圧は、伝送路の信号源の等価出力インピーダンスと Rs とによって分圧されます。この Rs は、実際の伝送路の特性インピーダンスと同じに働きます。
◆ 信号は、L1、L2、L3 と直列に進みます。これらは、リスト 4.1 に示したような周波数テーブル(直流抵抗による頭打ちを入れたもの)による伝送路の周波数特性モデルです。周波数特性モデルでは、信号がモデルを直列に進むと、伝送路の長さが加算されます。
実際のサブサーキット マルチライン mult は、リスト 4.3 です。
.subckt mult in out params: z0=100,rdc=1u,lg1=0,lg2=0,lg3=0,
+ lg4=0,lg5=0,lg6=0,lg7=0,lg8=0,lg9=0
* 入力特性インピーダンス
r1 in 0 {z0}
* ライン
xlin1 in 1 mul
xlin2 1 2 mul
xlin3 2 3 mul
xlin4 3 4 mul
xlin5 4 5 mul
xlin6 5 6 mul
xlin7 6 7 mul
xlin8 7 8 mul
xlin9 8 9 mul
* ライン切替え
e1 10 0 value= {lg1*v(1)+lg2*v(2)+lg3*v(3)+lg4*v(4)+lg5*v(5)
+ +lg6*v(6)+lg7*v(7)+lg8*v(8)+lg9*v(9)}
* 直流抵抗
r2 10 out {rdc*(lg1+2*lg2+3*lg3+4*lg4+5*lg5+6*lg6+7*lg7+8*lg8+9*lg9)}
.ends
◆ このサブサーキットは、任意の伝送路モデルと組み合わせて、その長さを、1〜9倍に、9 段階に変化させるサブサーキットです。組み合わせる伝送路モデルの長さを、たとえば 10m のものと、4m のものとを作ると、
10、20、30、40、50、60、70、80、90m
4、8、12、16、20、24、28、32、36m
となりますから、
10、12、16、20、24、28、30、32、36、40、50、60、70、80、90
のものを作ることができ、実用上十分な間隔で長さが求まります。
◆ このサブサーキットを使用することを前提として、この講座のライブラリでは、伝送路長さが 1×10n と 4×10n の 2 系列の長さの伝送路モデルを用意してあります。伝送路モデルの名称の付け方については、ライブラリ drtran.lib を参照してください。
◆ このサブサーキット mult は、伝送路モデルを指定して呼び出します。この呼び出しは、回路ファイルの中で、サブサーキットコールを使用します。すなわち、
.subckt mul in out
xlin in out 伝送路の名称(たとえば cpev601)
.ends
を使用します。
◆ パラメータ z0 は、図.15 に示した Rs の値です。伝送路の特性インピーダンスの値を使用します。たとえば、cpev であれば、100 です。デフォルトは 100 になっています。
パラメータ rdc は、使用する伝送路モデルにおける伝送路の直流抵抗の値です。講座で使用する伝送路モデルには、減衰量の頭打ちの形で組み込まれていますから、これを使用する必要性はありません。したがってデフォルトでは ≒0 になっています(デバイス R では値をゼロにすることはできません)。
◆ lg1 から lg9 までが、接続数を指定するパラメータです。デフォルトは全てゼロです。使用するとき、親回路の X デバイスのパラメータ指定で、指定したい値のものを 1 にします。たとえば、5 段にしたいときは、lg5=1 とします。
◆ 伝送路の遅れと反射の現象とを取り入れて、伝送路の総合特性を表わしたのが、サブサーキット line です。このモデルのブロック図を図.18 に示します。
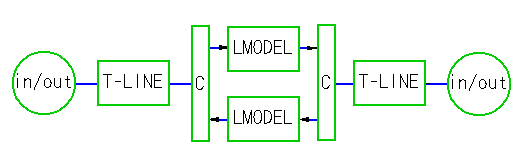
◆ 伝送路は、当然双方向性です。減衰量の周波数特性を表わす伝送路モデルには、方向性があります。これを双方向に変えます。双方向性を持たせるための制御回路が C です。
遅れと反射を持たせるためのデバイス TRANSMISSION LINE (図では T-LINE)は、双方化された LMODEL の両側に、それぞれ 1/2 の大きさで設けます。単純なモデルですが、実際の伝送路の特性を良く表わしています。
サブサーキット line のリストを リスト 4.4 に、その使用例を図.19 に示します。
.SUBCKT LINE V1 V2 PARAMS: R0=100 LEN=100 R1=1MEG R2=1MEG
xlin1 O1 LI1 LIN
xlin2 LO2 LI2 LIN
T1 2 0 V1 0 Z0={R0} TD={2.5N*LEN}
R2 2 0 {3*R0}
R3 2 4 {0.75*R0}
R4 3 0 {0.75*R0}
R5 3 4 {0.75*R0}
R6 4 5 {1.5*R0}
R7 LI2 0 {R1}
E1 LO1 0 2 3 8
E2 5 0 LI2 0 1
E11 LO2 0 12 13 8
E12 15 0 LI1 0 1
T11 12 0 V2 0 Z0={R0} TD={2.5N*LEN}
R12 12 0 {3*R0}
R13 12 14 {0.75*R0}
R14 13 0 {0.75*R0}
R15 13 14 {0.75*R0}
R16 14 15 {1.5*R0}
R17 LI1 0 {R2}
.ENDS
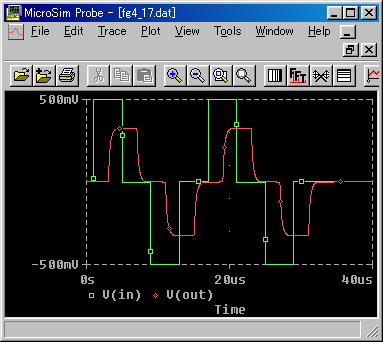
◆ この例は、適正に終端されていますから、反射はありません。伝送路の周波数特性による波形歪みと遅れだけが現れています。
ここに示した波形は、バイポーラ符号 と呼ばれるものです。具体的な解説は 第 6 章で行いますが、実際の伝送に多く使用されている符号です。
◆ 回路ファイルをリスト 4.5 に示します。
[リスト 4.5] サブサーキット line の使用例の回路ファイル
fg4_17 transient resoanse example for subckt line .TRAN 20N 40U 0 20n uic ; トランジェント解析の指定 VP1 1 0 PWL(0,0)(1U,0)(1.01U,1)(5U,1)(5.01U,0)(9U,0) +(9.01U,-1)(13U,-1)(13.01U,0)(17U,0)(17.01U,1)(21U,1)(21.01U,0)(25U,0) +(25.01U,-1)(29U,-1)(29.01U,0) ; 信号波形の指定 rs 1 in 100 xline in out line params: len=400 rl out 0 100 .subckt lin in out xln in out mult params: lg4=1 .ends .subckt mul in out xmult in ou cpev601 .ends .lib "..\dtranl.lib" .probe .end
◆ この fg4_19.cir は、サブサーキット line と、サブサーキット mult の両方を使用している例です。このようにすれば、任意長さの双方向性伝送路をシミュレートすることができます。
[注]
この fg4_19.cir を実行すると、警告(warning)のメッセージが、別ウィンドウ(MicroSim Message Viewer)で表示されます。この MicroSim Message Viewer は、警告のほか、エラーがあって、演算が不可能だったときにも、エラーメッセージが出されます(自動制御 2.2.8. コラム 2-2-4 参照)。
しかし、警告が出ても、出力波形は正常と思われるときもあります。この例も、警告は出ていますが、信用できる波形と考えられます。逆に、警告が出なくても、明らかに波形が正常とは考えられないこともあります。