◆ この講座では、具体的な制御例として、DC モータの制御を取り上げます。さきに述べたように、最近では、DC モータは、多くは使われていません。
しかし、DC モータの制御が基本です。しかも簡単で分かり易いので、この講座の実例として手頃です。
まず、DC モータのシミュレーション・モデルを作ります。
◆ DC モータは、電気的にはコイルです。コイルはインダクタンス L と抵抗 R で近似されます。電圧を E、電流を I とすれば、図 6-1-18 のようになります。これは、1 次遅れです(3.1.3.(1))。
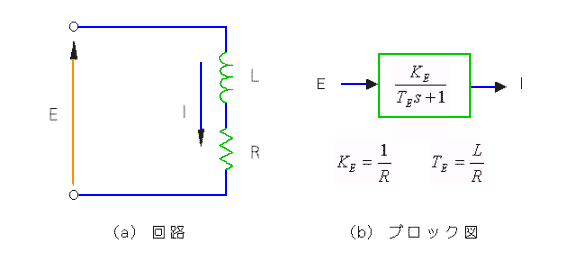
◆ この時定数 TE を DC モータの電気的時定数 といい、DC モータの基本定数です。
◆ DC モータを機械的に眺めると、質量 をM の物体に、力 F が加わり、この力によって物体は、加速度 α で運動します。
物体の速度 Ve は、加速度 α を積分( 1/s )することによって求まります。同様に位置 X は、速度 Ve を積分したものです。
ここで、力のバランスを考えると、上記の加速度 α による M・α のほかに、摩擦による減衰係数 Kv によって、速度 Ve に比例して発生する Kv・Ve があります。
また、外乱として τ を考えます。モータに加わる外乱は、力とは別の形を取ることも多いのですが、ここでは力の形で代表させました。したがって、
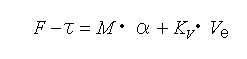・・・・ (6-1-2)
が成立します。
◆ これをブロック図で表わすと図 6-1-19 になります。
◆ モータのモデルでは、加速度を必要とすることは少ないので、これを消去してまとめます(3.1.1.(6-C) 図 3-1-11 (17))。これを図 6-1-20 に示します。
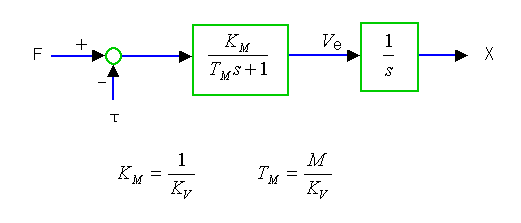
◆ すなわち、速度を出力にとれば、1 次遅れになります。この時定数 TM も、モータの基本定数です。
ただし、一般に機械的時定数と呼ばれている定数は、これとは別のものです((2-B)参照)。一般には名前を付けていませんが、この講座では、この定数 TM のことを、メカ時定数 と呼ぶことにします。
なお、上記の特性は、力 F や位置 X 等を使用しています。モータは回転体ですから、本来は力 F ではなくトルク Mt を、質量 M ではなく慣性モーメント J 等を使用する必要があります。
このときは、下記のように置き換えれば、式の形は同じです。
位置 X → 回転角度 θ
速度 Ve → 角速度 ω
質量 M → 慣性モーメント J
力 F → トルク Mt
◆ モータを、アクチュエータとして使用するときは、モータの回転運動を、直線運動に変換することも多いと思われます。
この講座では、アクチュエータを考えることが多いので、直線運動に変換した後の、力 F や位置 X を使用しました。
◆ モータでは、式 6-1-1 に示したように、電流に比例して力が発生します。したがって、これによって電気的特性と機械的特性とを結合して、総合特性を求めることができます。
ただし、これだけでは不充分です。さらにモータの発電機としての作用を付け加えることが必要です。
DC モータの構造は直流発電機と同じですから、発電機としても働きます。
回転によって、起電力 EG が発生します。モータに外部から加えた電圧からこの起電力を引いたものが,モータに加わります。
これらを総合した、モータの総合特性 を、図 6-1-21 に示します。
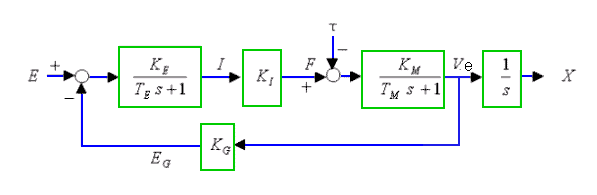
◆ 図から分かるように、モータ自体の特性がフィードバックを持って持っています。
ここで、モータの電流 I〜トルク F の関係 KI をトルク定数 、回転速度 Ve〜起電力 EG の関係 KG を逆起電力定数 といいます。
トルク定数の単位は N・m/A、逆起電力定数の単位は V・s/radですが、実は、この2つは次元が等しく、値も同じです。
◆ 図 6-1-21 に示した、モータ単体の総合特性を、サブサーキットにしてあります。
ただし、図のままだと、減衰係数をゼロにすることができません。実際のモータでは、減衰係数をゼロで近似できる場合が多いのです(6.1.4.(2-A)参照)。減衰係数をゼロにすることができるように、モデルを変形し、PSPICE 用に変数名を変えてあります(図 6-1-22)。
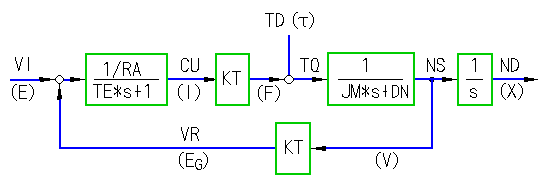
◆ 変数等を、表 6-1-1 に示します。
| 記号 | 名称 | 単位 | 種別 |
|---|---|---|---|
| VI | 入力電圧 | V | 入力変数 |
| TD | トルク(外乱) | N・m | 入力変数 |
| CU | 電流 | A | 出力変数 |
| NS | 回転速度 | rad/s | 出力変数 |
| ND | 回転角度 | rad | 出力変数 |
| TQ | トルク(電流変換) | N・m | 内部変数 |
| VR | 逆起電力 | V | 内部変数 |
| RA | アマチュア抵抗 | Ω | パラメータ |
| TE | 電気的時定数 | s | パラメータ |
| KT | トルク定数 | N・m/A | パラメータ |
| - | (逆起電力定数) | V・s/rad | パラメータ |
| JM | 慣性モーメント | kg・m・m | パラメータ |
| DN | 減衰定数 | N・m・s/rad | パラメータ |
◆ 入力変数は、サブサーキットの入力です。
出力変数は、サブサーキットの出力です。
内部変数は、サブサーキット内部で使用されている変数です。
パラメータは、サブサーキットで使用されている定数で、値をサブサーキットのパラメータとして指定します。このパラメータのデフォルトは、6.1.5.(1-A-a)の表 6-1-2 に示したモータ単体です。
[注]
内部変数は、サブサーキットの内部で使用されている変数です。サブサーキットの内部変数は、シミュレーションを実行したとき、PROBEで表示することができます。
自分でシミュレーションを行っている読者は、試してみてください。
PROBEの TRACE ADD で示される変数で、電圧であれば V((サブサーキット・デバイス名).(サブサーキット内変数名))と表示されます。
たとえば、後に示す図 10-2の FIG10_2.CIR において、モータの内部変数「逆起電力」であれば、V(XMOT.VR) です。
◆ サブサーキット MOTOR の書式は、
* 電流 速度 角度 電圧 外乱T 抵抗 電気定 トルク定 慣性モ 減衰定 .SUBCKT MOTOR CU NS ND VI TD PARAMS: RA=2.4 TE=0.9M KT=55M JM=8.3U DN=0
です。デフォルトは、講座で使用しているモータの定数です。
◆ 制御対象のモデルは、少なくとも3次遅れ以上、または無駄時間を含む必要があると、3.2.3.(1) で、説明しました。
モータのモデル(速度出力)は、2次遅れ系です。上記の条件を満たしていません。
モータ自体についても、さらに詳細な特性を考えたモデルを作れば、3 次以上の遅れになります。
また実際には、システムを構成するモータ以外の要素(たとえば電源装置)の特性が、効いてきます。これらの特性を加えれば、3 次以上のモデルになります。
なお、3.2.3.(1) で述べたことは、制御系を解析するために十分なモデルの条件です。たとえは限界感度法を適用するためには、3 次モデルが必要です。
しかし、シミュレーションによる制御系の解析を行う場合には、実際とのずれは大きくなりますが、多くは、2 次モデルで間に合います。
◆ DC モータでは、2 次遅れ(3.1.3.(2))近似モデルが、多く使用されてきました。
上記の総合特性や、それに基づいたサブサーキットは、ループを持っていますが、2 次遅れです(ループを開いて計算して見てください)。
この意味では、すでに2 次遅れです。以下に示すモデルを、あえて 2 次遅れ近似モデルと呼ぶのは、2 つの意味があります。
第 1 は、図 6-1-21 の基本モデルの中で、無視できるものを、無視したモデルだからです。すなわち減衰を無視します。
DC モータは、ブラシがあるので、減衰は無視できないように思われます。しかし通電時には、電流が潤滑の役割を果すので、減衰を無視できます。
◆ 第2は、ループを解いて計算したモデルを、使用するということです。
2 次遅れ近似モデル を、図 6-1-23 に示します。
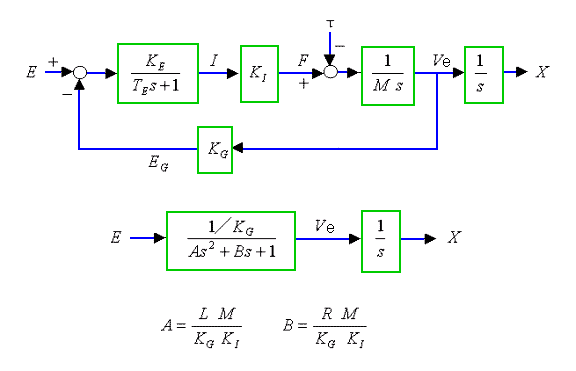
◆ 図の上側が、無視できるものを省略したモデル、下側が、ループを開いた 2 次遅れ近似モデルです。
シミュレーションを容易に利用できなかった時代には、式の形とそのパラメータの値を見ただけで、その応答の目安を付けることができることが重要でした。ループ形のモデルは、この意味で不合格でした。
制御対象が 2 次遅れのとき、これを P 動作で制御すると、制御系全体も 2 次遅れです。2 次遅れは、パラメータの値で、応答波形を推定することができます(3.1.3.(2-B))。
[注] DC モータが 2 次遅れと見なせるのは、出力が回転速度のときです。出力が回転角度のときは、それに積分が加わります。
◆ ただし、ループを解いて計算した結果として、電流 I と力 F とが失われます。シミュレーション用のモデルとしては、電流 I と力 F とが、モデル上に表現されている方が汎用性があります。
とくに電流は、制御に利用されることも多いので、残しておきたい変数です。シミュレーション用のモデルとしては、ループを含む形が優れています。
◆ 2次遅れ近似モデルにおいて、さらに、インダクタンス L も十分に小さいという条件を入れると、より簡単な形の近似モデル図 6-1-24 が得られます。
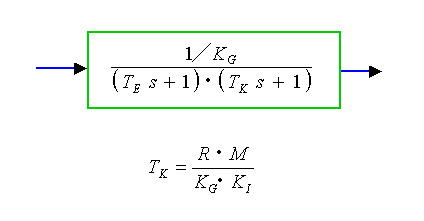
◆ これも 2 次遅れですが、2 つの 1 次遅れに分離された形になっています。
しかも 1 つは、図 6-1-18に示した電気的特性に等しくなります。
したがってこのモデルの、もう一方の 1 次遅れは、DC モータの機械的特性を近似していると考えられます。
このもう一方の 1 次遅れの時定数 Tk を、DC モータの機械的時定数 と呼んでいます。
インダクタンスが十分小さく、図 6-1-24 に示した近似が成立する条件は、
・・・・ (6-1-3)
です。この条件は、モータの機種によっては、必ずしも成立しません。
◆ モータは、負荷を接続して使用します。一般に、制御対象は、モータ単体ではなく、負荷が掛かっています(図 6-1-25)。
[図 6-1-25] 負荷が掛かったモータ
◆ 負荷は多種多様ですから、その特性は、色々です。
しかし、負荷とモータが一体となっていて、剛体と見なされる場合には、モデルの形は、モータ単体と同じであり、パラメータだけが異なります。
負荷の質量 ML (慣性モーメント JL )、モータの質量 MM (慣性モーメント JM )とすれば、合成の質量 M (慣性モーメント J)は、
M = ML + MM J = JL + JM
であり、単なる加算です。
減衰係数についても、同様に、加算となります。
この合成値を使用すれば、モータ単体と同じモデルを使用できます。
◆ モータは、変速機 を介して負荷に接続される場合があります(図 6-1-26)。
[図 6-1-26] 変速機を使用する
◆ 図は、ギアを使用した変速機の例です。角速度の比 1/n ( n > 1 なら減速、一般にモータ系では減速です) の変速機では、1 次側に加えられたトルク Mt は、2 次側では n Mt となります。
変速機では、1 次側を 2 次側に等価換算するか、または 2 次側を 1 次側に等価換算して、まとめて取り扱います。
モータ( 1 次側)と負荷( 2 次側)のときは、負荷をモータ側にまとめて、総合するのが便利です。
機械系においても、電気系と同様に、インピーダンスを考えることができます。これを機械インピーダンス といいます。
変速機は、インピーダンス変換装置です。電気系のインピーダンス変換装置は、トランスです。したがって変速機は、トランスと同様に考えることができます。電気系の技術者は、トランスを基にして考えると分かりやすいでしょう。
力 F またはトルク Mt は、電気の電圧 V に対応します。
速度 Ve または回転速度 ω は、電気の電流 I に対応します。
質量 M または慣性モーメント J は、電気のインダクタンス L に対応します。
減衰係数 Kv は、電気の抵抗 R に対応します。
◆ 電気系のインピーダンス Z は、Z = V / I です。同様に、機械系のインピーダンス Zm は、
Zm = F / Ve または、Zm = Mt / ω
です。
2 次側の機械インピーダンス Z2 は、1 次側に換算すると 1 / n2 になります。
2 次側の質量 M2 を 1 次側に換算する と、1 / n2 になります。
したがって、慣性モーメントについて、2 次側 J2 を 1 次側に換算して合成すると、
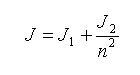・・・・(6-1-4)
となります。
なお変速機は、効率を考える必要がある場合があります。このときは、換算値に、動力伝達効率 η を掛ける必要があります。
◆ 以上、変速機について、解説しましたが、回転機器における変速機だけでなく、回転運動と直線運動を相互変換するラック/ピにオンや、直線的運動相互のリンク機構なども、同様に考えることができます。回転運動と直線運動の相互変換のときは、力とトルク等の変換になります。
