


◆ 伝送誤り の定義については、第 1 章の、コラム 1.3 に示しました。
伝送誤りの原因は、伝送波形の歪です。伝送波形は、伝送の途中で歪みます。歪みの原因は、既に説明してきたように、いろいろあります。外来ノイズによる歪みもありますし、伝送路の周波数特性、反射などもあります。
◆ ディジタル信号には、ノイズマージンがありますから、多少歪んでも、正しく伝わります。また、伝送用の IC は、シュミットトリガ特性を持っていますから、さらにノイズには強くなっています。
しかし、歪みが限界を超えれば、伝送誤りを引き起こします。
伝送誤りは、確率現象です。したがって、伝送誤り制御は、確率統計の立場から検討する必要があります。
◆ 波形歪みが、外来ノイズに起因しているときには、波形歪みと伝送とは、独立な要因です。したがって、伝送誤り発生の確率は、ランダムとなります。ランダムな誤りを、ランダム誤り と言います。
通常、伝送誤りは、ランダム誤りであるとして、論じられています。
◆ ランダム誤りにおいては、ある特定のビットが誤る確率は、そのシステムと、そのシステムが置かれている環境によって決まる、一定値です。
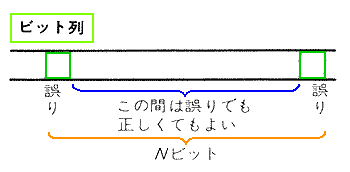
◆ しかし、伝送における誤りは、ランダム誤りだけではありません。複数ビットに跨るような、長時間連続するノイズの場合には、そのノイズが持続している、複数ビットの期間、データは、デタラメになるでしょう。デタラメであるということは、その間のあるビットは、間違っているかも知れませんし、偶然正しいかもしれません。このような誤りを、バースト誤り と言います(図.1)。
◆ 伝送誤りが、ランダム誤りであれば、伝送上の、ある任意の 1 ビットが誤る確率、ビット誤り率 は、一定です。その確率を、E とすれば、連続した 2 ビットのデータが誤る確率 E(2) は、
E(2) = E2
となります。ある特定の n ビット(連続であるとは限らない)が誤る確率 E(n) は、
E(n) = En
です。
◆ 伝送が実用になるためには、当然、
E ≪ 1
でなければなりません。したがって、連続した、または特定の複数ビットが共に誤る確率は、一つだけ誤る確率に比べて、はるかに小さく、無視することができます。
◆ バースト誤りは、上記の連続した、または特定の複数ビットのランラム誤りであるとして、計算した値よりも、はるかに高い確率で発生するものを言います。すなわち、バースト誤りは、それが発生する要因があって、発生する誤りです。
◆ 表.1 は、あるシステムにおける、バースト誤りの、実測例です。
| 誤りの種類 | 発生の割合 | ランダム誤りであるとしたときの発生割合 |
| 1 ビットの単一誤り | 50〜60% | 99.99% |
| 連続 2 ビットの誤り | 10〜20% | 0.001% |
| 連続 3 ビットの誤り | 3〜10% | 10-8 |
| 連続 4 ビットの誤り | 2〜6% | 10-13 |
| 4 ビット以上の誤り | 残 | - |
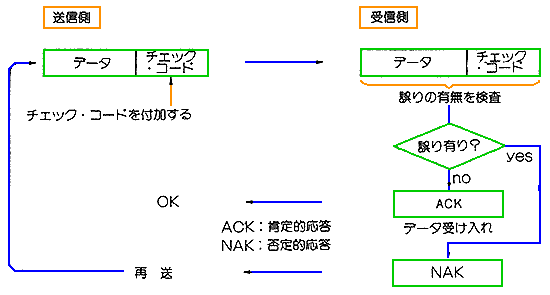
◆ 伝送誤り制御を行うためには、先ず、伝送誤りが発生したことを、検出する必要があります。伝送誤り発生を検出するためには、送信側で、伝送誤り検出用のチェックコード を、送信データに付け加えて送ります。受信側では、この送られてきたチェックコードを利用して、伝送誤りの有無を調べます(図.2)。
◆ 伝送誤りは、確率現象ですが、チェックコードで誤りを検出することもまた、確率現象です。すなわち、チェックコードによって、100% 伝送誤りを検出できるのではありません。
チェックコードで、誤り無しと判定したにも関わらず、実は誤っていたということが起こります。
これが誤り見逃しで、その確率を、誤り見逃し率 と言います。誤り見逃し率は、元になる伝送誤り率と、チェックコードの種類とによって異なります。
◆ チェックコードの検査能力は、誤り見逃し率によって評価します。これも、パリティチェック例にとって、説明します。さきに述べたように、特定の n ビットが誤る確率 E(n) は、Enです。
パリティチェックでは、奇数個の誤りは、全て検出可能ですが、偶数個の誤りは、誤り無しと判定してしまうので、検出することができません。
◆ したがって、誤り見逃し率 Em は、
Em = ΣE(2n) ≒ E(2) = E2
となります。一般に、誤り率 ≪ 1 ですから、近似解は、最小ベキ乗の項のみを考えれば、十分です。
◆ また、誤り率が小さければ、誤り見逃し率も小さいことが分かります。しかも、2 乗で効きますから、元になる誤り率が小さいことが有利です。
なお、誤り率も、誤り見逃し率も、m × 10n の n で評価すれば十分です。m の違いを考える必要はありません。
◆ バースト誤りでは、チェックコードの長さを N ビットとすれば、N の大きさが、問題になります。バースト誤りでは、N ビット以下の以下の長さのバースト誤りを、全て検出することができます。
N ビット以上の長さのバースト誤りに対しては、見逃しが発生しますが、N ガ大きいほど、誤り見逃し率は、小さくなります。すなわち、N ガ大きいことは、2 重に効いてきます(8.2.(4-A)参照)。
◆ チェックコードの評価は、基本的には、チェック能力ですが、その他、コードの長さ、コードの作りやすさ、チェックのし易さなどが、あります。コードが短くて、チェック能力が高ければ、理想的ですが、なかなか、そうは行きません。バースト誤りに対するチェック能力は、コード長さに依存します。
結局は、目的、用途によって使い分けることになります。
◆ 垂直パリティは、最も簡単で、その故に多く使用されていますが、チェック能力は低いのです。垂直パリティは、ランダム誤りに対しては、かなり強いのですが、バースト誤りに対しては、無力です。 なお、通常パリティと呼ばれているものは、垂直パリティ のことです(図.3)。パリティには、この他に、水平パリティがあります。

◆ 図中の式は、誤り見逃し率 Es で、E はビット誤り率です(以降の図も同様)。
垂直パリティは、本格的な、データ伝送では、バースト誤りがあり得ますから、使用できません。近距離のインターフェースに使われています。
近距離のインターフェースでは、伝送誤りは、事実上存在しません。むしろ、機器の電源の入れ忘れ、ハードウェアの故障などのチェックの意味を持っています。
◆ なお、垂直パリティが多く使われているのは、マイコンに内蔵されている、UART が、垂直パリティの機能を内蔵いることにも、よります。
ただし、UART がパリティ機能を持っていても、使わないことも多いのです。パリティビットを付加することによる、実効伝送速度の低下を嫌ったのでしょう。
◆ 水平パリティ は、最近では、ほとんど使われませんが、昔は、ベーシック手順で、広く使われた方式です(図.4)。
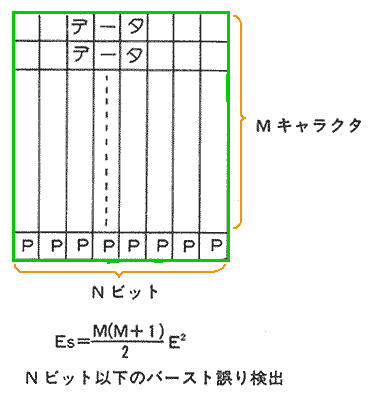
◆ 垂直パリティ、水平パリティの名前の由来ですが、この講座の垂直パリティの図、および水平パリティの図を 90 度回転すれば分かります。
水平パリティは、図から分かるように、複数キャラクタに対して、キャラクタを(この図では)縦断する方向にパリティを付けます。
キャラクタ数が多いと、上記の図の式から分かるように、誤り見逃し率は、急速に増加します。
水平パリティは、垂直パリティと異なり、バースト誤り検出能力があることが、特徴です。
◆ 水平パリティと似たものに、チェックサム があります(図.5)。
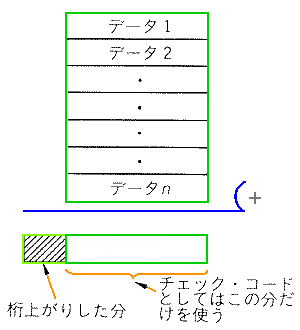
◆ チェックサムは、キャラクタを、四則演算の加算で足し込んだものです。
◆ 垂直+水平パリティ は、垂直パリティと、水平パリティとを併用した方式です(図.6)。
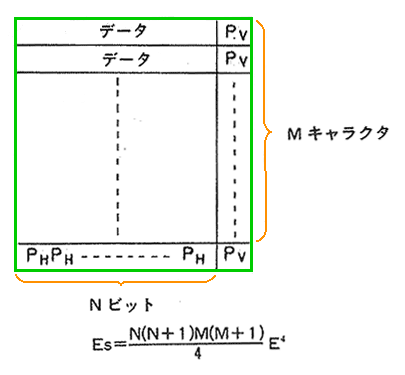
◆ 図の式から分かるように、誤り見逃し率が、E4 で効いてきますから、ランダム誤りに対しては、極めて強い方式です。バースト誤りについては、水平パリティと、ほぼ同様です。キャラクタは通常 7〜8 ビットですから、強いとは言えません。
昔は、この、垂直+水平パリティ方式が、最強の方式でした。しかし、最近では、高度な伝送では、キャラクタ単位の伝送それ自体が、減っていることもあって、あまり使われていません。