


◆ 2 連送照合 は、チェックコードとして、データ自身を使用します。すなわち、同じものを 2 回送ります。コードが長く、効率は良くありませんが、簡単なことが取り柄です。
データ自身が短いと、バースト誤りに弱くなります。キャラクタ単位の伝送であれば、複数キャラクタを、まとめて適用すれば、強くなります(図.7)。
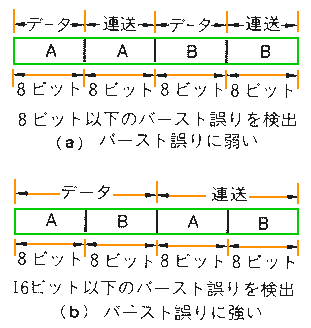
◆ 連送データを反転させる、反転 2 連送照合 も、あります。通常の直列伝送では、反転と非反転とでは、能力上の差はありません。しかし、並列伝送においては、反転させることによって、ハードの故障が検出可能になります(図.8)。
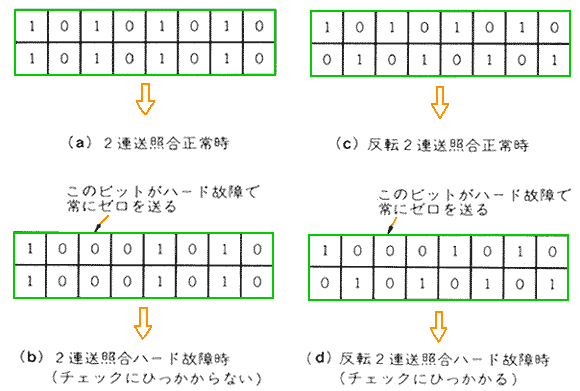
◆ 図の(b)に示すように、2 連送照合では、ハードが故障したとき、チェックに引っ掛かりません。しかし、反転 2 連送照合では、(d)のようになりますから、ハードの故障を検出することができます。
2 連送照合に類似のものに、返送照合 があります。送信側からは、チェックコード無しに、データだけを送ります。受信側では、この、受け取ったデータを、送信側に送り返します。送信側で、最初に送ったデータと、返送されてきたデータとを照合します(図.9)
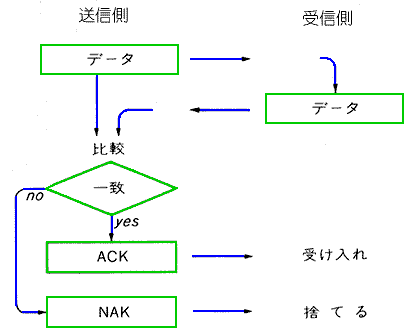
◆ 照合それ自体は、簡単であり、優れた方式のように思われますが、伝送誤り制御全体としての処理が複雑になります。したがって、あまり使われていません。
◆ CRC (3.3.コラム3.6 参照) は、サイクリック リダンダンシ チェック の略です。チェックコードとして、広く使われています。ただし、CRC は、分類的名称であり、CRC に属するコードは、多数あります。その中で、優れた特性を持つ、特定の、幾つかのコードを、CRC と通称しているのです。
CRC の定理 を、表.2 に示します。
| 定理 (1) | 2n ビット以下の誤りを検出できるなら、n ビット以下の誤りを訂正できる。 |
| 定理 (2) | 生成多項式の項数が、2 項以上であれば、単一誤りを、全て検出する。 |
| 定理 (3) | 生成多項式項数が偶数なら、奇数個の誤りを、全て検出する。 |
| 定理 (4) | a 次の生成多項式は、長さ a 以下のバースト誤りを、全て検出する。 |
| 定理 (5) | 長さ b = a + 1 のバースト誤りで、検出されない誤りの割合は、2-(a-1) である。 |
| 定理 (6) | 長さ b > a + 1 のバースト誤りで、検出されない誤りの割合は、2-a である。 |
| 定理 (7) |
その指数*1)が e である生成多項式は、そのメッセージ長さが n ≦ e ならば、 全ての単一誤り、2 重誤りを検出する。 |
| 定理 (8) |
P(x) = (1 + x)・P1(x1) を生成多項式とすれば、メッセージ長さ n が、 P1(x) の指数 e より大きくないならば、全ての単一、2 重誤りを検出する。 |
| 定理 (9) |
PX = (1 + X)・P1(x) を生成多項式とすれば、メッセージ長さ n が、 P1(x) の指数 e より大きくないならば、長さ 2 以下の 2 つのバースト誤りを検出する。 |
| 定理 (10) |
P(x) = (Xc + 1)・P1(x) を生成多項式とすれば、つぎの 3 つの条件のもとで、 2 つのバースト誤りのどんな組み合わせ E(x) = Xi・E1(x) + Xj・E2 をも検出する。 (a) C + 1 がバースト長さの和に等しいか大きい (b) G1(x) は素多項式*2)であり、短いほうのバースト長 b より小さくない次数である。 (c) メッセージ長さ n が G1(X) の指数 e と c の最小公倍数より大きくない。 |
◆ チェックコードには、誤りがあるかどうかを、検出できるだけでなく、誤りを訂正できる能力を持つものもあります。定理(1) は、誤り訂正能力に関する定理です。
垂直パリティは、生成多項式が、
P(x) = X + X0
の CRC です。定理(3)によって、奇数個の誤りを、全て検出できます。
垂直パリティは、誤り検出能力が高くありません(とくにバースト誤りに対して弱い)。CRC だと言うことが、即、優れてはいないという、証拠です。
◆ 水平パリティは、生成多項式が、
P(x) = Xm + X0
の CRC です。定理(4)によって、長さ m 以下のバースト誤りを全て検出することができます。
2 連送照合は、メッセージ長さとチェックコード長さが等しい 水平パリティと考えることができます。したがって、CRC に属します。
以上のように、従来使用されてきたチェックコードも、実は、CRC に属するコードです。
◆ 定理(4) によって、全てのチェックコードは、その長さ以下のバースト誤りは、全て検出できることが分かります。
また、定理(5)、(6) によって、チェックコードよりも長いバースト誤りであっても、チックコード長さが長いと、誤り見逃し率が小さくなります。
チェックコードが長いことは、バースト誤りに強いことを、意味します。
◆ 定理(7)〜(10) は、CRC の詳細な性能に関するものです。
チェックコードは、長い方が優れてますが、同じ長さでも、優劣があることが分かります。
◆ 従来から使われてきた、各種のチェックコードも、CRC に属します。しかし、CRC 独自のコードも多く使用されています。
(a) CRC-16 : 生成多項式が、
P(X) = X16 + X12 + X2 + 1
のものです。ベーッシック手順に属するバイシンクに使用されています。ただし、現在では、ベーシック手順そのものが、あまり使われていません。
◆ (b) CRC-CCITT : 生成多項式は、
P(X) = X16 + X12 + X5 + 1
です。ハイレベル手順に属する HDLC に使われています。全ての、単一および 2 ビットの連続ビット誤り、全ての奇数ビット誤り、16 ビット以下のバースト誤り、99.997% の 17 ビットバースト誤り、99.998% の 18 ビット以上のバースト誤り、を検出します。
◆ 以上のように、CRC は、16 ビットものが多く使われています。216 = 65536 です。「万が一」という言葉もあります。十分小さい、または十分少ないということが、実用上 10-4 程度を意味することが多いのでしょう。
◆ (c) LAN : イーサーネットでは、32 ビットの、CRC が使われています。イーサーネットは、当初、衝突が起こる方式が使われていました。衝突が発生すれば、衝突している期間の、極めて長いバースト誤りになります。これに対応するために、長いチェックコードを使用したのでしょう。定理(5)、定理(6) によって、チェックコード長さが、長いと誤り見逃し率が低くなります。誤り見逃し率は、2-32 ≒ 2.3 × 10-10 のオーダーです。
◆ CRC は、ソフトウェアなら簡単に、作成、チェックできます。ハードウェアも簡単な回路で実現できます(図.10)。
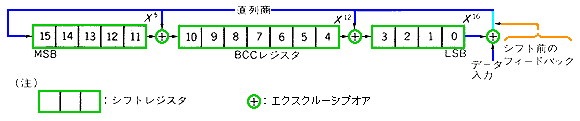
◆ CRC 自体の回路は簡単ですが、伝送誤り制御全体は、複雑です。CRC を用いた、伝送誤り制御を行うのであれば、CRC を内蔵している直列伝送用の LSI を使用するのが実用的です。HDLC は、CRC を使用していますから、それを利用するのが良いでしょう。
非同期式で、CRC を使いたいのであれば、ソフトウェアで、CRC をつけるのが実用的です。
◆ CRC の定理(1) からも分かるように、単に誤りの有無を検出するだけでなく、誤りを訂正することが可能なコードがあります。これを誤り訂正コード と言います。
誤り訂正ではなく、誤りを検出するチェックコードを使用して、誤り制御を行う場合は、図.2 に示したように、受信側で誤りを検出した場合には、NAK の返事を返して、データを再送してもらいます。
この方式を、誤り検出再送方式 といいます。
◆ これに対して、誤り訂正コードを使用すれば、受信側は、自分で誤りを訂正できますから、再送してもらう必要はありません。これを誤り検出訂正方式 と呼びます。返事すら必要ないとも考えられます。しかし、ACK/NAK の返事を貰わないと、不測の事態に、伝送がうまく進まない恐れがあります。誤り訂正コードを使用しても、一般には、返事が必要です。
◆ 返事は必要ですが、再送の必要がなくなる分、伝送効率が高くなります。ただし、誤り訂正コードは、誤り検出コードに比べて、同じ能力を持たせるためには、長さが 2 倍必要です(CRC 定理(1))。
結局、この兼ね合いで、どちらが得か、ということになります。
◆ 伝送誤り率自体が小さいシステムでは、再送回数が少ないので、通常は、検出再送方式の方が優れています。これに対して、伝送誤り率が多いシステムでは、誤り訂正方式一般に、有線の伝送では、伝送誤り率が小さので、検出再送方式が多く使用されています。これに対して、無線では、伝送誤り率が大きいシステムもあります。それらには、誤り訂正方式が使われています。
◆ 誤り訂正コードの代表的なものに、ハミング コード があります。ハミング コードは、1 ビットの誤りを訂正することができます。したがって、2 ビットの誤りを検出することができます(CRC 定理(1))。ハミング コードは、データとチェックコードとが入り混じっています。すなわち、文字コード自体が誤り訂正機能を持っています。
◆ コードには、ハミング距離 と言う概念があります(図.11)。
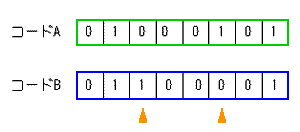
◆ 図で、コード A とコード B とでは、2 ビット異なっています。これを、ハミング距離が 2 であると言います。
伝送誤りによって、互いのコードが一致してしまうためには、図から明らかなように、ハミング距離だけのビット数を誤ることが必要です。すなわち、ハミング距離が大きいことは、伝送誤りに対する強さが強いことを表わしています。
◆ ハミングコードは、互いのハミング距離が、最大になるように作られたコードです。
具体的には、たとえば、8 ビットのネットデータを送るのに、12 ビットのコードを使用します。
◆ 2 out of 5 コードは、自己訂正コードでは、ありませんが、誤り検出能力を持つ、数字表現方法です(図.12)。
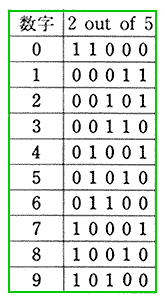
◆ 5 ビットのコードで、そのうち 2 ビットが 1 のコードです。同様にして、n out of m を作ることができます。
以前は、ハードウェアで、データを 10 進数で送ることが多かったので、よく使用されました。最近では、マイコンを使用するシステムが、ほとんどなので、あまり使われません。
★ CRC の理論的なベースになっているのが、符号理論と呼ばれる理論です。
★ 誤り検出や、誤り訂正を行うためには、その情報を表わすために必要なビット数 n に対して、誤り検出や、誤り訂正を行うために必要な情報を、k ビット付け加える必要があります。
★ この付け加える k ビットの情報を、冗長ビットと呼んでいます。
★ 冗長ビットは、誤り検出や、誤り訂正を行うために必要な情報ですから、決して無駄な情報ではないのですが、本来の情報を表わすための情報では無いと言う意味で、冗長の名がついています。
★ しかし、冗長ビットは、本来の情報に、付け加えなければならない、情報ですから、その効果は大きく、長さはできるだけ短いことが、望まれます。
これを実現するための理論が、符号理論です。
★ 誤り制御用の符号は、いろいろな立場から分類できます。
(1) 用途 : データ伝送、バーコード 等
(2) 機能 : 誤り検出符号、誤り訂正符号
(3) 誤りの種類の対象 : ランラム誤り、バースト誤り、バイト誤り
(4) 種類 :

★ 畳み込み符号とは、複数のブロックに依存する符号です。衛星通信などに使われています。
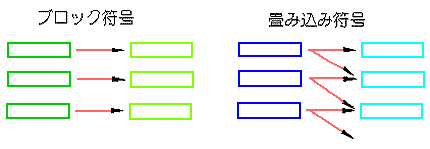
★ CRC は、巡回符号に属します。