


◆ 速度〜電流のカスケード制御 を、図 6-3-34 に示します。
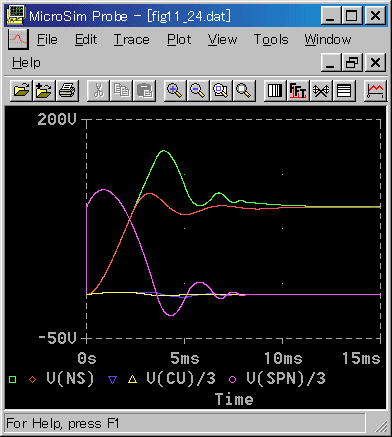
◆ SPN は、マイナーループの目標値です。
予想に反して、カスケード制御は、遅れが大きく、マイナス効果です。この原因は、マイナーループの目標値(メジャーループの出力値)にあります。
この目標値に対して、マイナーループは、追随することができません。これが、リセットワインドアップと同等の働きをしています。
対策として、メジャールーループの出力をリミットします。その結果が、図 6-3-35 です。
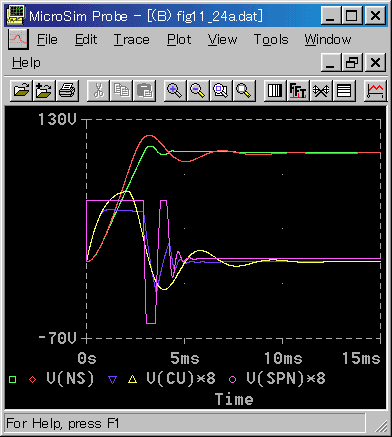
◆ 振動の周期が短くなったという意味では、応答は大幅に改善されています。しかし、最初の立ち上がりは、改善されていません。これは、電圧のリミットからくるもので、カスケード制御では、どうすることもできません。
カスケード制御は、高速の応答を実現します。高速応答を実現するためには、加速度が大きくなければなりません。大きな加速度は、大電流によって実現します。
大電流が可能なモータでなければ、カスケード制御の性能を、発揮することはできません。
シミュレーションですから、大きなモータを使用する代わりに、リミットを外して見ます(図 6-3-36)。
実際には、大きなモータを使用することになりますが、それだとモータの特性が変わってしまいます。シミュレーションでは、純粋にカスケード制御だけの効果を調べることができます。
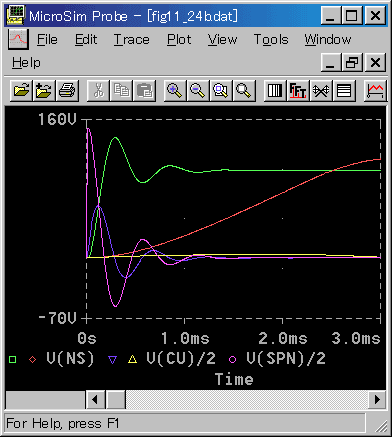
◆ これが、速度〜電流 カスケード制御の実力です。
また、現実の、電圧がリミットされたモータも、低速で使用すれば、高速応答が可能です(図 6-3-37)。
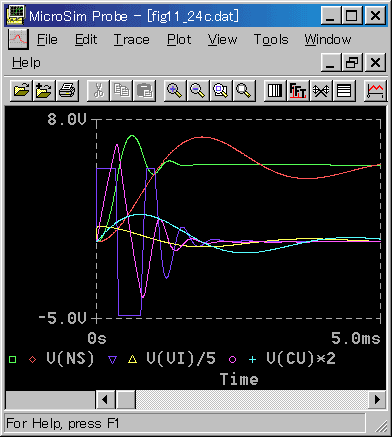
◆ 始めのところで、若干電圧 VI のリミットに引っ掛かっていますが、カスケード制御の性能は十分に出ています。
このモータは、減衰がありませんから、速度ゼロからのスタートアップでなく、ある速度で運転しているときに、目標値を小さなステップで変化させたときも、同様な応答になります。
台形制御も、ステップに比べて加速度が小さくて済みますから、実用になります(図 6-3-38)。
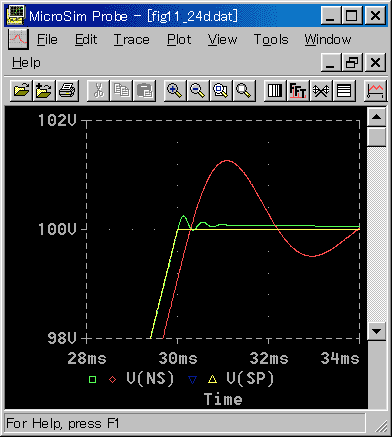
◆ 6.2.1.(3-D)の図 6-2-7と同じ台形制御を行ったものです。水平に移行する部分を拡大表示しています。
◆ しかし、カスケード制御も万能ではありません。
カスケード制御の効果は、制御対象の特性に依存します。
位置〜電流のカスケード制御 を示します(図 6-3-39)。
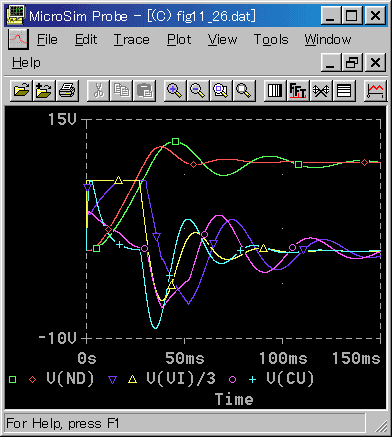
◆ 色々と条件を変えて見ても、カスケード無しに及びません。この原因はどこにあるのでしょうか。
電流値を見ると、ピークを作り急速に減少しています。この辺に原因がありそうです。しかし、カスケード無しも同様ですから、カスケード無しとの差は、説明できません。
そこで、電流 CU 入力に対する位置 ND と速度 NS のステップ応答を比較して見ることにします。
このモータ モデルでは、直接電流 CU を入力にすることができませんから、電流 CU の定値制御を行なって、そのときの位置 ND と速度 NS とを調べます(図 6-3-40)。
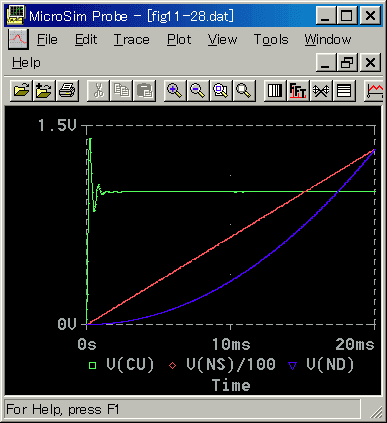
◆ 速度 NSは、電流に対して、速やかに立ちあがっています。したがって、マイナーコントローラによって電流 CU が速く変化すれば、速度 NS の応答も速くなると考えられます。
これに対して、位置 ND は、電流 CU が変化しても、ND 変化し始めるまでに時間が掛かります。したがって、マイナーコントローラによって、電流 CU の変化が速くなっても、位置 ND の変化速度にはあまり影響しないと思われます。
電流 CU〜位置 ND のカスケード制御の効果が無いのは、これが原因であると推定されます。
◆ 原因を確認するためにモデルを作って、実験して見ます。
入力が変化しても、遅れによって出力が変化しない典型的なモデルは、無駄時間を含む系です(3.1.3.(4-A))。
むだ時間が小さい制御対象をカスケード制御した場合と、むだ時間が大きな制御対処をカスケード制御した場合とを、比較して見ます。
制御対象モデルを、図 6-3-41 に示します。
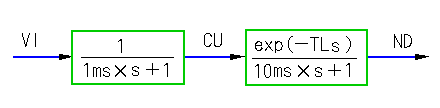
◆ むだ時間 TL は、むだ時間が小さい系が 0.5ms、むだ時間が大きい系が 10ms です。
このモデルをカスケード制御したときの制御応答を図 6-3-42、図 6-3-43 に示します。
[図 6-3-42] モデルのカスケード制御(むだ時間 0.5ms)
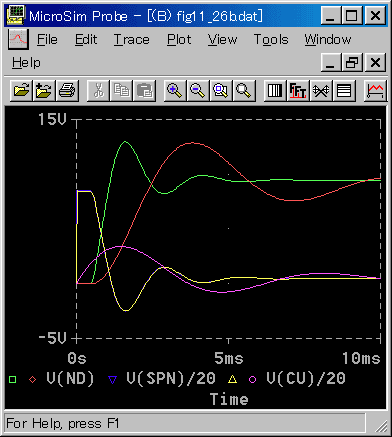
[図 6-3-43] モデルのカスケード制御(むだ時間 10ms)
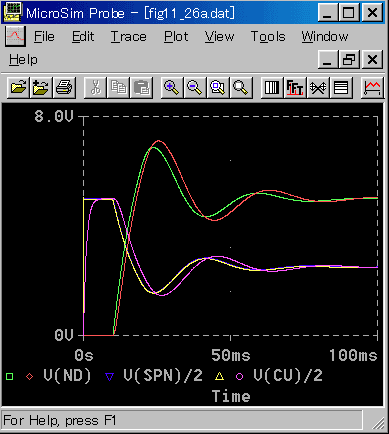
◆ 比較のために、カスケード無し を入れてあります。
全て P 動作で、比例ゲイン KP は、
むだ時間 0.5ms、メジャーループ : 17
むだ時間 0.5ms、マイナーループ : 100
むだ時間 0.5ms、カスケード無 : 10
むだ時間 10ms、 メジャーループ : 1
むだ時間 10ms、 マイナーループ : 100
むだ時間 10ms、 カスケード無 : 1
です。
むだ時間が小さい系では、カスケード制御が有効です。しかし、むだ時間が大きい系では、カスケード制御の効果がありません。
以上から、位置〜電流のカスケード制御は、効果が無いことが分かります。
[注] このように、極端な、典型的なケースをシミュレートすることによって、原因を探求できることも、シミュレーションの効用です。
◆ 位置〜速度のカスケード制御 は、どうでしょうか(図 6-3-44)。
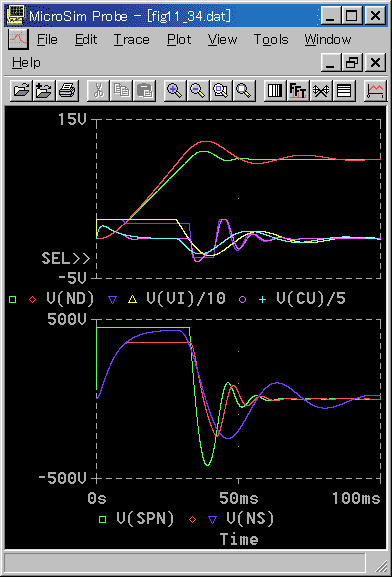
メジャー : KP = 500、TI = 100ms、出力リミッタ = ±450
マイナー : KP = 0.5
カスケード無 : KP = 13、TI = 25ms
です。
◆ 速度〜電流のときと同様に、メジャーループの出力にリミットをかけてあります(6.3.2.(2-C))。
最初の立ち上がりが、電圧でリミットされているのはやむを得ないことです。カスケード制御の効果は十分にあります。
◆ 位置制御の本命は、追値制御です。位置〜速度カスケード制御を、追値制御に使って見ましょう(図 6-3-45)。
[図 6-3-45] 位置ND〜速度ND カスケード制御(追値制御)
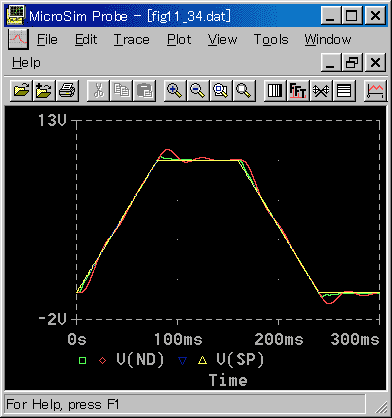
◆ 良く制御されています。立ち上がり時の詳細を、図 6-3-46 に示します。
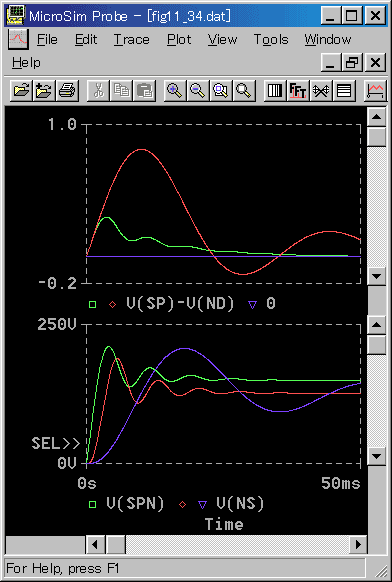
◆ さらに電流を加えた、位置〜速度〜電流の複合カスケード制御 (追値制御)を行います。 図 6-3-47 に最初の立ち上がり時を、図 6-3-48 に立ち上がりから水平への移行時を示します。
[図 6-3-47] 位置ND〜速度NS〜電流CU カスケード
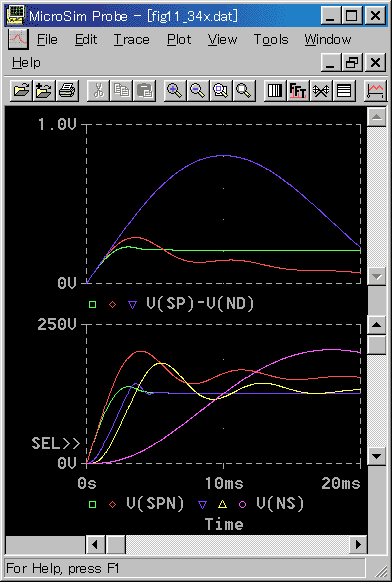
[図 6-3-48] 位置ND〜速度NS〜電流CU カスケード
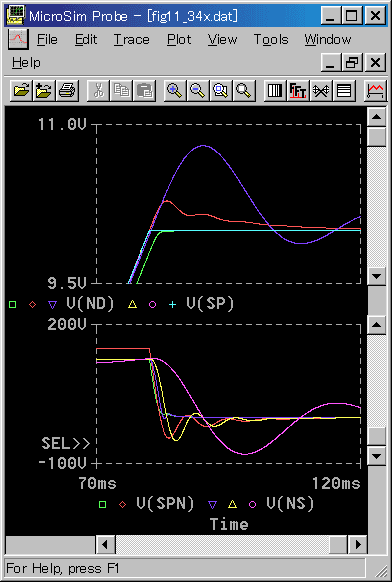
◆ また、サブマイナーループの応答は、図 6-3-49 のとおりです。
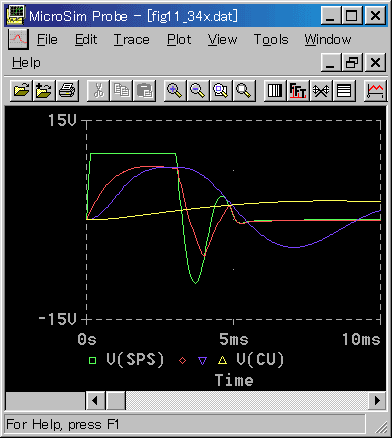
[注]
位置〜速度〜電流のカスケード制御は、シミュレーション エラーが発生します。そのため、ステップ応答を示すことができません。
また、追値制御においても、積分動作を十分に効かせることができません。したがって、PI 動作ではなく、P 動作の結果を示してあります。
◆ 図 6-3-47 の偏差 SP-ND は、P 動作なので、オフセットがあります。この点を除いては、応答は、大幅に速くなっています。
立ち上がりから水平に移行するときは、P 動作で、元の状態に戻るのに近い動作ですから、極めて速くなっています。積分動作が効いているときは、逆に、行き過ぎが発生して、定常に戻るのに時間が掛かるはずです。
◆ モータ制御の場合は、カスケード制御に期待する効果は、追値制御に対する応答性の向上が主体です。
しかし、外乱に対する効果も十分あり、期待することができます。
位置〜速度カスケードの例を示します(図 6-3-50)。外乱はトルクです。
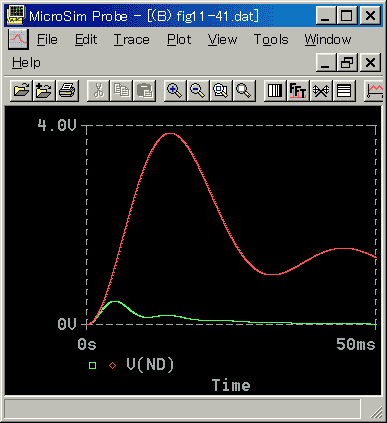
◆ 比較の対象は、カスケード無しです。
外乱に対しても大きな効果があることが分かります。
◆ 外乱に対するカスケード制御は、主に、定値制御が多いプロセス制御で使用されます。
外乱に対するカスケード制御の効果は、外乱の入力点によって異なります。
これを調べるために、図 6-3-51 の制御対象モデルを考えます。
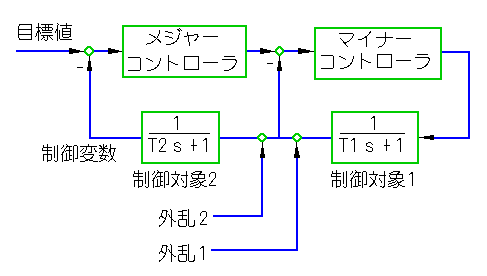
◆ このモデルは、外乱の入力点による制御応答の違いを調べるためのモデルであり、実在の制御対象を想定したものではありません。
図において、外乱1はマイナーループの中に、外乱2はマイナーループの外に加わります。その他の違いはありません。
制御対象の特性は、共に1次遅れとします。
まず、制御対象の特性が、マイナー側 T1=3ms、メジャー側 T2=10ms 、すなわち、マイナー側の応答の方が速いときのときを図 6-3-52に示します。
[図 6-3-52] 外乱に対する効果(マイナー側が速いとき)
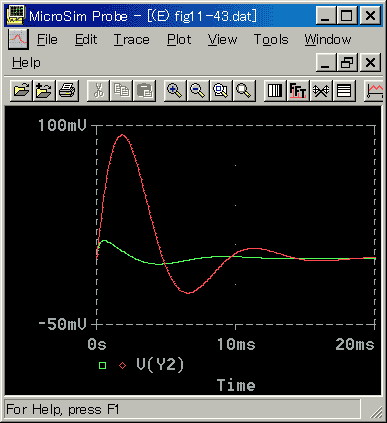
◆ 外乱が、マイナーループの中に加わるときの方が、外乱が良く打ち消されています。
次に、マイナー側 T1=10ms、メジャー側 3ms、すなわちメジャー側の応答の方が速いときを図 6-3-53 に示します。
[図 6-3-53] 外乱に対する効果(メジャー側が速いとき)
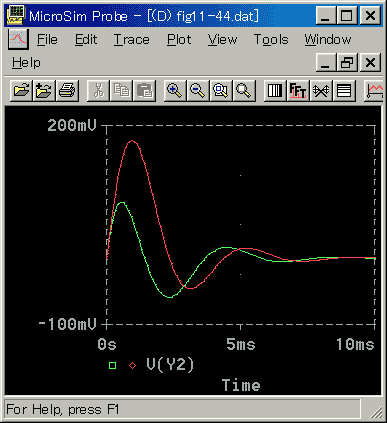
◆ 外乱がマイナーループの中に加わる方が、成績が良いことには、変わりありませんが、その差が少なく、かつ偏差の絶対値が大きくなっています。
以上から、外乱に対するカスケード制御の効果は、
制御対象の特性が、マイナーが、メジャーに比べて速く、外乱がマイナーの内部に加わるとき、最も効果が大きく、
制御対象の特性が、マイナーが、メジャーに比べて遅く、外乱がマイナーの外側に加わるときは、効果が小さい、
ことになります。
★ 定値制御の本来の目的は、制御変数の値を、できるだけ一定にすることにあります。しかし、ときには、自動制御しているにも関わらず、あまり一定にしない方が良い場合があります。
制御対象は、システムです。ある制御を行った結果が、他の制御変数に対して外乱となることがあります。
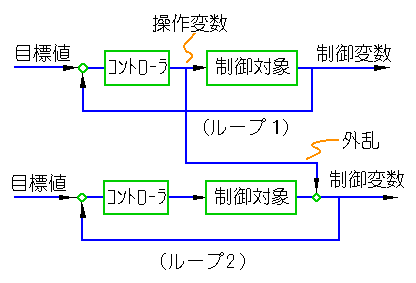
★ 具体例として、下記のようなプロセスがあります。
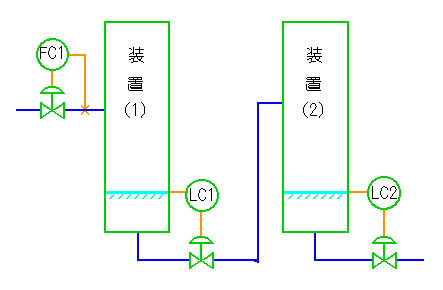
★ 化学プロセスでは、図のように、原料が各装置を次々と通過し、それぞれの装置で加工されて行きます。
各装置は、できるだけ安定した操業が要求されます。そのためには、先ず各装置への、装入流量を 1 定にすることが重要です。最初の装置(1) は、流量の自動制御 FC1 で一定に保たれます。
★ 各装置では、底に液がたまり、液面ができます。この液面は、コラム 6-2-3 で述べた理由によって、液面制御が必要です。装置(1) の液面は、LC1 によって制御されます。
この LC1 の外乱は装置内で落下してくる液流量で、操作変数は装置(1) の抜き出し流量( = 装置(2) へ装入流量)です。
★ LC1 が働くことによって、装置(1)の液面は制御されますが、その操作変数である、装置(2)への装入流量は、変動します。これは、装置(2) に取っては外乱となります。
まさに「こちらを立てれば、あちらが立たず」です。
そこで、考え出されたのが、流量〜液面のカスケード制御です。
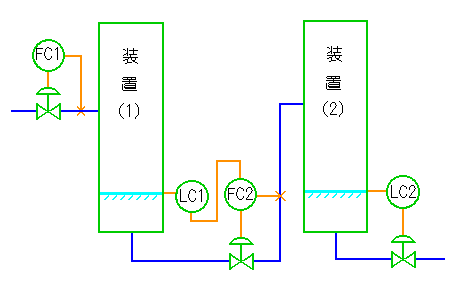
★ FC2 を加えることによって、装置(2)への流量も制御されます。ただし、流量は、カスケード制御のマイナーループです。マイナーループの役割は、メジャーループの制御性を高めることであった筈です。
メジャーループからの出力によって、FC2 の目標値が変化し、したがって流量は変動してしまいます。「なんだ、ぬか喜びだったのか」ということになります。
★ ところが、ここに奥の手があります。「均流液面制御 」と呼ばれる制御方式です。均流液面制御では、LC1 の制御パラメータの値を故意に、ぐんと緩くします。液面は外乱によってかなり変動します。
しかし、このような場所の液面制御系は、液面を厳密に一定に抑えることではありません。液面制御の目的は、液面自体が持つ無定位性を無くすことです。液面の変動はかなりあっても差し支えありません(コラム 6-2-3 参照)。
★ この均流液面制御は、自動制御における、一方の極端な例です。そして、これに対する、もう一方の極が、他を意に介さないで、その制御ループだけを考えて、ひたすら、制御変数の一定性を追及する制御です。
一般に、自動制御は、この後者だけを目的とするかのように、考えられています。しかし、均流液面制御とまでは行かなくても、その中間が最適である場合が存在します。
★ 制御対象は、複雑なシステムを構成しています(3.2.3.(3))。さきに、制御演算における、パラメータの独立性を論じました(3.2.4.(4-C))。制御演算式という簡単なものだから、独立性も容易に得られます。
しかし、複雑なシステムでは、独立性を得ることは、容易ではありません。相互に干渉がある方が普通です。
★ 「あちらを立てれば、こちらが立たない」中で、総合的に評価して、良く言えば全体のバランスを取る、悪く言えば妥協する必要があります。