4.　デ ィ ジ タ ル 制 御

4.2　ディジタル PID 制御

4.2.6.　サンプリング周期を決める

4.2.6.(1)　2 つのフェイズがある

◆　既に見てきたように、ディジタル制御では、サンプリング周期が、制御応答に大きな影響を及ぼします。したがって、サンプリング周期をどうやって決めるかが、問題になります。
このサンプリング周期の検討は、2 つのフェイズがあります。
1 つは、システム設計段階での検討です。とくに、高速応答が要求され、サンプリング周期を非常に短くする必要がある場合には、ハードウェア・コストとの兼ね合いがあり、この段階での検討が必要になります。
通常のコントローラでは、サンプリング周期は、制御パラメータの 1 つとして、可変になっています。この場合には、可変できる最小のサンプリング周期決定の、問題になります。
もう一つのフェイズは、実際に制御するに当って、制御パラメータとしての、サンプリング周期の決定です。

4.2.6.(2)　簡　便　法

◆　この簡便法は、実際に制御する場合に適用されます。
制御パラメータとしての、サンプリング周期を決める、最も簡単な方法は、サンプリング周期を変えて見ることです。

4.2.6.(2-A)　フィルタを含む式のとき

◆　実用式など、制御演算式がフィルタを含む場合は、サンプリング周期が短すぎることが障害になることはありません。
先ず、そのコントローラで設定可能な、最小のサンプリング周期を選んで見ます。制御対象の特性に対して、コントローラが、十分短いサンプリング周期を持っているなら、アナログと同等な制御成績が得られる筈です。
これを確かめるには、サンプリング周期を変えて見ます。サンプリング周期を変えても、制御成績が変わらないときは、アナログと同等と考えられます。
もし、アナログと同等の制御成績が得られなかったとしても、そのコントローラとしての能力の限界ですから、あきらめるしかありません。さらに良い制御成績を望むなら、サンプリング周期の速いコントローラに取り替えることになります。

4.2.6.(2-B)　フィルタを含まない式のとき

◆　基本式など、制御演算式がフィルタを含まない式で、微分動作を使用しているときは、サンプリング周期が過小なために、ノイズによる悪影響が現われることがあります。
微分動作を使用しないときは、フィルタを含む式と同じ取り扱いにします。
制御対象によって、ノイズの多い、少ないは、大幅に異なります。
ノイズが少ない系では、ノイズによる悪影響が出なければ、フィルタを含む式に準じることができます。
ノイズが無視できない系では、微分時間 TD と、サンプリング周期 TS とを、連動させる方式があります。
サンプリングは、フィルタの効果をもちます。4.2.3.(3-A) に示したように、TD / TS = 20 のとき、アナログと同等です。したがって、この比で連動可能な範囲では、連動させます。

4.2.6.(3)　アナログと同等な制御成績を得る

◆　PID制御においては、ディジタル制御の制御成績は、高々アナログと同等です。したがって、サンプリング周期を決める第一の目安は、アナログと同等な制御成績が得られる、サンプリング周期を見出すことです。
これは、システム設計段階、実際の使用、どちらにも言えることです。
基本式など、制御演算式がフィルタを含まない式では、最適なサンプリング周期が存在します。しかし一般にコントローラのサンプリン周期は可変ですから、システム設計段階では、余裕をとった短かめのサンプリング周期を見出せば十分です。
実用式など、フィルタを含む式では、サンプリング周期は短いほどアナログに近くなります。したがって、実用上アナログと同等と見なせる範囲で、できるだ長いサンプリング周期を見出すことになります。

4.2.6.(3-A)　安定限界から求める

◆　アナログと同等の制御成績を得るための、サンプリング周期は、安定限界の周波数 fs から求めることができます。
システム設計段階では、周波数応答を定量的に求めることが困難な場合が多いでしょう。しかし、安定限界の周波数の概略値なら、予想できることも多いと思われます。
限界感度法で最適調整された結果は、アナログ PID 制御の場合、微分時間 TD は、限界周期 TU に対して、
　 　TD = 0.125 TU
です(3.3.2.(2-F))。
そしてサンプリング周期 TS は、微分時間 TD に対して、時間領域形では、1/20 が最適値です。周波数領域形においては、十分にアナログに近いのは 1/50 程度ですが、1/20 でも、実用上はアナログに近いと見なすことができます。
◆　以上の結果をまとめると、

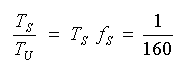　 　 　 ・・・・ (4-2-3)

が得られます。なお、この値は、次回出力です。同時出力なら、1 /80 です。

4.2.6.(3-B)　制御対象のむだ時間から求める

◆　制御対象の特性は、1 次遅れ + むだ時間 で近似すことができます(3.3.3.(1))。このむだ時間から、サンプリング周期を、求めることもできます。
制御対象を 1 次遅れ+むだ時間(TM)で表わしたとき、その限界周波数 fs は、その 1 次遅れ時定数 T にはあまり依存しないで、ほぼ無駄時間 TM によって決まります(図 4-2-41)。

[図 4-2-41]　1 次遅れ + むだ時間の周波数応答(TM = 1)

(図の上側の)緑から順に　T: 0.0001、0.001、0.1、1、10、100、1000

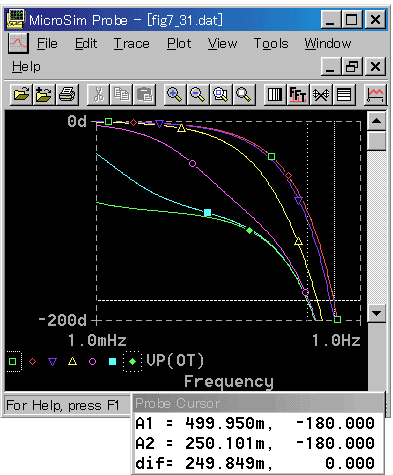
◆　時定数がゼロから無限大に変化しても、限界周波数 fs の値は、0.25〜0.5 / TM の非常に狭い範囲に収まります。このことから、

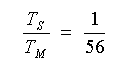　 　 　 ・・・・ (4-2-4)

を導くことができます。これも、次回出力です。

4.2.6.(4)　サンプリング周期を長く取る

◆　コントローラのサンプリング周期は、コントローラのハードウェアによって制約されます。アナログに比べて制御成績を多少落しても良いから、なるべくサンプリング周期を長く取りたいという要求が発生する場合があります。
または、逆に、やむを得ずサンプリング周期が長くなってしまうのだが、制御成績が、どの程度悪くなるのかを、知りたいということがあります。
制御成績の絶対値を検討する必要があるときは、予め制御対象の特性を定量的に正確に把握して、シミュレーションなどによって、制御応答を具体的に検討しなければなりません。
しかし、制御成績をアナログ制御に対する相対値で評価すれば良いなら、すなわち、アナログ制御に比べて、評価関数の値が、どの程度落ちるか、ということであれば、簡単に求めることができます。
◆　ディジタル制御の制御成績(評価関数) Id を、アナログ制御の制御成績(評価関数) Ia に対する倍率で表した (Id / Ia) と、サンプリング周期 TS にたいする限界周期 TU の倍率 (TS / TU) との関係を、図 4-2-42に示します。

[図 4-2-42]　制御成績と、サンプリング周期の関係

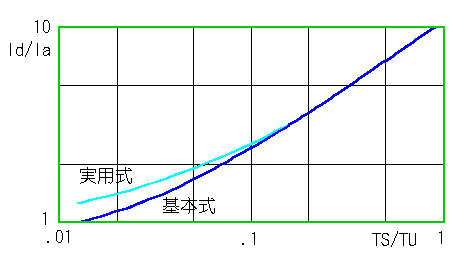
◆　ただし、この図は、標準 K の制御対象について、求めたものです。制御対象が異なれば、値は変わります。したがって、ごく大雑把な目安として使用してください。
図で、左端の値は、基本式で、特性がアナログと一致する、TD / TS = 20 の条件です。この条件では、実用式は、アナログよりも劣ります。
また、この図から、アナログに比べて、評価関数を 2 倍にすれば、サンプリング周期は、4〜5 倍に取れることが分かります。
◆　参考として、図 4-2-42 を作成するベースとした、最適応答(行過ぎ有)を、図 4-2-43〜図 4-2-46 に、その条件を表 4-2-5 示します。

[図 4-2-43]　最適応答(基本式)

緑から順に アナログ、TS = 34m、70m

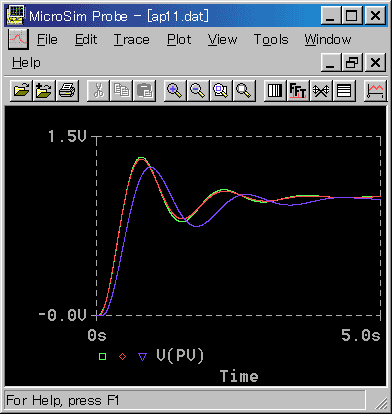
[図 4-2-44]　最適応答(基本式 その 2)

緑から順に TS = 200m、500m、1000m、2000m

[図 4-2-45]　最適応答(実用式)

緑から順に アナログ、TS = 30m、70m

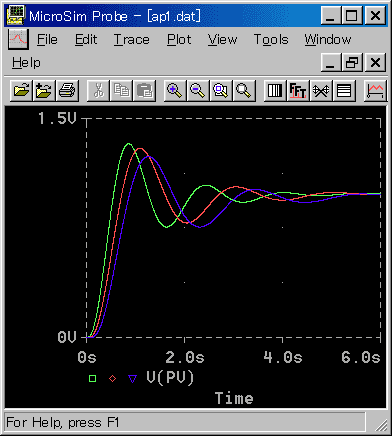
[図 4-2-46]　最適応答(基本式)

緑から順に TS = 200m、500m、1000m、2000m

[表 4-2-5]　最適応答時の条件