宮崎技術研究所自動制御講座 4.1.1.アナログ制御とディジタル制御

◆　Z 変換、したがってパルス伝達関数は、PSPICE で容易にシミュレーションを行うことができます。すなわち、Z 変換の z は、元々はラプラス変換です。
したがって、式 4-1-12 によって、パルス伝達関数を元の伝達関数形にすれば、直ちにシミュレーションを行なうことができます。
この伝達関数は、図 4-1-17 における y* ですから、アナログ系です。これをディジタル系にするには、サンプリングする必要があります。
しかしシミュレーションの上で、単に波形を見るだけなら、サンプリングを行なう必要はありません。シミュレーションの図を読むときに、アナログの連続した線の上で、サンプリング時点の値を読み取れば良いわけです。
通常サンプリングのタイミングは、図上でよく分かります。なお、ディジタル系をシミュレートしたのですから、サンプリングの中間の時刻における値は意味を持っていません。

4.1.3.(3-B)　具　体　例

4.1.3.(3-B-a)　微　　分

◆　簡単な具体例として、まず微分のパルス伝達関数を求め、それをシミュレートして見ます。同時出力形のパルス伝達関数は、式 4-1-20 です。これを式 4-1-12 で伝達関数に変換し、そのステップ応答を求めます。
回路ファイルはfg4_1_19.cirです(リスト4-1-1)。


　* (2) 引き算形
　.TRAN   1U  4M
　.PARAM  TS=1M
　VP  IN  0  PULSE(0, 1)
　E1  1   0  LAPLACE {V(IN)} = {EXP(-TS*S)}
　E2  OT  0  VALUE = {(V(IN)-V(1))/TS}
　.PROBE
　.END
　* (1) 直接形
　.TRAN   1U  4M
　.PARAM  TS=1M
　VP  IN  0  PULSE(0,1)
　E1  OT  0  LAPLACE {V(IN)} = {(1-EXP(-TS*S))/TS}　
　.PROBE
　.END
　* (3) アナログ
　.TRAN   1U 4M
　.PARAM  TS=1M
　VP  IN  0  PULSE(0, 1)
　E1  OT  0  LAPLACE {V(IN)} = {S/(1+TS*S)}
　.PROBE
　.END

[注]　このリストには、独立した回路が複数入っています。これについては、2.2.7.(2)に解説してあります。

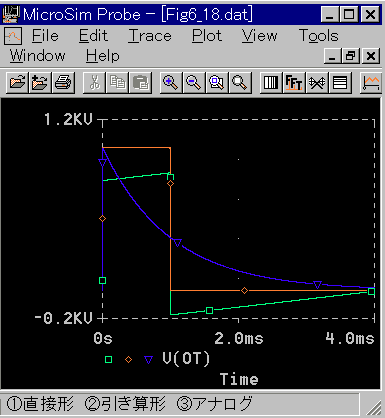
(1) の直接形は、警告が出て、波形が大きく歪んでいます。直接形は、元のパルス伝達関数を、そのままラプラス変換形に直したものです。
(2) の引き算形は、正しい結果が得られるように、直接形を、変形したものです。正しい結果を得るためには、このような工夫が必要です。
(3) のアナログは、比較のための、アナログ微分(実用)です。

◆　図の波形は、結果的にサンプル値をホールドした波形になっています。これは、ステップ応答の入力波形が一定値であるために、サンプリング時点間の波形が水平になったのであって、本当にホールドしたのではありません。
ですが、この図を利用して説明します。
ディジタル微分のステップ応答は、最初の 1 サンプル目に高さ( １/θ )のパルスが出て、それ以外はゼロになります。これをホールドすると、図のように、1 サンプリング周期の幅のパルスになります。その面積は 1 です。
真のアナログ微分のステップ応答は、パルス幅がゼロ、パルス高さが∞で、その面積が 1 のパルスです。これは、実用になりませんし、シミュレーションもできません。
実用されている、フィルタ付きの微分を入れてあります(3.1.3.(5-B-b))。このパルスの面積も 1 です。
ディジタル微分(ホールド出力）は、フィルタが入っていませんが、フィルタ付の実用アナログ微分に近いことが分かります。サンプリングとホールドを行ったことが、アナログにおける、フィルタと同様な効果をもっていると、考えられます。

◆　次回出力形は、この微分に限らず一般に、同時出力形 G(z) に対して１サンプリング周期だけ遅れるのですから、

で与えられます。ステップ応答も 1 サンプリング周期づつ遅れた波形になります。

★　このケーススタディは、シミュレーションに興味のある人が行なって下さい。
次回出力形の微分の回路ファイルを作り、実行してください

4.1.3.(3-B-b)　積　　分

◆　積分の同時出力形のパルス伝達関数は、式 4-1-17、式 4-1-18 の 2 種類あります。式 4-1-17 に対応するステップ応答の回路ファイル(fg4_1_20.cir)を、リスト 4-1-2 に示します。


　* (1) 直接形
　.TRAN   1U  4M
　.PARAM  S=1M
　VP  IN  0  PULSE(0, 1)
　E1  OT  0  LAPLACE {V(IN)} = {TS/(1-EXP(-TS*S))}　
　.PROBE
　.END
　* (2) フィードバック形
　.TRAN   1U  4M  UIC
　.PARAM  TS=1M
　VP  IN  0  PULSE(0, 1)
　E1  1   0  LAPLACE {V(OT)} = {EXP(-TS*S)}
　E2  OT  0  VALUE = {TS*V(IN)+V(1)}
　.PROBE
　.END
　* (3) アナログ
　.TRAN   1U  4M
　VP  IN  0  PULSE(0, 1)
　E1  OT  0  LAPLACE {V(IN)} = {1/S}
　.PROBE
　.END

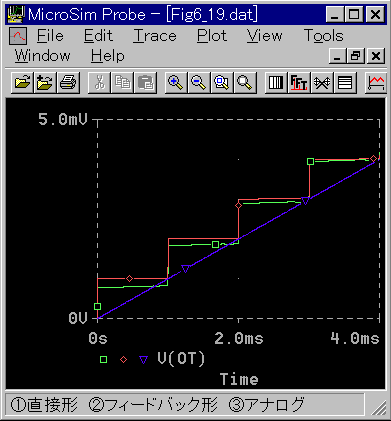
◆　これも微分と同様に、(1) の直接形は、警告が出て、波形が大きく歪んでいます。フィードバック形は正しい解が得られるように、直接形を変形したものです。
フィードバック形への変形は、ブロック図の変形法則 3.1.1(6-C) 図 3-1-11 の (16) で、F1(s)=1 と置いたものです。ただし係数を掛けるために、デバイス E2 の V(IN) のところに、TS を掛けてあります。
ディジタル積分をホールドすると、図のように、サンプル周期の幅を持つ階段状の波形になります。その傾斜はアナログと一致しています。
◆　式 4-1-18 に対応するステップ応答の回路ファイル(fg4_1_21.cir)のリスト 4-1-3 を示します。


* (1) フィードバック形
.TRAN   1U  4M
.PARAM  TS=1M
VP  IN  0  PULSE (0,1) 
E1  1   0  LAPLACE {V(IN)} = {EXP(-TS*S)}
E2  2   0  LAPLACE {V(OT)} = {EXP(-TS*S)}
E3  OT  0  VALUE = {0.5*TS*(V(IN)+V(1))+V(3)}
R1  2   3  1K
R2  3   0  1G
.PROBE
.END 
* (2) アナログ
.TRAN   1U  4M
VP  IN  0  PULSE(0, 1)
E1  OT  0  LAPLACE {V(IN)} = {1/S}
.PROBE
.END

◆　直接形は誤差が大きいので入れてありません。ステップ応答は 図4-1-21 です。

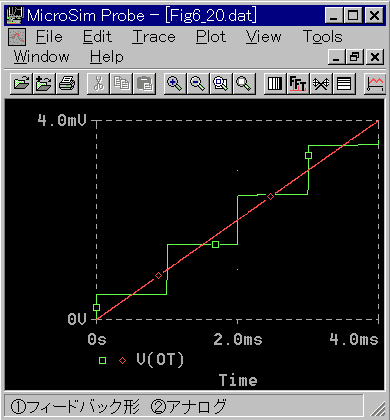
◆　図 4-1-20 の応答と比べて、ディジタルのジグザグがアナログの応答に対して振り分けになっています。この方が、より、アナログに近いと考えられます。さらに具体的には、後に、周波数応答で、説明します。

★　ディジタル微分とディジタル積分について、サンプリング周期を変えて、ケーススタディしてください。

★　このケーススタディは、シミュレーションに興味がある人が行なってください。
ステップ応答では、結果としてサンプルアンドホールドした波形と一致しています。一般には、そうならないことを確かめて見ましょう。
★　これはリストの電圧源デバイス VP のパルス波形を、ステップ波形から他の波系に変えれば良いわけです。たとえば、PULSE(0,1) を PULSE(0,1,0,4M) に変えればランプ波形(一定速度で増加する波形)になります。

4.1.3.(3-C)　サンプルアンドホールド

4.1.3.(3-C-a)　サンプルアンドホールドが必要

◆　シミュレーションの図を見るだけであれば、ディジタル系の波形も、伝達関数によるアナログ系のままでも、差支えありません。
しかし、アナログの制御対象と組み合わせて制御系を作るときなどは、ちゃんとした、ディジタル系に直す必要があります。
図 4-1-17 に示したように、アナログ系 ( y* ) をサンプリングすれば良いわけです。
実際の制御系では、アナログ入力をサンプリングしてディジタル化し、それをディジタル演算します。
シミュレーションの上では逆に、アナログ演算してから、後でサンプリングすることになります。
サンプリングした結果は、飛び飛びの瞬間的な値です。ディジタル系の出力は、一般にその後で D/A 変換、すなわちホールドします(図 4-1-22)。

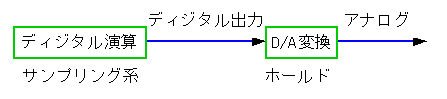
◆　したがって、シミュレーションでは、単にサンプリングするよりも、その後のホールドと組みあわせて、サンプルアンドホールド の形にまとめた方が、より一般的です(図 4-1-23)。

4.1.3.(3-C-b)　サブサーキット

◆　実際に使用されている、サンプルアンドホールドの回路を、図 4-1-24 に示します。

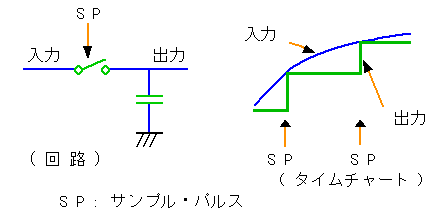
◆　スイッチをオンにすれば、コンデンサの電圧は、入力電圧に等しくなります。スイッチをオフにすれば、コンデンサの電圧は、スイッチをオフする直前の電圧を保ちます。
スイッチを、図に示すように、極めて短時間の、サンプル・パルス SP のタイミングだけオンにすれば、出力電圧は、図のタイムチャートのようになり、サンプルアンドホールドを実現します。
サンプルアンドホールドのサブサーキット SAH は、ほぼ、この回路どおりに構成されています。リスト4-1-4に示します。

*           出力 入力    サンプル周期    サンプル遅延(0～1)
.SUBCKT  SAH  OT  IN  PARAMS: TS=1M            DLY=0
 S21  IN  26  27  0  SHMD  ; ホールド・スイッチ
.MODEL SHMD VSWITCH VON=0.6 VOFF=0.4 RON=0.1 ROFF=10MEG
C21   26  0  {10U*TS}  ; ホールド・コンデンサ
ECNT  OT  0  26  0  1  ; 出力バッファ
V21 27 0 PULSE (0,1,{DLY*TS},{5M*TS},{5M*TS},{5M*TS},{TS})
+ ; ホールド パルス
.ENDS

(a)　サブサーキットの PARAMS: に、サンプル遅延 DLY があります。サンプルアンドホールドは、本来、そのディジタル系のサンプリングのタイミングで行います。
このサンプル遅延 DLY は、サンプリングのタイミングを、それより、ずらすためのものです。DLY は、0～1が、サンプル周期 0～100% に対応します。
DLY は、1 を超えることができます。このとき、最初のサンプルパルスが遅くなるだけで、以降はサンプル周期毎にサンプルされます。
(b)　V21 は、サンプルパルスを作る電圧源です(2.1.5.(2-E-c))。

◆　この DLY の用途は、2 つあります。1 つは、誤差防止です。この誤差は、ステップ状に急変している波形をサンプリングするときに、発生する可能性があります。SPICE は、アナログシミュレータなので、波形が鈍ることがあるからです(図 4-1-25)。

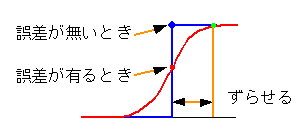
◆　図に示すように、ずらせることによって、この誤差を防ぎます。この措置によって、タイミングの誤差が発生します。しかし、波形の鈍りは、サンプル周期に比べて十分小さい筈ですから、タイミング誤差は軽微です。
もう 1 つの用途は、中間出力形に利用することです。これは、次の(3-C-c)で説明します。

サンプルアンドホールドの波形例を、図 4-1-26 に示します。

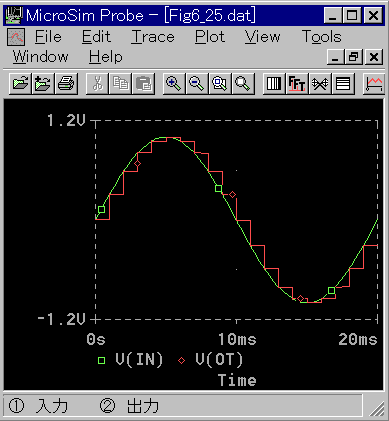
[注]　このように、サンプリングの対象が、連続的に変化している場合には、図 4-1-25 に示したような誤差は、発生しません。

4.1.3.(3-C-c)　中間出力形の出力

◆　理論上は、中間出力形は面倒です。しかしシミュレーションでは、サンプルアンドホールドによって、中間出力形を簡単に実現することができます(図 4-1-27)。

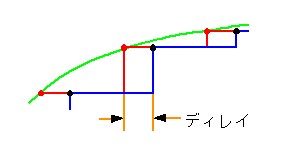
◆　サンプルアンドホールドを 2 回行ないます。1 回目(図の赤色)は、普通のサンプルアンドホールドです。2 回目のサンプルアンドホールド(図の黒色)は、一回目のサンプルアンドホールドの出力に対して行ないます。
この 2 回目のサンプルアンドホールドは、システムのサンプリング時点、すなわち 1 回目のサンプリング時点に対して、一定のディレイを設けてサンプリングします。
中間出力形出力 は、サブサーキットディレイアンドホールド DAHT になっています。書式は、

　*        操作出力  入力    サンプル周期 ディレイ(0～1) サンプル遅延(0～1)
　.SUBCKT DAHT  CNOT  IN  PARAMS:  TS=1M    TL=0        DLY=0.1

4.　ディジタル制御

4.1　ディジタル制御の基礎

4.1.3.　Z 変換とパルス伝達関数

4.1.3.(3)　シミュレーション

4.1.3.(3-A)　伝達関数を利用する